|| 積分の計算についてのまとめ
定義から導かれる計算について解説
スポンサーリンク
これはほぼ「微分法則」が元になってるので
これを理解せずに積分の計算を理解するのは
\begin{array}{llllll} \displaystyle \frac{dF(x)}{dx}&=&f(x) \end{array}
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x) \,dx&=&\displaystyle F(b)-F(a) \end{array}
「区分求積法」以外は無理だと思ってください。
\begin{array}{cccllll} t&=&g(x) \\ \\ \displaystyle g^{-1}(t)&=&x\end{array}
\begin{array}{rcrllllll} \displaystyle \int f(x) \,dx &=&\displaystyle \int f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \\ \\ \displaystyle \int_{a}^{b} f(x) \,dx &=&\displaystyle \int_{g(a)}^{g(b)} f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \end{array}
\begin{array}{rllllll} \displaystyle \int f(x)g^{\prime}(x) \,dx &=&\displaystyle f(x)g(x) - \int f^{\prime}(x)g(x) \, dx \\ \\ \displaystyle \int_{a}^{b} f(x)g^{\prime}(x) \,dx &=&\displaystyle \Bigl[ f(x)g(x) \Bigr]_{a}^{b} - \int_{a}^{b} f^{\prime}(x)g(x) \, dx \end{array}
\begin{array}{llllll} \displaystyle\lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n}f\left( \frac{k}{n} \right) &=&\displaystyle \int_{0}^{1}f(x) \,dx \end{array}
暗記で良い人には関係ない話ですが。
目次
不定積分「積分で出てくる原始関数とか」
定積分「範囲が決まってる(両端が定数)積分」
定数倍の積分「関数を定数倍した時の積分」
和の積分「関数を足し算した時の積分」
置換積分「合成関数の微分から導かれるやり方」
部分積分「積の微分から導かれるやり方」
逆関数の積分「長方形から関数のやつを引いて求める」
区分求積法「 0 から 1 の範囲は定義で行ける」
不定積分 Indefinite Integral
|| 積分する時の原始関数の名前
閉区間 [a,b] 上で微分可能な F(x) のこと
\begin{array}{llllll} \displaystyle \frac{dF(x)}{dx}&=&f(x) \end{array}
\begin{array}{llllll} \displaystyle \int_{a}^{x}f(x) \,dx&=&\displaystyle F(x)-F(a) \end{array}
「微分の逆の操作」を指して
「不定積分」と呼ぶこともあります。
計算法則
微積分学の基本定理から
以下のような法則が導かれます。
\begin{array}{llllll} \displaystyle \frac{d}{dx}\int_{a}^{x} f(t) \, dt &=&\displaystyle f(x) \\ \\ \end{array}
「原始関数」の定義上これは当然
\begin{array}{llllll} \displaystyle \frac{dF(x)}{dx}&=&f(x) \end{array}
\begin{array}{rllllllll} \displaystyle \int_{a}^{x} f(t) \, dt &=&F(x)-F(a) \\ \\ \displaystyle \frac{d}{dx}\int_{a}^{x} f(t) \, dt &=&\displaystyle\frac{d}{dx}\Bigl( F(x)-F(a)\Bigr) \\ \\ &=&\displaystyle \displaystyle\frac{d}{dx} F(x) - \frac{d}{dx} F(a) \\ \\ &=&f(x) \end{array}
「定数の微分」が分かっていれば
特に疑問に思う部分は無いと思います。
積分定数
不定積分を考える場合
\begin{array}{rccllllll} \displaystyle \frac{d}{dx} ax^0 &=&\displaystyle 0 \\ \\ \displaystyle ax^0 &=&\displaystyle \int 0 \,dx \end{array}
定数の微分がこうなることから
\begin{array}{llllll} \displaystyle \int f(x) \, dx &=&F(x)+c_1 \\ \\ \displaystyle \int f(x) \, dx &=&F(x)+c_2 \\ \\ &&\vdots \end{array}
原始関数が無数に存在する
というのは直感的に明らか。
この定数は「定積分」であれば消えるので
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x) \,dx&=&\displaystyle \Bigl( F(b)+c\Bigr)-\Bigl( F(a)+c\Bigr) \\ \\ &=& F(b)-F(a) \end{array}
実際に気にすることはまあ無いんですけど
\begin{array}{llllll} \displaystyle \int f(x)\,dx &=& F(x) \end{array}
あくまで不定積分だとする場合
厳密には1つの関数には定まらないので
= の仕様上この式が正しいとは言えません。
\begin{array}{llllll} \displaystyle \int f(x) \, dx &=&F_1(x) \\ \\ \displaystyle \int f(x) \, dx &=&F_2(x) \end{array}
\begin{array}{llllll} \displaystyle F_1(x)&≠&F_2(x) \end{array}
なので厳密には無視するわけにはいかないため
\begin{array}{llllll} \displaystyle F_i(x)-F_j(x) &=&C \end{array}
違いが定数 C のみであることから
\begin{array}{llllll} \displaystyle \int f(x) \,dx&=&F(x)+C \end{array}
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle F_1(x)+C_1&=&F_2(x)+C_2 \end{array} \end{array}
「調整するための値」として
不定積分はこのように書く必要があります。
定積分 Definite Integral
|| 積分の範囲が定数で定まってる時の積分
不定積分の実践バージョンですね。
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x) \,dx&=&\displaystyle F(b)-F(a) \\ \\ &=&\displaystyle \Bigl[ F(x) \Bigr]_{a}^{b} \end{array}
具体的な値が求まるのはこっちで
この時の F(b)-F(a) を定積分と言います。
計算法則
定積分ならではの法則が存在します。
\begin{array}{llllll} \displaystyle \int_{a}^{a}f(x) \,dx &=& 0 \\ \\ \displaystyle \int_{\textcolor{pink}{a}}^{\textcolor{skyblue}{b}}f(x) \,dx &=& \displaystyle -\int_{\textcolor{skyblue}{b}}^{\textcolor{pink}{a}}f(x) \,dx \\ \\ \displaystyle \int_{a}^{b}f(x) \,dx &=& \displaystyle \int_{a}^{c}f(x) \,dx + \int_{c}^{b}f(x) \,dx \end{array}
3つ目がわりと重要です。
\begin{array}{llllll} \displaystyle \int_{a}^{a}f(x)\,dx &=&F(a)-F(a) \\ \\ \displaystyle \int_{b}^{a}f(x)\,dx &=&F(a)-F(b) \\ \\ \displaystyle \int_{a}^{b}f(x)\,dx &=&F(b)- \Bigl( F(c)-F(c) \Bigr) -F(a) \end{array}
証明はこんな感じ。
特に疑問に思う個所は無いと思います。
他にも
図形的な話になりますが
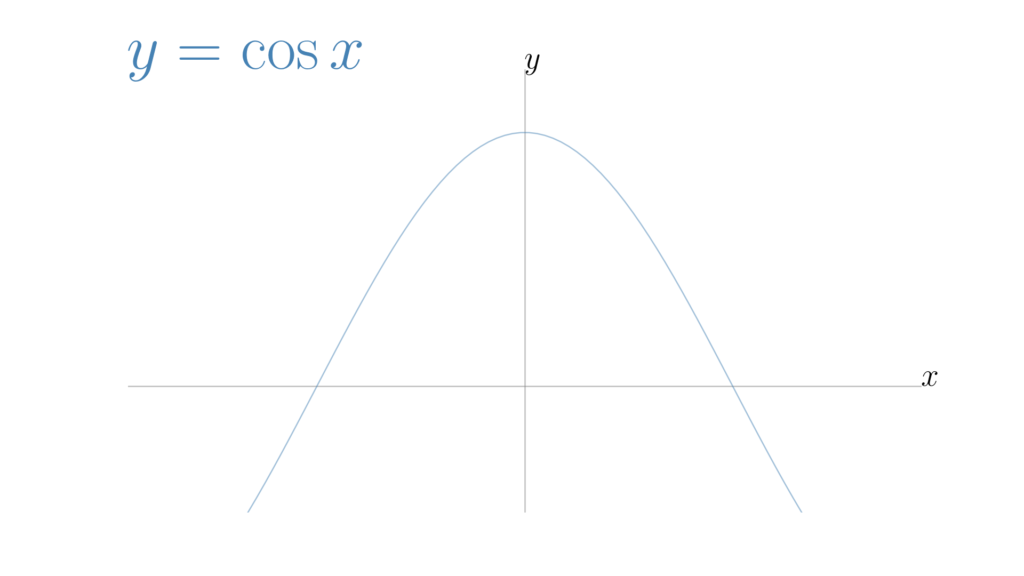
\begin{array}{llllll} \displaystyle \int_{-a}^{a}f(x) \,dx &=& \displaystyle 2\int_{0}^{a}f(x) \,dx \end{array}
y=x^2 や \cos x のような
偶関数( y 軸対称)ならこうなり
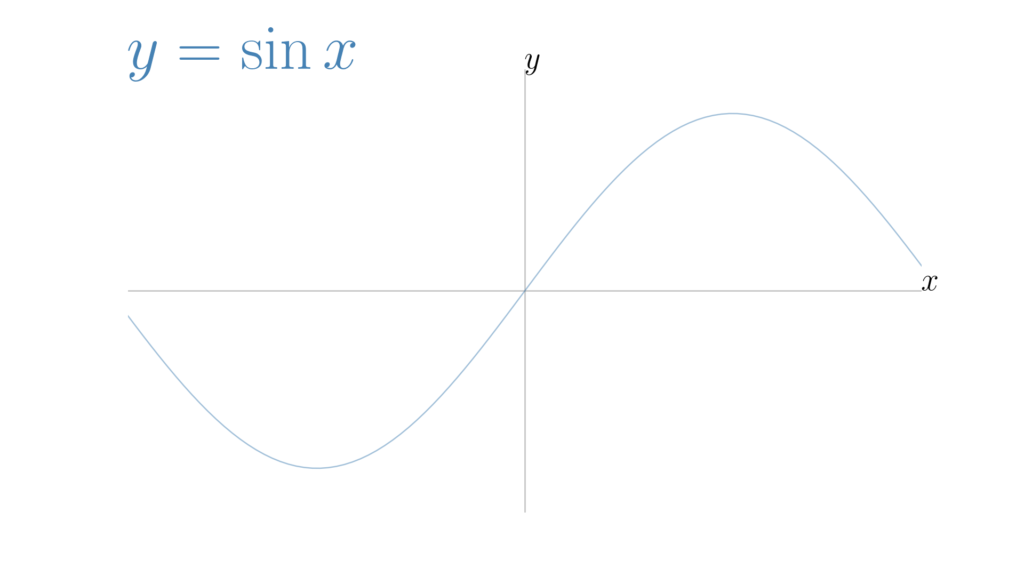
\begin{array}{llllll} \displaystyle \int_{-a}^{a}f(x) \,dx &=&0 \end{array}
y=x や \sin x のような
奇関数(原点対称)ならこうなります。
定数倍の積分
微分と同様
これは当たり前の結論に至ります。
\begin{array}{rlrlllll} \displaystyle \int cf(x) \, dx &=&\displaystyle c\int f(x) \, dx \\ \\ \displaystyle \int_{a}^{b} cf(x) \, dx &=&\displaystyle c\int_{a}^{b} f(x) \, dx \end{array}
証明はそのままです。
\begin{array}{llllll} \displaystyle \displaystyle \int_{a}^{b} cf(x) \, dx &=&cF(b)-cF(a) \\ \\ &=&\displaystyle c\Bigl(F(b)-F(a) \Bigr) \end{array}
頭の中ですぐ組み立てられると思います。
和の積分
これも微分と同様の結果に落ち着きます。
\begin{array}{rlclllll} \displaystyle \int \Bigl( f(x)+g(x) \Bigr) \,dx &=&\displaystyle \int f(x) \,dx +\int g(x) \,dx \\ \\ \displaystyle \int_{a}^{b} \Bigl( f(x)+g(x) \Bigr) \,dx &=&\displaystyle \int_{a}^{b} f(x) \,dx +\int_{a}^{b} g(x) \,dx \end{array}
証明も簡単
\begin{array}{llcllll} \displaystyle \Bigl(F(x)+G(x) \Bigr)^{\prime}&=&F^{\prime}(x)+G^{\prime}(x) \\ \\ &=&f(x)+g(x) \end{array}
\begin{array}{llllll} &&\displaystyle \int_{a}^{b} \Bigl( f(x)+g(x) \Bigr) \,dx \\ \\ &=& \displaystyle \Bigl( F(b)+G(b) \Bigr) - \Bigl( F(a)+G(a) \Bigr) \\ \\ &=&\displaystyle \Bigl(F(b)-F(a) \Bigr) +\Bigl( G(b)-G(a)\Bigr) \end{array}
「和の微分」を理解していれば
特に疑問の余地は無いと思います。
便利な形
対数関数の微分公式から
\begin{array}{crrllllll} \displaystyle \frac{f^{\prime}(x)}{f(x)} &=& \displaystyle \frac{d}{dx}\Bigl(\log |f(x)| +C \Bigr) \\ \\ \displaystyle \int\frac{f^{\prime}(x)}{f(x)} \,dx &=& \displaystyle \Bigl(\log |f(x)| +C \Bigr) \end{array}
このようなけっこう便利な形が導かれます。
置換積分 Substitution
「合成関数の微分」からすぐに導かれます。
\begin{array}{cccllll} t&=&g(x) \\ \\ \displaystyle g^{-1}(t)&=&x\end{array}
\begin{array}{rcrllllll} \displaystyle \int f(x) \,dx &=&\displaystyle \int f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \\ \\ \displaystyle \int_{a}^{b} f(x) \,dx &=&\displaystyle \int_{g(a)}^{g(b)} f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \\ \\ \\ \end{array}
\begin{array}{llllll} \displaystyle x&=&g(t) \end{array}
\begin{array}{ccrllllll} \displaystyle \displaystyle \int f(x) \,dx &=&\displaystyle \int f\Bigl( g(t) \Bigr) \frac{dx}{dt} \, dt \\ \\ \displaystyle \int_{a}^{b} f(x) \,dx &=&\displaystyle \int_{g^{-1}(a)}^{g^{-1}(b)} f\Bigl( g(t) \Bigr) \frac{dx}{dt} \, dt \end{array}
ただこれの説明は
「合成関数の微分」だけでは不十分です。
\begin{array}{cllllll} \displaystyle \left( f\Bigl( g(x) \Bigr) \right)^{\prime}&=&\displaystyle f^{\prime} \Bigl( g(x) \Bigr)g^{\prime}(x) \\ \\ \displaystyle \frac{df(x)}{dx}&=&\displaystyle \frac{f\Bigl( g(x) \Bigr)}{dg(x)}\frac{dg(x)}{dx} \end{array}
というのも
「変数」を変えてしまっている関係上
「積分をとる範囲」もまた変わっているので
\begin{array}{cccllll}\displaystyle t&=&g(x) \\ \\ \displaystyle x&=&g^{-1}(t) \\ \\ \\ g(a)&=&α \\ \\ g(b)&=&β \end{array}
積分範囲は
x から g(x) に変数を変更しても
答えに影響が出ないようにしなければなりません。
\begin{array}{llllll} \displaystyle g(a)&=&α \\ \\ \displaystyle g(b)&=&β \end{array}
\begin{array}{llllll} \displaystyle \int_{a}^{b} f(x) \,dx&=&\displaystyle \int_{α}^{β} f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \end{array}
ここまで
きちんと考慮するまでが置換積分になります。
\begin{array}{llllll} \displaystyle \displaystyle \int_{α}^{β} f\Bigl( g^{-1}(t) \Bigr) \frac{dx}{dt} \, dt \\ \\ \displaystyle \int_{α}^{β} f\Bigl( g^{-1}(t) \Bigr) \Bigl( g^{-1}(t)\Bigr)^{\prime} \, dt \end{array}
単純な微分の逆操作というより
これは式変形に近い考え方ですね。
役割
これは「式を簡単にする」とか
「積分できる形にする」とか
そういう場面で使われます。
\begin{array}{cllllll} \displaystyle f(x)&=&\displaystyle e^{2x+1} \end{array}
\begin{array}{rccllllll}t&=&2x+1\\ \\ \displaystyle x&=&\displaystyle\frac{t-1}{2} \\ \\ \displaystyle \frac{d}{dt}x&=&\displaystyle \frac{1}{2} \end{array}
\begin{array}{llllll} \displaystyle x&& 0&\to&1\\ \\t&& 1&\to&3\end{array}
\begin{array}{llllll}\displaystyle \int_{0}^{1} e^{2x+1} \,dx &=& \displaystyle \int_{1}^{3} e^t \frac{dx}{dt} \, dt \\ \\ &=& \displaystyle \int_{1}^{3} e^t \left( \frac{1}{2} \right) \, dt \\ \\ &=& \displaystyle \frac{1}{2}\int_{1}^{3} e^t \, dt \end{array}
具体的にはこういうのとか
\begin{array}{cllllll} \displaystyle f(x)&=&\displaystyle \frac{1}{x^2+1^2} \\ \\ x&=& \tan θ \end{array}
\begin{array}{llllll} \displaystyle x&&0&\to&1 \\ \\ θ&&0&\to&\displaystyle\frac{π}{4} \end{array}
\begin{array}{rccllllll} \displaystyle \frac{d}{dθ}x&=&\displaystyle \frac{1}{\cos^2 θ} \end{array}
\begin{array}{llllll}\displaystyle \int_{0}^{1} \displaystyle \frac{1}{x^2+1^2} \,dx &=& \displaystyle \int_{0}^{\frac{π}{4}} \frac{1}{\tan^2 θ +1} \frac{dx}{dθ} \, dθ \\ \\ &=& \displaystyle \int_{0}^{\frac{π}{4}} \frac{1}{\tan^2 θ +1} \left( \frac{1}{\cos^2 θ } \right) \, dθ \end{array}
\begin{array}{llllll} \displaystyle \tan^2 θ +1&=&\displaystyle\left( \frac{\sin θ}{\cos θ} \right)^2 +1 \\ \\ &=&\displaystyle \frac{\sin^2 θ}{\cos^2 θ} +1 \\ \\ \\ &=&\displaystyle \frac{\sin^2 θ}{\cos^2 θ} +\frac{\cos^2 θ}{\cos^2 θ} \\ \\ &=&\displaystyle \frac{\sin^2 θ+\cos^2 θ}{\cos^2 θ} \\ \\ \\ &=&\displaystyle \frac{1}{\cos^2 θ} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \int_{0}^{1} \displaystyle \frac{1}{x^2+1^2} \,dx &=&\displaystyle \int_{0}^{\frac{π}{4}} \frac{1}{\tan^2 θ +1} \left( \frac{1}{\cos^2 θ } \right) \, dθ \\ \\ &=&\displaystyle \int_{0}^{\frac{π}{4}} \frac{1}{\frac{1}{\cos^2 θ}} \left( \frac{1}{\cos^2 θ } \right) \, dθ \\ \\ &=&\displaystyle \int_{0}^{\frac{π}{4}} 1 \, dθ \end{array}
よくわかんないやつだと
こういうやつがあります。
部分積分 Integration by Parts
これは「積の微分」から求められます。
\begin{array}{llllll} \displaystyle \int f(x)g^{\prime}(x) \,dx &=&\displaystyle f(x)g(x) - \int f^{\prime}(x)g(x) \, dx \\ \\ \displaystyle \int_{a}^{b} f(x)g^{\prime}(x) \,dx &=&\displaystyle \Bigl[ f(x)g(x) \Bigr]_{a}^{b} - \int_{a}^{b} f^{\prime}(x)g(x) \, dx \end{array}
ただ、これはこのままだとただの式変形なので
\begin{array}{ccccccccccccllllll} \displaystyle \Bigl( f(x)g(x)\Bigr)^{\prime} &=&\displaystyle f^{\prime}(x)g(x) &+& f(x)g^{\prime}(x) \\ \\ \displaystyle f(x)g(x) &=&\displaystyle \int f^{\prime}(x)g(x) \,dx &+&\displaystyle \int f(x)g^{\prime}(x) \,dx \end{array}
どういう使い方をされるのかとか
その辺りがよく分からないと思います。
役割
「あまり変化しない関数」と
「微分すると次数が落ちる関数」のペア
\begin{array}{llllll} f(x)g(x)&=&\displaystyle x e^x \\ \\ \displaystyle f(x)g^{\prime}(x)&=&\displaystyle x e^x \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \int f(x)g^{\prime}(x) \,dx &=&\displaystyle f(x)g(x) - \int f^{\prime}(x)g(x) \, dx \end{array}
\begin{array}{llllll} \displaystyle \int x e^x \,dx &=&\displaystyle x e^x - \int (x)^{\prime}e^x \, dx \\ \\ &=&\displaystyle x e^x - \int e^x \, dx \\ \\ &=&\displaystyle x e^x - e^x \end{array}
\begin{array}{llllll} \displaystyle \int x e^x \,dx &=&\displaystyle e^x(x-1) +C\end{array}
あるいは
操作の過程で「元の式が現れる」場合とか
\begin{array}{llllll} \displaystyle f(x)g(x)&=&e^x\sin x \\ \\ \displaystyle f^{\prime}(x)g(x)&=&e^x\sin x \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \int f(x)g^{\prime}(x) \,dx &=&\displaystyle f(x)g(x) - \int f^{\prime}(x)g(x) \, dx \\ \\ \displaystyle \int f^{\prime}(x)g(x) \,dx &=&\displaystyle f(x)g(x) - \int f(x)g^{\prime}(x) \, dx \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \int f^{\prime}(x)g(x) \,dx &=&\displaystyle f(x)g(x) - \int f(x)g^{\prime}(x) \, dx \\ \\ \displaystyle \int e^x\sin x \,dx &=&\displaystyle e^x\sin x - \int e^x(\sin x)^{\prime} \, dx \\ \\ &=&\displaystyle e^x\sin x - \int e^x\cos x \, dx \end{array}
\begin{array}{llllll} \displaystyle \int e^x\cos x \,dx &=&\displaystyle e^x\cos x - \int e^x(\cos x)^{\prime} \, dx \\ \\ &=&\displaystyle e^x\cos x - \int e^x(-\sin x) \, dx \\ \\ &=&\displaystyle \displaystyle e^x\cos x + \textcolor{pink}{ \int e^x\sin x \, dx } \end{array}
\begin{array}{llllll} \displaystyle \int e^x\sin x \, dx&=&I \end{array}
\begin{array}{llllll} \displaystyle I &=&\displaystyle e^x\sin x - \int e^x\cos x \, dx \\ \\ &=& \displaystyle e^x\sin x - \left( e^x\cos x + \textcolor{pink}{ \int e^x\sin x \, dx } \right) \\ \\ \\ &=& \displaystyle e^x\sin x - \left( e^x\cos x + I \right) \\ \\ &=& \displaystyle e^x\sin x - e^x\cos x - I \end{array}
\begin{array}{rllllll} \displaystyle I &=&\displaystyle e^x\sin x - e^x\cos x - I \\ \\ 2I&=&\displaystyle e^x\sin x - e^x\cos x \\ \\ \\ 2I&=&\displaystyle e^x(\sin x - \cos x) \end{array}
\begin{array}{llllll} \displaystyle \int e^x\sin x \,dx &=&\displaystyle\frac{1}{2}e^x(\sin x - \cos x)+C \end{array}
なんかそういうのを微分する時に使われます。
\begin{array}{llllll} \displaystyle \int e^x f(x) \,dx \\ \\ \displaystyle \int x^n f(x) \,dx \end{array}
こんな感じだったらだいたいこれを使いますね。
逆関数の積分
よく分からない逆関数については
だいたい逆関数じゃない関数を使って求めます。
\begin{array}{cccllllll} y&=&f^{-1}(x) \\ \\ \displaystyle f(y)&=&x \end{array}
\begin{array}{llllll} \displaystyle \int f^{-1}(x) \,dx &=&\displaystyle yf(y)-\int f( y ) \,dy \end{array}
やってることは
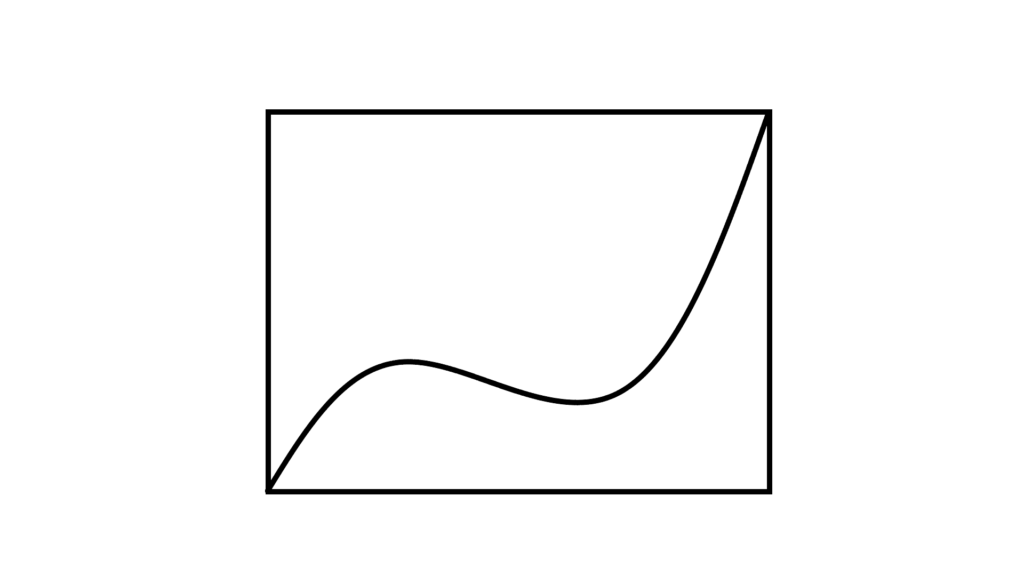
\begin{array}{cccl} yf(y)&-&\displaystyle\int f( y ) \,dy \\ \\ \displaystyle 長方形の面積 &-& f(x)の積分 \end{array}
まあこんな感じなので
特に疑問に思う部分は無いと思います。
ちなみにこれは
置換積分と部分積分でも導出できます。
\begin{array}{cllllll} \displaystyle \int f(x) \,dx&=&\displaystyle\int f(t)\frac{dx}{dt} \, dt \\ \\ \displaystyle \int f^{-1}(x) \,dx&=&\displaystyle\int f^{-1}(y)\frac{dx}{dy} \, dy \end{array}
\begin{array}{cccllllll} \displaystyle x&=&f(y) \\ \\ f^{-1}(x)&=&y \end{array}
ちょっと特殊ですが
\begin{array}{llllll} \displaystyle x&=&y \end{array}
ここで x を y で置換して入れ替えれば
\begin{array}{llllll} \displaystyle \displaystyle\int f^{-1}(y)\frac{dx}{dy} \, dy&=&\displaystyle\int y\frac{dx}{dy} \,dy \\ \\ &=&\displaystyle\int yf^{\prime}(y) \,dy \end{array}
こうなるので
後は部分積分すれば求められます。
\begin{array}{llllll} \displaystyle \displaystyle\int yf^{\prime}(y) \,dy&=&\displaystyle yf(y) - \int (y)^{\prime}f(y) \,dy \\ \\ &=&\displaystyle yf(y) - \int f(y) \,dy \end{array}
まあこれは検算ですね。
図形的に見る方が分かりやすいと思います。
役割
逆三角関数 \arcsin x とかの
逆関数の積分を計算する時に使えます。
\begin{array}{rcrcllllll} \displaystyle \arcsin x &=&y \\ \\ x&=& \sin y \end{array}
ここまでは置換とは関係ないただの事実
\begin{array}{llllll} \displaystyle x&=&y \end{array}
置換はこれで行う。
\begin{array}{llllll} \displaystyle \int \arcsin x \,dx &=&\displaystyle \int f^{-1}(x) \,dx \\ \\&=&\displaystyle yf(y) - \int f(y) \,dy \\ \\ \\ &=&\displaystyle y\sin y - \int \sin y \,dy \\ \\ &=&\displaystyle y\sin y - (-\cos y) \\ \\ \\ &=&\displaystyle y\sin y + \cos y \end{array}
\begin{array}{rlrlllll} \displaystyle \sin y &=&x \\ \\ y&=&\displaystyle \arcsin x \end{array}
\begin{array}{llllll} \displaystyle \cos y \\ \\ \cos^2 y &=& 1-\sin^2 y \\ \\ &=& 1-x^2 \end{array}
\begin{array}{llllll} \displaystyle \int \arcsin x \,dx &=&\displaystyle y\sin y + \cos y \\ \\ &=&\displaystyle x\arcsin x + \sqrt{1-x^2} \end{array}
入れ替わりまくって大変ですが
この操作のおかげでよく分からない積分が導けます。
区分求積法
これは「定積分」の話で
「積分の定義」からすぐに求められます。
\begin{array}{llllll} \displaystyle\lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n}f\left( \frac{k}{n} \right) &=&\displaystyle \int_{0}^{1}f(x) \,dx \end{array}
範囲が単純なので
「積分の定義」が分かるならすぐに分かるかと。
\begin{array}{llllll} \displaystyle 底辺 \times 高さ &=&\displaystyle\frac{1}{n} \times f\left( \frac{k}{n} \right) \end{array}
証明もこれが分かれば不要だと思います。
やってることは基本定理で出てきた話と同様なので。
ちなみに「置換積分」を使うと
範囲を無理矢理 0,1 にできます。
役割
だいたい「数列」の問題で使われます。
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n+h(k)} \\ \\ \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{h(n,k)} \end{array}
こんな感じの形だったら
だいたいこれを使いますね。
\begin{array}{ccccccll} \displaystyle n+h(k)&=&\displaystyle n\left(1+\frac{h(k)}{n} \right) \\ \\ \displaystyle \frac{1}{n+h(k)}&=&\displaystyle \frac{1}{n \left(1+\frac{h(k)}{n} \right)} \\ \\ &=&\displaystyle \frac{1}{n}\frac{1}{1+\frac{h(k)}{n}} \end{array}
\begin{array}{llllll} \displaystyle h(k)&=&ak \end{array}
\begin{array}{llllll} \displaystyle \frac{1}{n}\frac{1}{1+\frac{ak}{n}} &=& \displaystyle \frac{1}{n}\frac{1}{1+a\frac{k}{n}} \end{array}
\begin{array}{llllll} \displaystyle f\left( \frac{k}{n} \right) &=&\displaystyle \frac{1}{1+a\frac{k}{n}} \\ \\ \displaystyle f\left( x \right) &=&\displaystyle \frac{1}{1+ax} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n+ak} &=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n}\frac{1}{1+a\frac{k}{n}} \\ \\ &=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n} \frac{1}{n}f\left( \frac{k}{n} \right) \\ \\ &=&\displaystyle \int_{0}^{1} f(x)\,dx \\ \\ &=&\displaystyle \int_0^{1}\frac{1}{1+ax} \,dx \end{array}
例えばこんな具合に。
