|| リーマン積分より広い範囲をカバーしてる積分
「だいたいなんでも積分できる」積分のこと
スポンサーリンク
目次
リーマン積分「基本的な積分のやり方」
定義関数「関数を分解できることがある」
ディリクレ関数「リーマン積分不可の代表例」
可測関数「変な結果にならない普通の関数」
単関数「定義関数で作れる直線を集めた関数」
近似定理「単関数が f(x) に近似する感じ」
ルベーグ積分「区間 → 任意の集合」
ルベーグ積分可能「可測集合ならいける」
これについて
深くはこの記事単体では書ききれていません。
この辺りの知識については
長くなるので別の記事にまとめています。
リーマン積分 Riemann Integral
|| 細い長方形で全体を定義する方法
みんなが知ってる積分のこと
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x)&=&F(b)-F(a) \end{array}
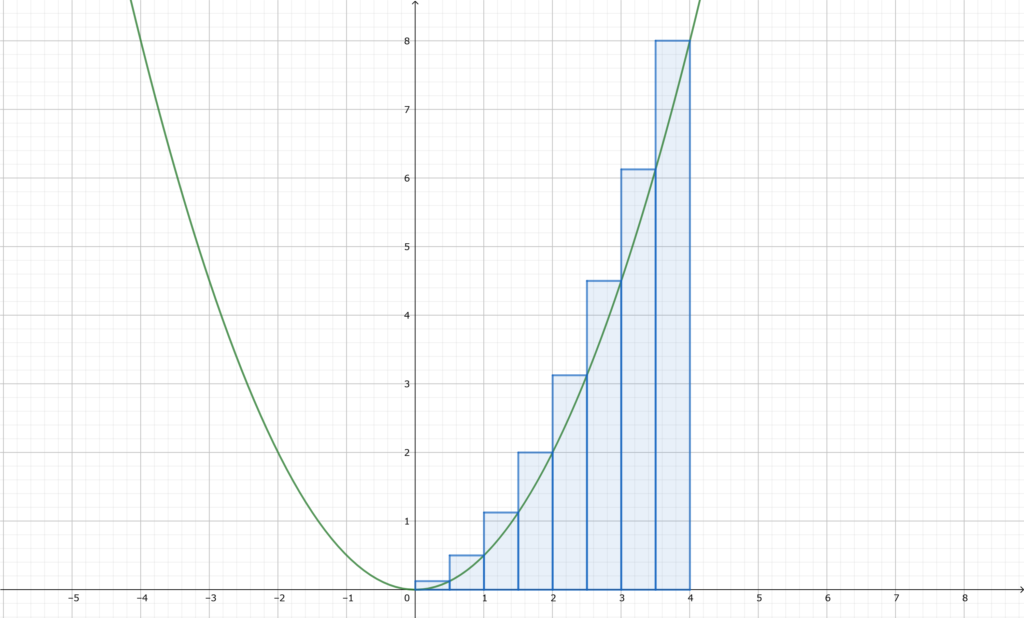
厳密には「リーマン和」ってやつで定義されてます。
リーマン和
これはちょっと複雑ですが
要は ↑ の図形を説明したもので
\begin{array}{llllll} \displaystyle a&=&x_0&<&x_1&<&x_2&<&\cdots&<&x_n&=&b \end{array}
区間 [a,b] の有限分割から
\begin{array}{llllll} c_k&∈& \displaystyle [x_{k-1},x_{k}] \end{array}

\begin{array}{llllll} \displaystyle 縦\times 横 &=&f(c_k)\times (x_{k}-x_{k-1}) \end{array}
\begin{array}{llllll} \displaystyle S_{\mathrm{riemann}}&=&\displaystyle \sum_{k=1}^{n}f(c_k)(x_{k}-x_{k-1}) \end{array}
『細長い長方形』の「面積の総和」として
これは普通に導かれます。
リーマン積分可能
以上を踏まえて
「積分可能」という概念は
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x)&=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}f(c_k)(x_{k}-x_{k-1}) \end{array}
基本的にはこのような形で定義されています。
補足しておくと
細かい話ですが
「区間 [x_{k-1},x_{k}] の幅」については
\begin{array}{llllll} \displaystyle Δ&=&\displaystyle\max(x_k-x_{k-1}) \end{array}
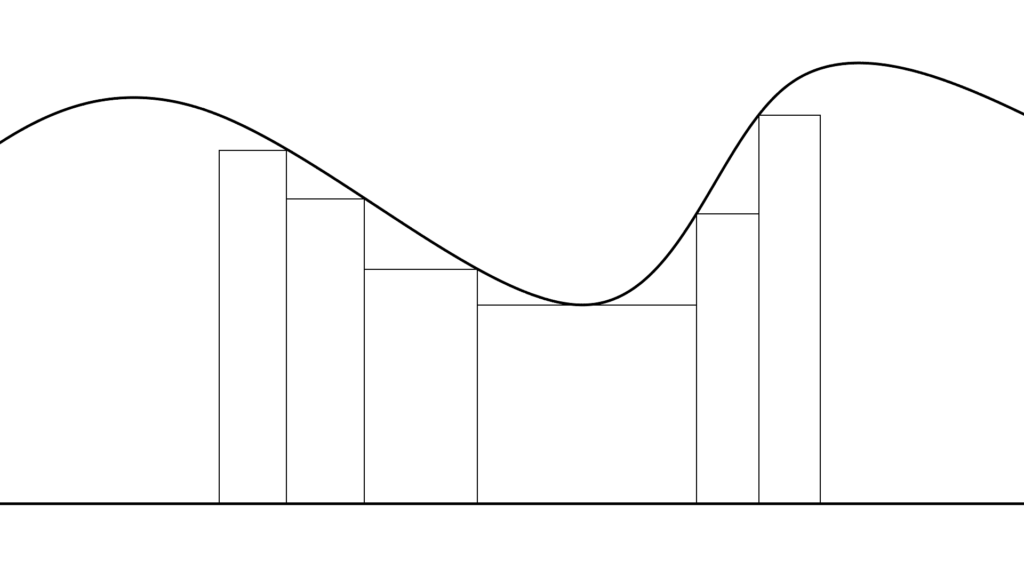
このような形で定義されていて
\begin{array}{cccllllll} \displaystyle n&\to&\infty \\ \\ Δ&\to&0 \end{array}
この関係が成り立つと定義されています。
(分割の幅を固定すると近似できない)
リーマン積分可能の別表現
↑ の話と似たような話ですが
「リーマン積分可能」には
\begin{array}{rllllll} \displaystyle \displaystyle \inf\Bigl( \{ f(x) \mid x∈[x_{k-1},x_k] \} \Bigr)&=&f(m_k) \\ \\ \displaystyle \sup\Bigl( \{ f(x) \mid x∈[x_{k-1},x_k] \} \Bigr) &=&f(M_k) \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}f(m_k)(x_{k}-x_{k-1}) &=&S_{\mathrm{inf}} \\ \\ \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}f(M_k)(x_{k}-x_{k-1})&=&S_{\mathrm{sup}} \end{array}
\begin{array}{llllll} S_{\mathrm{inf}} &=&\displaystyle \int_{a}^{b}f(x)&=&S_{\mathrm{sup}} \end{array}
このような「連続」と似た表現もあります。
わりと見る考え方なので一応紹介。
(外測度と内測度みたいな話)
定義関数 Indicator Function
|| リーマン積分不可の関数を作れるやり方
かなり実用性のある関数で
\begin{array}{rcl} \displaystyle 1_D(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∉D \end{array} \right. \\ \\ \\ \displaystyle χ_P(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&P(x)\,\,\mathrm{is} \,\, \mathrm{True} \\ \\ 0 &&P(x) \,\,\mathrm{is} \,\, \mathrm{False} \end{array} \right. \end{array}
条件を狭める時とかでよく使います。
(よく使うのに積分し辛い代表例)
ディリクレ関数 Dirichlet Function
|| リーマン積分できない代表的な定義関数
リーマン積分不可でルベーグ積分可能と言ったら
\begin{array}{llllll} \displaystyle \displaystyle 1_Q(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈Q \\ \\ 0 &&x∈R\setminus Q \end{array} \right. \end{array}
だいたいこれが引き合いに出されます。
リーマン積分不可
区間 [x_{k-1},x_{k}] における
関数 f(x) の上限と下限は
\begin{array}{llllll} \sqrt{2},2&∈& \displaystyle \left[ 0,2 \right] \\ \\ \sqrt{2},2&∈& \displaystyle \left[ \sqrt{2},\sqrt{5} \right] \\ \\ \sqrt{2},2&∈& \displaystyle \left[ \sqrt{2},2 \right] \end{array}
端点を含め「区間」が 2 点以上を含むことから
\begin{array}{rllllll} \displaystyle \displaystyle \inf\Bigl( \{ 1_Q(x) \mid x∈[x_{k-1},x_k] \} \Bigr)&=&1_Q(m_k) \\ \\ &=&0 \\ \\ \\ \displaystyle \sup\Bigl( \{ 1_Q(x) \mid x∈[x_{k-1},x_k] \} \Bigr) &=&1_Q(M_k) \\ \\ &=&1 \end{array}
無理数と有理数の両方を含むため
必ずこのようになります。
\begin{array}{llllll} \displaystyle 0&=&x_0&<&x_1&<&x_2&<&\cdots&<&x_n&=&1 \end{array}
またディリクレ関数の積分区間をこうすると
\begin{array}{llllll} \displaystyle \sum_{k=1}^{n}(x_{k}-x_{k-1})&=&(\textcolor{gray}{x_1}-x_0)+(\textcolor{gray}{x_2}-\textcolor{gray}{x_1})+\cdots+(x_n-\textcolor{gray}{x_{n-1}}) \\ \\ &=&-x_0+x_n \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}(x_{k}-x_{k-1})&=&1-0 \end{array}
この値は当然こう
\begin{array}{llllll} \displaystyle S_{\mathrm{inf}}&=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}0(x_{k}-x_{k-1}) \\ \\ &=&0 \\ \\ \\ S_{\mathrm{sup}}&=& \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}1(x_{k}-x_{k-1}) \\ \\ &=&1 \end{array}
ということは
つまりリーマン和の下限と上限はこうなるので
\begin{array}{llllll} \displaystyle S_{\mathrm{inf}}&=&0&≠&1&=&S_{\mathrm{sup}} \end{array}
結果、一致しないことから
これはリーマン積分不可となります。
可測関数 Measurable Function
|| ほとんどの関数のこと
「ルベーグ可測」な関数のことで
\begin{array}{llllll} \displaystyle (X,σ_X)&→&(Y,σ_Y) \end{array}
\begin{array}{llllll} \displaystyle f&:&X&\to&Y \\ \\ f^{-1}&:&X&←&Y \end{array}
\begin{array}{cclllllll} \displaystyle D&∈&σ_Y &&\to&& f^{-1}(D)&∈&σ_X \end{array}
ほぼ全ての関数はこれに含まれます。
含まれないやつはかなり特殊です。
(とりあえず普通の関数だと思ってOK)
具体的には
単関数 Simple Function
|| 定義関数の性質から導かれるやつ
関数を足し算の集まりに変換するやつ
\begin{array}{llllll} \displaystyle φ(x)&=&\displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \end{array}
以下の性質から導かれます。
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle φ(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
\begin{array}{cllllll} \displaystyle a_1 1_{D_1}(x) \\ \\ a_2 1_{D_2}(x) \\ \\ \vdots \\ \\ a_n 1_{D_n}(x) \end{array}
\begin{array}{llllll} \displaystyle μ \left( \displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \right)&=&\displaystyle μ\Bigl( a_1 1_{D_1}(x)\Bigr) +\cdots + μ\Bigl( a_n 1_{D_n}(x)\Bigr) \end{array}
記号がややこしいですが
よく見ると当たり前の話ですね。
\begin{array}{cccllllll} \displaystyle \int_{-\infty}^{\infty}1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} \,dx \\ \\ \displaystyle \int_{-\infty}^{\infty}f(x)1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} f(x) \,dx \end{array}
ちなみに定義関数はこういう性質も持ってます。
単関数の積分
「リーマン積分」及び「ルベーグ積分」
これはその雛型とも言えるもので
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle φ(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
この前提の基
\begin{array}{llllll} \displaystyle D &=&\displaystyle \bigcup_{k=1}^{n}D_k \\ \\ &=&\displaystyle D_1∪D_2∪ \cdots ∪D_n \end{array}

\begin{array}{llllll} \displaystyle \int_{D} φ(x) \, μ(dx) &=&\displaystyle\sum_{k=1}^{n}a_k \, μ(D_k) \end{array}
\begin{array}{llllll} \displaystyle μ(dx)&=&μ(D_k) \\ \\ μ(dx)&=&μ([x_{k-1},x_k]) \\ \\ &=&x_k-x_{k-1} \end{array}
「単関数の積分」は
このように定義されていて
\begin{array}{llllll} \displaystyle \int_{D}f(x) \,dx \end{array}
これが『積分値の近似』で使われる
「内測度」「外測度」の具体的な中身になります。
単関数近似定理 Simple Approximation
|| 多項式で近似できる感じ
テイラーの定理的な話で
\begin{array}{cccccl} \\ \\ 0&≤&φ_n(x)&≤&f(x) \\ \\ \\ &&φ_n(x)&\to&f(x) \end{array}
これにより
「単関数」での近似に正当性が与えられています。
ただし可測関数全体は
微分できない関数(定義関数など)があるので
テイラーの定理ではカバーできません。
ちょっと厳密な話
直感的な話としては
f(x) は「非負値可測関数」
φ_n(x) は「 n が増えると単調増加」する「単関数」
このように定めると
「リーマン積分」的な感覚で
この定理の主張は理解することができます。

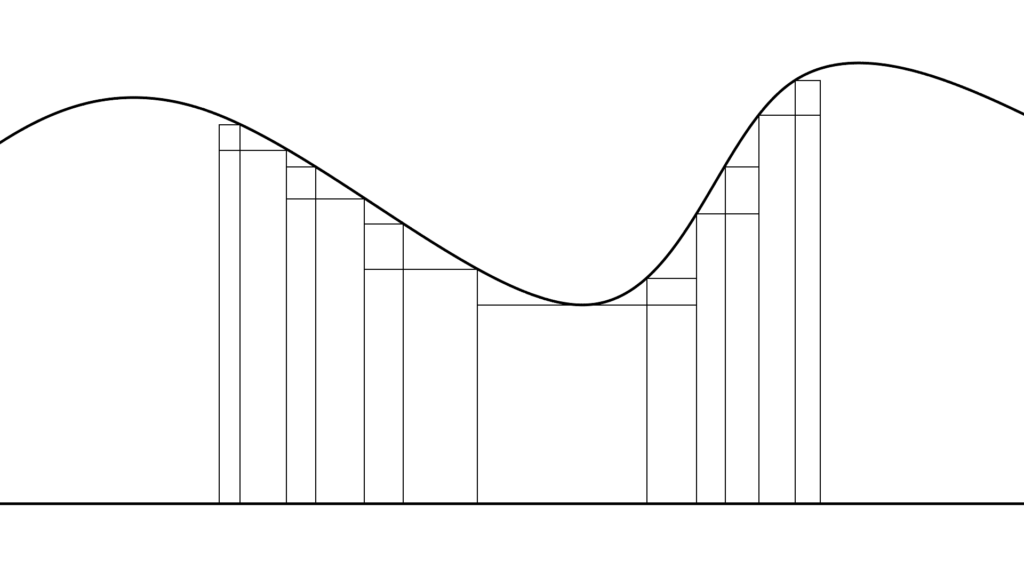
ちなみに「単調増加する単関数」ってのは
こんな感じです。
\begin{array}{llllll} \displaystyle φ_n(x)&≤&f(x) \end{array}
この前提のもと
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} φ_n(x)&=&\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}a_k 1_{D_k}(x) \end{array}
このようにすると
「単調増加する」ことから
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}a_k 1_{D_k}(x)&=&f(x) \end{array}
これが f(x) に近似するというのは
直感的に分かると思います。
単関数近似定理の証明については
単関数 f_n の構成がメインになって
本題から逸れるので別の記事で解説します。
ルベーグ積分 Lebesgue Integral
|| 単関数と近似定理から導かれる関係
だいたい「単関数」によって定義されてます。
\begin{array}{llllll} \displaystyle 0&≤&φ(x)&≤&f(x) \end{array}
\begin{array}{llllll} \displaystyle i≠j&&\to&&D_i∩D_j=∅ \end{array}
\begin{array}{llllll} \displaystyle D&=&D_1∪D_2∪\cdots∪D_n \end{array}
\begin{array}{llllll} \displaystyle \int_{D}f(x) \,μ(dx) &=&\displaystyle \sup \int_{D}φ(x) \, μ(dx) \\ \\ &=&\displaystyle \sup \sum_{k=1}^{n}a_k \, μ(D_k) \end{array}
これを「ルベーグ積分」と言い
これにより定義関数の積分が明確化されました。
ルベーグ可積分 Integrable
|| ルベーグ積分できるとは
定義された「ルベーグ積分できる」を意味する用語
\begin{array}{llllll} \displaystyle \int_{D} \Bigl| f(x) \Bigr| \,μ(dx)&<&\infty \end{array}
『可測関数 f(x) 』を
『ルベーグ積分すると有限の値になる』
こういう形でこの用語は定義されています。
\begin{array}{llllll} \displaystyle \infty-\infty &&× \end{array}
意味合いとしてはそのまま
「 f(x) が無限になる点」など
そういったものが無いことをこれは意味しています。
ディリクレ関数はルベーグ積分可能
「リーマン積分」できなかった関数でも
「ルベーグ積分」ならできる
\begin{array}{llllll} \displaystyle \int_{[0,1]}1_Q(x) \,dμ(x) &=&\displaystyle \sup \int_{[0,1]}φ(x) \, dμ(x) \\ \\ &=&\displaystyle \sup \sum_{k=1}^{n}1_Q(x_k) \, μ(D_k) \\ \\ \\ &=&\displaystyle \sup \Bigl( 1\times μ(Q_{[0,1]})+ 0\times μ([0,1]\setminus Q_{[0,1]}) \Bigr) \\ \\ &=&\displaystyle \sup \Bigl( 1\times 0+ 0\times 1 \Bigr) \\ \\ &=&0 \end{array}
その代表例として
ディリクレ関数の積分は
このような結果に落ち着きます。
補足しておくと
\begin{array}{llllll} \displaystyle μ \Bigl( \{q_0\}∪\{q_1\}∪\cdots \Bigr)&=&\displaystyle μ \Bigl( \{q_0\} \Bigr) +μ \Bigl( \{q_1\} \Bigr)+\cdots \\ \\ &=&0+0+0+\cdots \\ \\ &=&0 \end{array}
「有理数の測度」と
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle A⊂B \\ \\ μ(A)<\infty \end{array} \right) &\to& \displaystyle \left( \begin{array}{llllll} \displaystyle μ(A)≤μ(B) \\ \\ μ(B\setminus A)=μ(B)-μ(A) \end{array} \right) \end{array}
「差集合の測度」がこうなるので
\begin{array}{llllll} \displaystyle μ\Bigl([0,1]∩Q \Bigr)&=&0 \\ \\ \\ μ \Bigl( [0,1]∩R\setminus Q\Bigr)&=&μ\Bigl( [0,1] \setminus Q \Bigr) \\ \\ &=&\displaystyle μ\Bigl([0,1] \Bigr)-μ(Q) \\ \\ &=&μ\Bigl([0,1] \Bigr) \end{array}
「有理数」と「無理数」の測度はこうなる

そしてこの事実から
「有理数のみの領域」と
「無理数のみの領域」が考えられて
\begin{array}{llllll} D_1&& \displaystyle 1\times μ([0,1]∩Q) \\ \\ D_2 && 0\times μ([0,1]\setminus Q) \end{array}
結果、区間 [0,1] 全体が 2 分割され
この「測度」から積分値が求まります。
リーマン積分との違い
リーマン積分では
\begin{array}{llllll} \displaystyle x&∈&[x_{k-1},x_k] \end{array}
「区間の分割」という形で
図形を近似していくわけですが
\begin{array}{lcrllll} \displaystyle D_1&&Q \\ \\ D_2 &&R\setminus Q \end{array}
ルベーグ積分では
「区間の分割」に限らず
「領域の定義」によって全体を分割できるため
\begin{array}{rcl} \displaystyle 1_D(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∉D \end{array} \right. \end{array}
定義関数で不連続な関数を作っても
「区間の分割」にこだわることなく
\begin{array}{llllll} \displaystyle 1\times μ(D) +0\times μ(D^c)\end{array}
「集合の測度」から
直接的に積分値を算出できます。
