ボレル集合 Borel set

|| 実数の集合についてのあれこれ

「実数」の「完全加法族」のこと

スポンサーリンク

　

　

　

---

事前知識

　

測度空間「ボレル集合を考える理由」

完全加法族「矛盾なく足し算ができるやつ」

　

極限「実数が持つ近付けるっていう感覚の形式表現」

区間「実数を集合で表現する代表的な方法の１つ」

開集合「実数で定義される区間を厳密に定義するやつ」

位相空間「連続を矛盾なく定義できる枠組み」

　

　

　

　

　

目次

　

ボレル集合「実数バージョンの完全加法族」

　

　　　定義のちょっとした解説

　　　定義に問題が無いかの確認

　

　

　

　

　

---

　

「位相空間」「完全加法族」上で定義されるので

「開集合」とか「極限」を理解してないと

こいつについて厳密には理解できないと思います。

　

　

ただ、これ自体はそんな難しいものではないので

感覚的にはなんとなく分かるかと。

　

　

　

　

　

---

ボレル集合 Borel Set

　

|| 実数の測度を考える時に出てくるやつ

「実数」上で「普通の操作ができる集合」のこと

（いろんなものが含まれるように調整されてる）

　

$\begin{array}{llllll} \displaystyle (-\infty,\infty)&→&(0,1),(-1,2),\cdots \\ \\ &→&\{0\},N,Q,(0,1),[0,2),\cdots \end{array}$

　

$\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \\ \\ O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \\ \\ σ\Bigl( O(X)\Bigr) &\mathrm{is} & σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}$

　

矛盾が出ないよう

そのまま「完全加法族」として定義されています。

　

$\begin{array}{llllll} \displaystyle \mathrm{Borel}(X)&=&σ\Bigl( O(X)\Bigr) \end{array}$

　

この $\mathrm{Borel}(X)$ が「ボレル集合族」で

この「ボレル集合族の要素」が「ボレル集合」になります。

（具体的には区間とか点集合とかのこと）

　

　

　

　

　

ボレル集合族の中身

　

この時点じゃなんで？って話かもしれませんが

　

$\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}$

　

こいつは「開集合」と「閉集合」の両方と

「任意の区間」「点の集まり」を中身に持ちます。

　

　

　

　

　

ボレル集合の役割

　

これの役割を簡単に言うなら

「区間」を「矛盾なく使うためのもの」って感じで

　

$\begin{array}{cclcccll} \displaystyle (a,b)&=&\{ x∈R \mid a<x<b \} \\ \\ [a,b]&=&\{ x∈R \mid a≤x≤b \} \\ \\ (a,b]&=&\{ x∈R \mid a<x≤b \} \\ \\ [a,b)&=&\{ x∈R \mid a≤x<b \} \end{array}$

　

「ボレル集合族（ボレル集合の集まり）」は

そのために整備された「集合の集まり」になります。

　

　

なので順番は

「区間・点・それらの組み合わせ」が先

　

$\begin{array}{llllll} \displaystyle \begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array} &→&\mathrm{Borel}(X) \end{array}$

　

「ボレル集合族 $\mathrm{Borel}(X)$ 」の定義は

これを含むように調整されています。

　

　

　

　

　

位相空間が保証すること

　

問題なく「極限」の操作ができる

「開集合 → 開集合」「閉集合 → 閉集合」になる

そういったことを保証するのが「位相空間」の役割で

　

$\begin{array}{llllll} \displaystyle (X,O) \end{array}$

　

$\begin{array}{llllll} \displaystyle \lim_{ε\to0} ε &=&0 \end{array}$

　

　

具体的には

「集合の操作」を制限することで

　

$\begin{array}{cccccccccll} \displaystyle && A&⊂&S&⊂&B \\ \\ ∅&⊂& A&⊂&S&⊂&B&⊂&X \end{array}$

　

必ず「大きい値と小さい値が分かる」

つまり「より大きい・小さい値が存在する」

　

$\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}&&〇 \\ \\ \displaystyle \bigcap_{n=1}^{\infty}&&× \\ \\ \displaystyle \bigcup_{n=1}^{k}&&〇 \end{array}$

　

「この操作はしていい」

「この操作では矛盾が出る」

みたいなことをこれは保証しています。

　

　

　

　

　

開集合とは

　

「区間」「位相空間」を定義する上で

その存在を必ず考えなければならないもの

　

$\begin{array}{llllll} \displaystyle 1&<&a&<&2 \end{array}$

　

それが「開集合」という概念で

　

$\begin{array}{llllll} \displaystyle \mathrm{Ball}(α,ε)&=&\{ x∈X \mid |x-α|<ε \} \\ \\ &=&(α-ε,α+ε) \end{array}$

　

　

「点の実態（見える大きさのある点）」

という図形の直感的な性質とか

　

$\begin{array}{llllll} \displaystyle (0,3)&=&\{ x \mid 0<x<3 \} \end{array}$

　

この集合の境界はどうなってんの？とか

そういうのを厳密に定義する時に使われます。

　

　

それと変な感じがしますが

　

$\begin{array}{llllll} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \end{array}$

　

これは「開集合の補集合」である

「閉集合」とセットの概念になります。

（片方だけではカバー範囲が狭い上に使いにくい）

　

　

　

　

　

開集合のややこしい定義

　

「 $X$ の開集合 $O$ 」という概念は

　

$\begin{array}{llllll} \displaystyle && &&O&⊂&X \\ \\ && \mathrm{Ball}(α,ε)&⊂&O \\ \\ α&∈&\mathrm{Ball}(α,ε) \end{array}$

　

$O$ の中の任意の点 $α∈\mathrm{Ball}(α,ε)$

これを持つ集合 $\mathrm{Ball}(α,ε)$ が常に内側にある

　

　

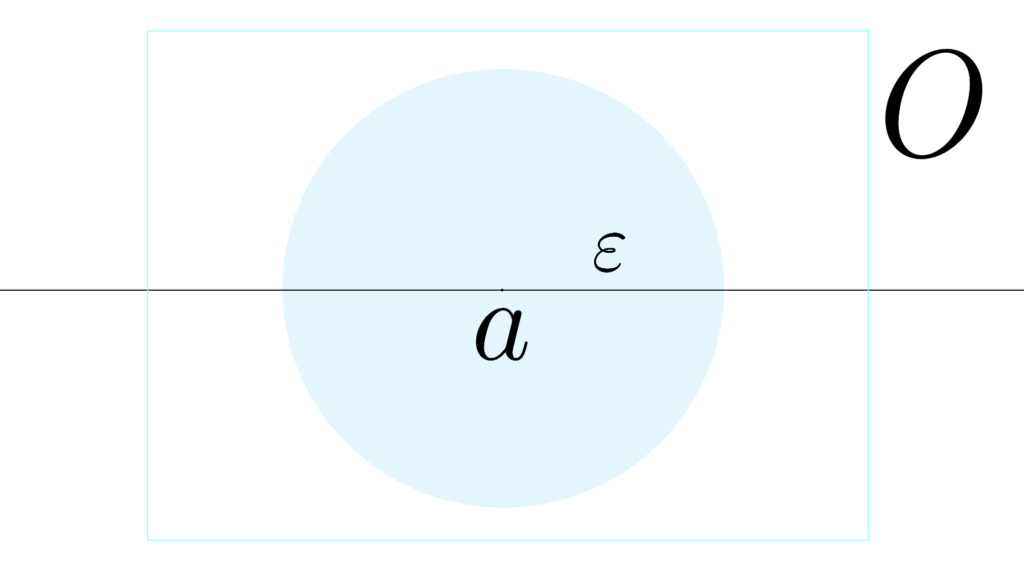
$\begin{array}{llllll} \displaystyle \mathrm{Ball}(α,ε)&⊂&O \end{array}$

　

これが「 $O$ の全ての点 $α$ で成り立つ」

　

　

そういう集合 $O$ のことを指していて

　

　

主に「境界を含まないとは」とか

「ある点 $α$ のすっごい近くにある」とか

そういう感じのことを厳密に説明するとき使われます。

　

　

　

　

　

完全加法族が保証すること

　

いろんな操作が問題なくできる

ということをこれは保証しています。

　

$\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ S∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A,B∈σ&\to&\displaystyle A\setminus B∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n ∈σ \end{array} \right) \end{array}$

　

具体的には

こういった「集合の基本操作」が

「矛盾を導かない」ということが保証できます。

　

　

今回の場合

　

$\begin{array}{llllll} \displaystyle (0,2)∪(1,3)&=&(0,3) \\ \\ (0,2)∩(1,3)&=&(1,2) \end{array}$

　

「区間」という「集合」について

問題なくこういった操作を行える

　

$\begin{array}{ccc} [a,b)&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}$

　

あるいはこういったものも含まれる

というようなことを保証するのに

この考え方が使われる感じです。

　

　

　

　

　

---

ボレル集合の定義の解説

　

「位相空間 $(X,O)$ 」上であること

　

$\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \end{array}$

　

「 $X$ から生成された開集合全体 $O(X)$ 」

　

$\begin{array}{cccl} O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \end{array}$

　

「 $O(X)$ から生成された完全加法族 $σ\Bigl( O(X)\Bigr)$ 」

　

$\begin{array}{cccl} σ\Bigl( O(X)\Bigr) &\mathrm{is} & σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}$

　

これらを一つずつ解説していくと

　

　

　

　

　

位相空間だと

　

まず「位相空間」についてですが

（長くなるので詳細は省きます）

　

$\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \end{array}$

　

$\begin{array}{llllll} \displaystyle O&⊂&2^X \end{array}$

　

これは特定の「操作」によって

『ある操作が可能であるか』に『変化が無い』

つまり「構造の変化が起きない」ことを保証していて

　

　

具体的には

以下のような操作を行った時

　

$\begin{array}{rcccc} \displaystyle A∩B∈τ&&〇 \\ \\ \displaystyle\bigcap_{i∈I}A_i∈τ&&× \\ \\ \\ A∪B∈τ&&〇 \\ \\ \displaystyle\bigcup_{i∈I}A_i∈τ&&〇 \end{array}$

　

必ず「開集合 → 開集合」になる操作があって

その操作のみを許可する感じです。

（許可された操作で作ったものだけで構成）

　

　

　

　

　

ある集合 $X$ から作られた開集合

　

「 $X$ から生成された開集合全体 $O(X)$ 」について

　

$\begin{array}{cccl} O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \end{array}$

　

これは大雑把にしか記述できませんが

　

$\begin{array}{llllll} \displaystyle X&⊂&R=(-\infty,\infty) \end{array}$

↓

$\begin{array}{ccc} \displaystyle (0,1)&⊂&X \\ \\ (1,3)&⊂&X \\ \\ (a,b)&⊂&X \\ \\ &\vdots& \end{array}$

　

要はこういう感じの話で

「全体 $X$ から」作ることができる

「開集合だけ」で構成されていることを意味します。

　

　

　

最終工程である「完全加法族」

これが「補集合」を中身に含むので

　

$\begin{array}{llllll} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \end{array}$

　

「閉集合全体」もまた

最終的には「ボレル集合族」の中に含まれます。

　

　

　

　

　

開集合 $O(X)$ から作られる完全加法族

　

これも考え方は似たようなもので

　

$\begin{array}{cc} σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}$

　

$O(X)$ の要素のみに

　

$\begin{array}{rcr} \displaystyle O(X)&⊂&σ\Bigl( O(X)\Bigr) \\ \\ A∈O(X)&→&A∈σ\Bigl( O(X)\Bigr) \end{array}$

　

「完全加法族」の定義に則って

↓ の操作を加えると

　

$\begin{array}{rcr} \displaystyle A∈O(X)&→&A^c∈σ\Bigl( O(X)\Bigr) \\ \\ A_1,A_2,...,A_n,...∈O(X)&→&\displaystyle \bigcup_{n=1}^{\infty}A_n∈σ\Bigl( O(X)\Bigr) \end{array}$

　

この $σ\Bigl( O(X)\Bigr)$ が出来上がります。

　

　

　

補足しておくと

この過程で「補集合」を含めることになるので

　

$\begin{array}{ccc} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \\ \\ (\mathrm{Closed\,\,Set})^c&=&\mathrm{Open\,\,Set} \end{array}$

　

「開集合の補集合」は「閉集合」であり

「閉集合の補集合」は「開集合」であることから

　

$\begin{array}{ccc} \displaystyle \mathrm{Open\,\,Set}&∈&σ\Bigl( O(X)\Bigr) \\ \\ \mathrm{Closed\,\,Set}&∈&σ\Bigl( O(X)\Bigr) \end{array}$

　

「位相空間」を「開集合族」で定義しても

その「補集合」である「閉集合族」で定義しても

これの中身は同じになります。

　

　

　

　

　

ボレル集合と区間

　

以上の「ボレル集合族の定義」は

『良い感じに調整された定義』です。

　

$\begin{array}{llllll} \displaystyle \mathrm{Borel}(X)&=&σ\Bigl( O(X)\Bigr) \end{array}$

　

なので問題を含んでいる可能性があります。

（結論の先取りですが問題はありません）

　

　

とまあそういうわけですから

念のため「ボレル集合」の定義に問題が無いか

　

$\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}$

　

ここできちんと確認しておきます。

　

　

　

　

　

開集合と閉集合

　

確認する上で必要になる以下に関して

　

$\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Open\,\,Sets} \\ \\ [a,b]&∈&\mathrm{Closed\,\,Sets} \\ \\ \\ \{a\}&∈&\mathrm{Closed\,\,Sets} \\ \\ N&∈&\mathrm{Closed\,\,Sets} \end{array}$

　

ちゃんとやりたいんですが

厳密な話をするとなると

「開集合」を深堀する必要があるので

　

$\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}$

　

とりあえずこの記事では

これらについては特に言及しません。

　

　

というわけで

以上のことはひとまず飲み込んで

「ボレル集合」について確認すると

　

$\begin{array}{llllll} \displaystyle \mathrm{Open\,\,Set}&∈& \mathrm{Borel}(X) \\ \\ \mathrm{Closed\,\,Set}&∈& \mathrm{Borel}(X) \end{array}$

　

「開集合」「閉集合」は

間違いなく「ボレル集合」であることから

　

$\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \end{array}$

　

ひとまず

これらは「ボレル集合」であると言えます。

　

　

　

　

　

開集合でも閉集合でもないもの

　

問題となるのは以下のような

「開集合」「閉集合」ではないもので

　

$\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}$

　

これらが「ボレル集合」であるかどうかは

この時点ではまだ分かっていません。

　

$\begin{array}{ccc} \displaystyle [a,b)&∈& \mathrm{Borel}(X) &&？ \\ \\ Q&∈& \mathrm{Borel}(X) && ？ \end{array}$

　

まあ直感的には明らかに「ボレル集合」なんですが

確証は無いので、きちんと確認する必要があります。

　

　

　

というわけで確認していくと

まず大前提として「位相空間」の定義は使えません。

　

$\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}$

　

これらは「開集合」でも「閉集合」でもないため

「開集合族・閉集合族」で「位相空間」を定義してるなら

「位相」からのアプローチでは除外される対象

　

　

つまり邪魔ものですから

その「位相空間」の枠組みではサポート対象外です。

　

　

ということは

当然それ以外の方法が必要になるわけなんですが

定義自体はそんなに多くありません。

　

$\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}A_n &∈&σ \end{array}$

　

なので使えそうなものを探っていくと

自然と「完全加法族」のこの性質に目が向きます。

　

　

　

その流れから

　

$\begin{array}{llllll} \displaystyle Q&∈& \mathrm{Borel}(X) &&？ \end{array}$

　

まず「有理数全体 $Q$ 」について考えていくと

　

$\begin{array}{ccc} q&∈&Q \\ \\ \displaystyle \{ q \}&∈&\mathrm{Closed \,\, Sets} \end{array}$

　

「点集合」が「閉集合」であること

「有理数全体と自然数全体の濃度」が同じであること

「ボレル集合」が「完全加法族」であることから

　

$\begin{array}{llllll} \displaystyle \{q_1\}∪\{q_2\}∪\cdots &=& \displaystyle \bigcup_{n=1}^{\infty}\{q_n\} \\ \\ &&\displaystyle \bigcup_{n=1}^{\infty}\{q_n\} &=&Q \end{array}$

　

このようにすれば

「有理数全体 $Q$ 」を構成できてしまうため

　

$\begin{array}{cccccc} \displaystyle \bigcup_{n=1}^{\infty}\{q_n\}&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}$

　

「有理数全体 $Q$ 」は

「ボレル集合」の条件を満たすと言えます。

　

　

　

同様に

こちらは少し工夫が必要ですが

「完全加法族」の定義を用いると

　

$\begin{array}{llllll} \displaystyle \left[ a,b-\frac{1}{n} \right]&\in&\mathrm{Closed \,\, Sets} \end{array}$

　

$\begin{array}{llllll} b-ε&<&b \\ \\ \displaystyle b-\frac{1}{n}&<&b \end{array}$

　

$\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty} \left[ a,b-\frac{1}{n} \right] &=&[a,b)\end{array}$

　

これもまたこのように構成できるので

「半開区間 $[a,b)$ 」は「ボレル集合」であると言えます。

（開区間と閉区間の共通部分からでも OK）