|| だいたい完全加法族とか測度の成立条件
証明はちゃんとやるとかなり大変なので紹介だけ
スポンサーリンク
目次
完全加法族「矛盾なく基本的な操作ができる枠組み」
カラテオドリの外測度「ルベーグ外測度を含むより広いやつ」
カラテオドリの可測条件「使いやすい可測の条件」
σ-有限「普通の測度が持ってる性質」
ジョルダン測度「測度の雛型(発想の出発点)」
有限加法的測度「カラテオドリの外測度より広いやつ」
直積測度「直積集合上での測度」
単調族「上限とか下限を定義できるやつ」
カラテオドリの基本定理「カラテオドリ外測度と完全加法族」
カラテオドリの拡張定理「外測度に入れ替えて良い根拠」
ホップの拡張定理「より広い範囲をカバーできるやつ」
コルモゴロフの拡張定理「無限直積集合でも測度は定義できる」
単調族定理「一意性の証明とかに使える定理」
単調収束定理「単調増加列と無限和集合の収束」
この記事を見る上で
この辺りの知識はほぼ必須なので
できれば理解しておきましょう。
カラテオドリの基本定理 Fundamental
|| 外測度上で可測な集合全体は完全加法族
「完全加法族 σ 」になる条件の1つ
\begin{array}{llllll} \displaystyle L_{μ^*}&=&\{ A∈2^X \mid A \,\, \mathrm{is} \,\, μ^*\text{-}\mathrm{Measurable} \} \\ \\ &=&\{ A⊂X \mid A \,\, \mathrm{is} \,\, μ^*\text{-}\mathrm{Measurable} \} \end{array}
「全体 X 」「カラテオドリ外測度 μ^* 」
「 μ^* 上で可測な集合全体 L_{μ^*} 」とすると
\begin{array}{ccccr} \displaystyle μ^*(∅)=0 &&→&& ∅∈L_{μ^*} \\ \\ \\ \displaystyle \begin{array}{r} \displaystyle A∈L_{μ^*} \\ \\ X∈L_{μ^*} \\ \\ X\setminus A∈L_{μ^*} \end{array} &&→&& A^c∈L_{μ^*} \\ \\ \\ \begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty}A_n \right)≤\displaystyle \sum_{n=1}^{\infty} μ^*(A_n) \end{array} &&→&&\displaystyle \bigcup_{n=1}^{\infty}A_n∈L_{μ^*} \end{array}
要はこういう感じになるってことを
この定理は主張しています。
(ルベーグ外測度を一般化した結果)
証明の概要
証明は「可測」条件を使うだけ
\begin{array}{llllll} \displaystyle μ^*(S)&=&μ^*(S∩A)+μ^*(S∩A^c) \\ \\ &=&μ^*(S∩A^c)+μ^*(S∩(A^c)^c) \end{array}
そもそも「外測度 μ^* 」の定義が明確で
\begin{array}{llllll} \displaystyle μ^*(∅)&=&0 \end{array}
「可測の条件」
「可測集合全体 L_{μ^*} 」の定義も明らかなので
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}A_n&∈&L_{μ^*} \end{array}
これはちょっと面倒ですが
「空集合」「補集合」についてはすぐに示せます。
(基本的にルベーグ外測度上の話と同様)
可測集合の和集合
ここでは長くなるので省略しますが
「可測集合の和」は「可測集合」になります。
\begin{array}{llllll} \displaystyle A∪B&∈&L_{μ^*} \end{array}
この結果は当然のように感じますが
実はこれを示すのはちょっと面倒
なので詳細はここでは語りません。
「可測集合の可算和」もまた同様
「有限の可算」「数学的帰納法」「極限」から
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}A_n&∈&L_{μ^*} \end{array}
ちょっと面倒な手順を踏むと
「カラテオドリの条件」より
「可測集合」だと言えるので
\begin{array}{rcr} && ∅∈L_{μ^*} \\ \\ A∈L_{μ^*}&→&A^c∈L_{μ^*} \\ \\ A_1,A_2,...,A_n,...∈L_{μ^*}&→& \displaystyle \bigcup_{n=1}^{\infty}A_n∈L_{μ^*} \end{array}
結果、以上の条件が満たされることから
「外測度 μ^* 上で可測な集合全体 L_{μ^*} 」は
「完全加法族である」と言えます。
カラテオドリの拡張定理 Caratheodory
|| ジョルダン測度とルベーグ測度の関係
「前測度」から「測度」を作れる条件の話
\begin{array}{ccc} \displaystyle X & \mathrm{Ring} & μ \\ \\ &↓&↓ \\ \\ X & σ(\mathrm{Ring}) & μ^* \end{array}
「拡張」という形で
\begin{array}{cc} \forall A\in \mathrm{Ring} & μ(A)=μ^*(A) \end{array}
この定理は「測度の存在」を保証します。
拡張 Extension
「制限」とは逆の感覚の操作
(制限されたもの → 元は広い)
\begin{array}{ccc} \mathrm{Field}&⊂&σ(\mathrm{Field}) \\ \\ A_{\mathrm{part}}&⊂&A \end{array}
\begin{array}{llllll} \displaystyle f&:&A&→&B \\ \\ f|_{A_{\mathrm{part}}}&:&A_{\mathrm{part}}&→&B_{\mathrm{part}} \end{array}
この「制限 f|_{A_{\mathrm{part}}} 」操作の逆
つまり「制限前の関数 f 」が
「 f|_{A_{\mathrm{part}}} から見た」「拡張」になります。
σ-有限 sigma-finite
『測度の一意性を保証できる条件』のこと
\begin{array}{ccccccccc} \mathrm{non} & σ\text{-}\mathrm{finite} \\ \\ 〇& × & \begin{array}{c} \mathrm{Only} \,\, 0 \,\, \mathrm{or} \,\, \infty \end{array} \end{array}
「無限じゃないもの」の存在を保証する条件のことで
これにより「測度の一意性」が保証されます。
(これは詳細を知らないと分かりにくいです)
証明の概要
これの証明には多くの知識を要求されますが
\begin{array}{ccc} \displaystyle X & \mathrm{Ring} & μ \\ \\ &↓&↓ \\ \\ X & σ(\mathrm{Ring}) & μ^* \end{array}
基本的に主張したいことはこれだけです。
\begin{array}{ccc} μ\Bigl( [a,b) \Bigr) &=& b-a \end{array}
「前測度(ジョルダン測度の一般化)の存在」から
\begin{array}{ccc} A&⊂&\displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ μ^*(A)&=&\displaystyle\inf\left\{ \sum_{n=1}^{\infty}μ(A) \right\} \end{array}
「前測度の拡張」として
「外測度(ルベーグ測度)の存在」を導ける。
このために定義を確認していくのが
この定理の証明になります。
ホップの拡張定理 Hopf
|| カラテオドリの拡張定理を一般化したやつ
「有限加法族」上の「有限加法的測度」が
「完全加法性を持つ」場合の話
\begin{array}{ccc} &\mathrm{Extension}& \\ \\ (X,F,μ) &→& (X,σ(F),μ^*) \end{array}
だいたい「カラテオドリの拡張定理」と同様です。
「前測度」に限定された話ではなくなるので
こちらの方が使い勝手は良いかもしれません。
有限加法族 Finitely Additive Class
「完全加法族」の条件を緩めたやつ
\begin{array}{rcr} && ∅\in F \\ \\ A\in F &→& A^c∈F \\ \\ A,B∈F &→& A∪B\in F \end{array}
「完全加法族じゃ定義できない」
そういう「集合関数」を考えるためのもの。
(ジョルダン測度はこれの上で定義されます)
有限加法的測度 Finitely Additive
「有限回の加法だけ」制限されてる測度のこと
だいたい「ジョルダン測度」のことを指します。
\begin{array}{llllll} \displaystyle μ(∅)&=&0 \end{array}
\begin{array}{ccl} \displaystyle \left( \begin{array}{ccc} && A_i,A_j∈σ \\ \\ \displaystyle i≠j &→&A_i∩A_j=∅ \end{array} \right) \\ \\ ↓ \\ \\ μ(A_i∪A_j)=μ(A_i)+μ(A_j) \end{array}
「完全加法的測度」を「測度」と言い
これはそれよりも条件としては緩いです。
(完全加法性から有限加法性は導ける)
完全加法性 Sigma Additivity
「図形の足し算」を考えるために必要な

「図形が被ってない」時の基本的な性質
\begin{array}{llllll} \begin{array}{c} A_1,A_2,A_3,...∈F \\ \\ \displaystyle\bigcup_{n=1}^{\infty}A_n∈F \\ \\ i≠j \,\,⇒\,\, A_i∩A_j≠∅ \end{array} &&→&&\displaystyle μ\left( \bigcup_{n=1}^{\infty}A_n \right)= \sum_{n=1}^{\infty}μ(A_n) \end{array}
「有限加法族 F 」上では
「無限和集合」は「有限加法族」上の要素に制限されます。
(有限加法的測度で大きさが分かる範囲に合わせるため)
証明の概要
だいたい「カラテオドリの拡張定理」と同じですが
「前測度」が前提に来ないので
\begin{array}{llllll} \begin{array}{c} A_1,A_2,A_3,...∈F \\ \\ i≠j \,\,⇒\,\, A_i∩A_j≠∅ \end{array} &&→&&\displaystyle μ\left( \bigcup_{n=1}^{\infty}A_n \right)= \sum_{n=1}^{\infty}μ(A_n) \end{array}
「完全加法性」を確認する必要があります。
(わりと大変なので詳細は別の記事で)
コルモゴロフの拡張定理 Kolmogorov
|| 直積を無限回行っても直積測度は測度なのか
「直積」と「無限」についての定理です。
\begin{array}{ccc} μ^n(A^n) &&→ && μ^{\infty} (A^{\infty}) \end{array}
「無限直積集合」と「測度」の関係
\begin{array}{lclcc} A^n &→& μ^n(A^n) &&〇 \\ \\ A^{\infty} &→& μ^{\infty}(A^{\infty}) &&? \end{array}
これをこの定理は説明します。
(コインを無限回振った時とかの話)
直積集合 Product Set
「対・組」を要素に持つ集合のこと
\begin{array}{ccc} A\times B &=&\{ (a,b) \mid a\in A ∧ b\in B \} \end{array}
「長方形」「直方体」「配列」等々
こういうのを厳密に定義してるやつがこれ。
直積測度 Product Measure
「長さ×長さ=面積」みたいな
「直積集合」に定義できる「測度」のこと
\begin{array}{ccc} μ_X\times μ_Y(A_X\times A_Y) &=& μ_X(A_X)μ_Y(A_Y) \end{array}
「測度空間」同士の「直積測度空間」は
「測度空間」の条件を満たします。
(詳細は長くなるので別記事で)
無限直積集合 Infinite Direct Product
「 \infty-組」を要素に持つ集合のこと
\begin{array}{ccc} (x_1,x_2,...,x_n,...) &\in& X\times X \times \cdots \end{array}
厳密には「写像」で定義されています。
(詳細はちょっと長いので別記事で)
\begin{array}{ccc} \displaystyle\prod_{λ\in Λ} X_λ &=&\displaystyle \left\{ f \mid \forall λ\in Λ \,\, f(λ)\in X_λ \right\} \end{array}
「集合論」の知識が無いとこの辺りは分かりません。
(写像 f は組 (x_1,...,x_n,...) だと思って良いです)
証明の概要
この証明には特殊な操作が多く
特に「無限」の扱いが非常に大変です。
\begin{array}{lcl} μ^{n}(A^n)&=&μ^{n+1}(A^n\times R) \\ \\ &↓ \\ \\ μ^{n}(A^n)&=&μ^{\infty}(A^n\times R^{\infty}) \end{array}
特に「拡張定理」に寄せるアプローチでは
「無限直積集合」について
\begin{array}{lcl} A&⊂&R \\ \\ A\times R &⊂&R^2 \\ \\ &\vdots \\ \\ A\times R^n &⊂&R^{n+1} \\ \\ A\times R^{\infty} &⊂&R^{\infty} \end{array}
「拡張」を考えるために
「柱状集合」と呼ばれる集合 C を考える必要があって
\begin{array}{rcr} && ∅ \in C \\ \\ A \in C &→& A^c \in C \\ \\ A,B \in C &→& A∪B \in C \end{array}
これにより
「有限」の話に落とし込んでいくわけですが
\begin{array}{ccc} \forall A\in \mathrm{Borel}(R^n)&μ^{n}(A)=μ^{\infty}(A\times R^{\infty}) \end{array}
\begin{array}{ccc} μ^{\infty}&:& \mathrm{Borel}(R^n) &\to& [0,\infty] \end{array}
この過程で
何度も「無限」を意識する必要があるので
よく ほんとか? って気分になります。
単調族定理 Monotone Class Theorem
|| 完全加法族になる条件の一つ
「有限加法族 F を含む最小の単調族 M 」は
「 F から作れる完全加法族 σ(F) 」になる
\begin{array}{llllll} F⊂σ&&→&&σ(F) \\ \\ \displaystyle F⊂M&&→&&M(F) \\ \\ \min (M(F)) &&→&&M_{\mathrm{min}}(F) \end{array}
\begin{array}{llllll} \displaystyle σ(F)&=&M_{\mathrm{min}}(F) \end{array}
「有限加法族 F 」と
「完全加法族 σ 」の違い
\begin{array}{c} \begin{array}{llllll} \displaystyle μ \left( \bigcup_{i=1}^{n}A_i \right)&=&\displaystyle \sum_{i=1}^{n}μ(A_i) \end{array} \\ \\ ↓ \\ \\ \displaystyle \begin{array}{llllll} \displaystyle μ \left( \bigcup_{i=1}^{\textcolor{pink}{\infty}}A_i \right)&=&\displaystyle \sum_{i=1}^{\textcolor{pink}{\infty}}μ(A_i) \end{array} \end{array}
これを知ってれば
この定理の主張はわりと直感的に分かると思います。
(証明は長くなるので別の記事で)
単調族 Monotone Class
「極限」の集合論的な感覚を表現したもの
(以下の性質を満たす集合族 M のこと)
\begin{array}{llllll} \displaystyle X&≠&∅ \end{array}
\begin{array}{llllll} \displaystyle \{A_1,A_2,A_3,...\}&⊂&M&⊂&2^X \\ \\ \{B_1,B_2,B_3,...\}&⊂&M&⊂&2^X \end{array}
\begin{array}{llllll} \displaystyle A_1⊂A_2⊂A_3⊂\cdots &&→&&\displaystyle \bigcup_{n=1}^{\infty}A_n∈M \\ \\ B_1⊃B_2⊃B_3⊃\cdots &&→&&\displaystyle \bigcap_{n=1}^{\infty}B_n∈M \end{array}
「測度」が持っていて欲しい性質の1つで
分かりやすく「極限」の性質を表しています。
単調収束定理 Monotone Convergence
|| 単調増加と測度の関係についての定理
「単調増加列」と「無限和」が用意された時の話
\begin{array}{ccc} A_1,A_2,A_3,...,A_n,... \in σ \\ \\ A_1⊂A_2⊂\cdots⊂A_n⊂\cdots \end{array}
↓
\begin{array}{ccc} \displaystyle μ \left( \bigcup^{\infty}_{n=1} A_n \right) &=&\displaystyle \lim_{n\to\infty} μ(A_n) \end{array}
これにより
「単調増加列」を構成できれば
「無限和」と「収束先の集合」の関係が
\begin{array}{ccc} \displaystyle\bigcup^{\infty}_{n=1} A_n &=& A_{\infty} \end{array}
こうなることを保証できます。
(無限和集合の測度を簡単に考えられる)
単調収束定理の証明
これはかなり直感的な話で
\begin{array}{ccc} A_n&⊂& \displaystyle \bigcup_{n=1}^{k}A_n \end{array}
「単調増加」と「収束先」を考えた時
自然な結論として導かれるものになります。
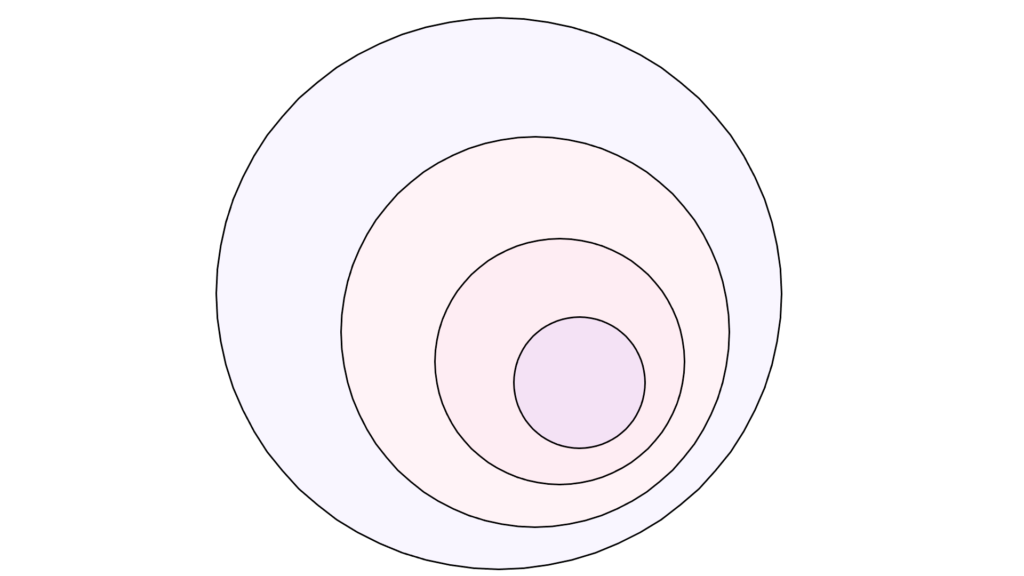
実際、画像のようなイメージの話なので
この性質を確認していけば自然と証明できます。
極限集合と無限和
これは「極限集合」を考えると簡単で
\begin{array}{ccc} \displaystyle\bigcup_{m=1}^{n} A_m&⊂&A_n \\ \\ \displaystyle\bigcup_{m=1}^{\infty} A_m&=&\displaystyle\bigcup_{m=n}^{\infty} A_m \end{array}
「単調増加列」の「有限範囲の性質」から
\begin{array}{ccc} \displaystyle \bigcap_{n=1}^{\infty}\bigcup_{m=n}^{\infty} A_m &=& \displaystyle \bigcap_{n=1}^{\infty}\bigcup_{m=1}^{\infty} A_m &=& \displaystyle \bigcup_{m=1}^{\infty} A_m\end{array}
こうなることはすぐに導けます。
単調減少列の収束定理
「単調増加列」では ↑ みたいになるように
\begin{array}{ccc} A_1,A_2,A_3,...,A_n,... \in σ \\ \\ A_1⊃A_2⊃\cdots⊃A_n⊃\cdots \end{array}
↓
\begin{array}{ccc} \displaystyle μ \left( \bigcap^{\infty}_{n=1} A_n \right) &=&\displaystyle \lim_{n\to\infty} μ(A_n) \end{array}
実は「単調減少列」では
これはこのようになります。
単調減少列における収束定理の証明
「単調減少列」だと
\begin{array}{ccc} \displaystyle \bigcap_{n=1}^{m} A_n &=& \displaystyle A_m \end{array}
「有限範囲の性質」として
こういう関係が考えられるので
\begin{array}{ccc} \forall k & A_n⊃A_{n+k} \\ \\ \forall k & x\in A_n ⇐ x \in A_{n+k} \end{array}
\begin{array}{ccc} \displaystyle \bigcup_{m=n}^{\infty} A_m &=&A_n \end{array}
「無限和集合」についての性質と合わせると
後は「極限集合」の定義さえ理解していれば
\begin{array}{ccc}\displaystyle \bigcap_{n=1}^{\infty}\bigcup_{m=n}^{\infty} A_m &=& \displaystyle \bigcap_{n=1}^{\infty} A_n &=&\displaystyle \bigcap_{n=m}^{\infty} A_n&=&\displaystyle \bigcup_{m=1}^{\infty}\bigcap_{n=m}^{\infty} A_n \end{array}
これは当然の帰結として導かれます。
