|| 実数の集合についてのあれこれ
「実数」の「完全加法族」のこと
スポンサーリンク
事前知識
測度空間「ボレル集合を考える理由」
完全加法族「矛盾なく足し算ができるやつ」
極限「実数が持つ近付けるっていう感覚の形式表現」
区間「実数を集合で表現する代表的な方法の1つ」
開集合「実数で定義される区間を厳密に定義するやつ」
位相空間「連続を矛盾なく定義できる枠組み」
目次
ボレル集合「実数バージョンの完全加法族」
こいつについて厳密には理解できないと思います。
ただ、これ自体はそんな難しいものではないので
感覚的にはなんとなく分かるかと。
ボレル集合 Borel Set
|| 実数の測度を考える時に出てくるやつ
「実数」上で「普通の操作ができる集合」のこと
(いろんなものが含まれるように調整されてる)
\begin{array}{llllll} \displaystyle (-\infty,\infty)&→&(0,1),(-1,2),\cdots \\ \\ &→&\{0\},N,Q,(0,1),[0,2),\cdots \end{array}
\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \\ \\ O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \\ \\ σ\Bigl( O(X)\Bigr) &\mathrm{is} & σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}
矛盾が出ないよう
そのまま「完全加法族」として定義されています。
\begin{array}{llllll} \displaystyle \mathrm{Borel}(X)&=&σ\Bigl( O(X)\Bigr) \end{array}
この \mathrm{Borel}(X) が「ボレル集合族」で
この「ボレル集合族の要素」が「ボレル集合」になります。
(具体的には区間とか点集合とかのこと)
ボレル集合族の中身
この時点じゃなんで?って話かもしれませんが
\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}
こいつは「開集合」と「閉集合」の両方と
「任意の区間」「点の集まり」を中身に持ちます。
ボレル集合の役割
これの役割を簡単に言うなら
「区間」を「矛盾なく使うためのもの」って感じで
\begin{array}{cclcccll} \displaystyle (a,b)&=&\{ x∈R \mid a<x<b \} \\ \\ [a,b]&=&\{ x∈R \mid a≤x≤b \} \\ \\ (a,b]&=&\{ x∈R \mid a<x≤b \} \\ \\ [a,b)&=&\{ x∈R \mid a≤x<b \} \end{array}
「ボレル集合族(ボレル集合の集まり)」は
そのために整備された「集合の集まり」になります。
なので順番は
「区間・点・それらの組み合わせ」が先
\begin{array}{llllll} \displaystyle \begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array} &→&\mathrm{Borel}(X) \end{array}
「ボレル集合族 \mathrm{Borel}(X) 」の定義は
これを含むように調整されています。
位相空間が保証すること
問題なく「極限」の操作ができる
「開集合 → 開集合」「閉集合 → 閉集合」になる
そういったことを保証するのが「位相空間」の役割で
\begin{array}{llllll} \displaystyle (X,O) \end{array}
\begin{array}{llllll} \displaystyle \lim_{ε\to0} ε &=&0 \end{array}
具体的には
「集合の操作」を制限することで
\begin{array}{cccccccccll} \displaystyle && A&⊂&S&⊂&B \\ \\ ∅&⊂& A&⊂&S&⊂&B&⊂&X \end{array}
必ず「大きい値と小さい値が分かる」
つまり「より大きい・小さい値が存在する」
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}&&〇 \\ \\ \displaystyle \bigcap_{n=1}^{\infty}&&× \\ \\ \displaystyle \bigcup_{n=1}^{k}&&〇 \end{array}
「この操作はしていい」
「この操作では矛盾が出る」
みたいなことをこれは保証しています。
開集合とは
その存在を必ず考えなければならないもの
\begin{array}{llllll} \displaystyle 1&<&a&<&2 \end{array}
それが「開集合」という概念で
\begin{array}{llllll} \displaystyle \mathrm{Ball}(α,ε)&=&\{ x∈X \mid |x-α|<ε \} \\ \\ &=&(α-ε,α+ε) \end{array}

「点の実態(見える大きさのある点)」
という図形の直感的な性質とか
\begin{array}{llllll} \displaystyle (0,3)&=&\{ x \mid 0<x<3 \} \end{array}
この集合の境界はどうなってんの?とか
そういうのを厳密に定義する時に使われます。
それと変な感じがしますが
\begin{array}{llllll} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \end{array}
これは「開集合の補集合」である
「閉集合」とセットの概念になります。
(片方だけではカバー範囲が狭い上に使いにくい)
開集合のややこしい定義
「 X の開集合 O 」という概念は
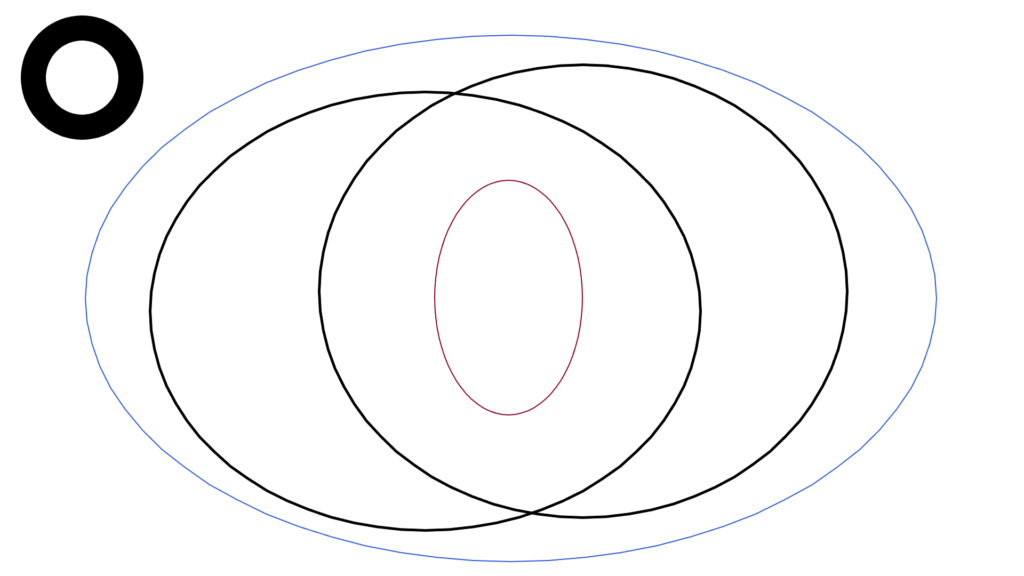
\begin{array}{llllll} \displaystyle && &&O&⊂&X \\ \\ && \mathrm{Ball}(α,ε)&⊂&O \\ \\ α&∈&\mathrm{Ball}(α,ε) \end{array}
O の中の任意の点 α∈\mathrm{Ball}(α,ε)
これを持つ集合 \mathrm{Ball}(α,ε) が常に内側にある
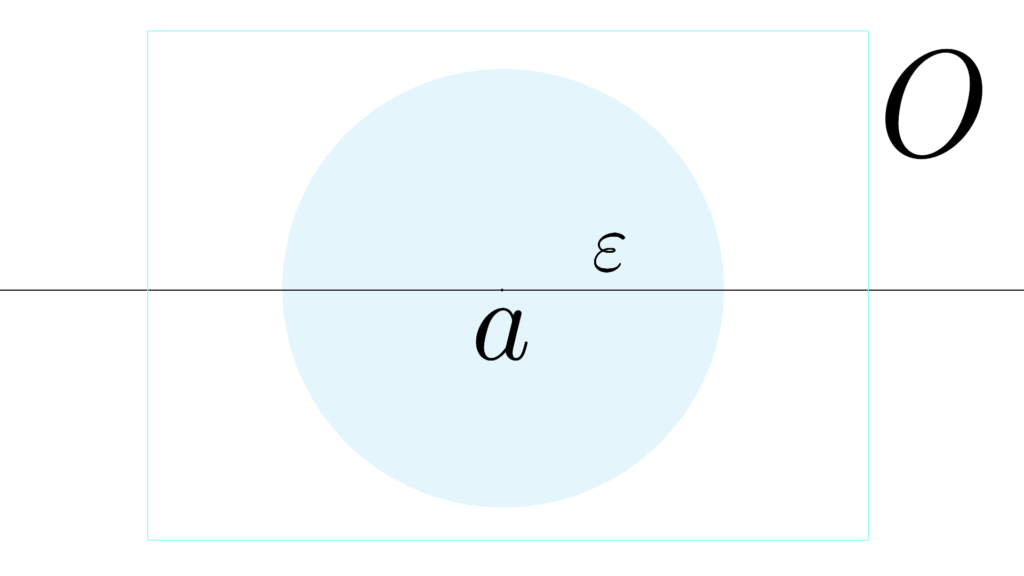
\begin{array}{llllll} \displaystyle \mathrm{Ball}(α,ε)&⊂&O \end{array}
これが「 O の全ての点 α で成り立つ」
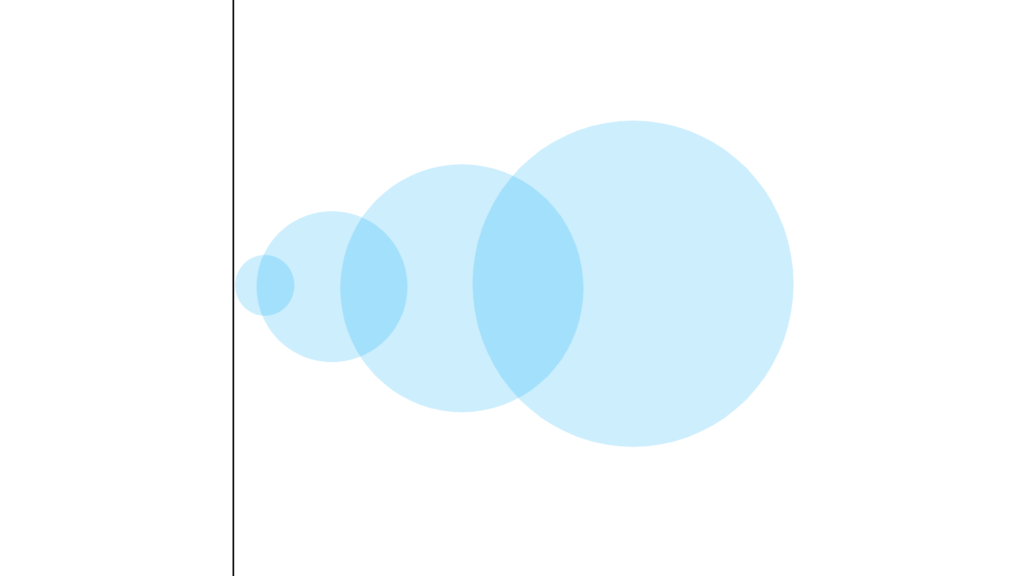
そういう集合 O のことを指していて
主に「境界を含まないとは」とか
「ある点 α のすっごい近くにある」とか
そういう感じのことを厳密に説明するとき使われます。
完全加法族が保証すること
いろんな操作が問題なくできる
ということをこれは保証しています。
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ S∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A,B∈σ&\to&\displaystyle A\setminus B∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n ∈σ \end{array} \right) \end{array}
具体的には
こういった「集合の基本操作」が
「矛盾を導かない」ということが保証できます。
今回の場合
\begin{array}{llllll} \displaystyle (0,2)∪(1,3)&=&(0,3) \\ \\ (0,2)∩(1,3)&=&(1,2) \end{array}
「区間」という「集合」について
問題なくこういった操作を行える
\begin{array}{ccc} [a,b)&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}
あるいはこういったものも含まれる
というようなことを保証するのに
この考え方が使われる感じです。
ボレル集合の定義の解説
「位相空間 (X,O) 」上であること
\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \end{array}
「 X から生成された開集合全体 O(X) 」
\begin{array}{cccl} O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \end{array}
「 O(X) から生成された完全加法族 σ\Bigl( O(X)\Bigr) 」
\begin{array}{cccl} σ\Bigl( O(X)\Bigr) &\mathrm{is} & σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}
これらを一つずつ解説していくと
位相空間だと
まず「位相空間」についてですが
(長くなるので詳細は省きます)
\begin{array}{cccl} \displaystyle (X,O) &\mathrm{is} & \mathrm{Topology \,\, Space} \end{array}
\begin{array}{llllll} \displaystyle O&⊂&2^X \end{array}
これは特定の「操作」によって
『ある操作が可能であるか』に『変化が無い』
つまり「構造の変化が起きない」ことを保証していて
具体的には
以下のような操作を行った時
\begin{array}{rcccc} \displaystyle A∩B∈τ&&〇 \\ \\ \displaystyle\bigcap_{i∈I}A_i∈τ&&× \\ \\ \\ A∪B∈τ&&〇 \\ \\ \displaystyle\bigcup_{i∈I}A_i∈τ&&〇 \end{array}
必ず「開集合 → 開集合」になる操作があって
その操作のみを許可する感じです。
(許可された操作で作ったものだけで構成)
ある集合 X から作られた開集合
「 X から生成された開集合全体 O(X) 」について
\begin{array}{cccl} O(X) &\mathrm{is} & \mathrm{Open \,\, Sets} & \mathrm{generated \,\, from} \,\, X \end{array}
これは大雑把にしか記述できませんが
\begin{array}{llllll} \displaystyle X&⊂&R=(-\infty,\infty) \end{array}
↓
\begin{array}{ccc} \displaystyle (0,1)&⊂&X \\ \\ (1,3)&⊂&X \\ \\ (a,b)&⊂&X \\ \\ &\vdots& \end{array}
要はこういう感じの話で
「全体 X から」作ることができる
「開集合だけ」で構成されていることを意味します。
最終工程である「完全加法族」
これが「補集合」を中身に含むので
\begin{array}{llllll} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \end{array}
「閉集合全体」もまた
最終的には「ボレル集合族」の中に含まれます。
開集合 O(X) から作られる完全加法族
これも考え方は似たようなもので
\begin{array}{cc} σ\text{-}\mathrm{Additive} &\mathrm{generated \,\, from} \,\, O(X) \end{array}
O(X) の要素のみに
\begin{array}{rcr} \displaystyle O(X)&⊂&σ\Bigl( O(X)\Bigr) \\ \\ A∈O(X)&→&A∈σ\Bigl( O(X)\Bigr) \end{array}
「完全加法族」の定義に則って
↓ の操作を加えると
\begin{array}{rcr} \displaystyle A∈O(X)&→&A^c∈σ\Bigl( O(X)\Bigr) \\ \\ A_1,A_2,...,A_n,...∈O(X)&→&\displaystyle \bigcup_{n=1}^{\infty}A_n∈σ\Bigl( O(X)\Bigr) \end{array}
この σ\Bigl( O(X)\Bigr) が出来上がります。
補足しておくと
この過程で「補集合」を含めることになるので
\begin{array}{ccc} \displaystyle (\mathrm{Open\,\,Set})^c&=&\mathrm{Closed\,\,Set} \\ \\ (\mathrm{Closed\,\,Set})^c&=&\mathrm{Open\,\,Set} \end{array}
「開集合の補集合」は「閉集合」であり
「閉集合の補集合」は「開集合」であることから
\begin{array}{ccc} \displaystyle \mathrm{Open\,\,Set}&∈&σ\Bigl( O(X)\Bigr) \\ \\ \mathrm{Closed\,\,Set}&∈&σ\Bigl( O(X)\Bigr) \end{array}
「位相空間」を「開集合族」で定義しても
その「補集合」である「閉集合族」で定義しても
これの中身は同じになります。
ボレル集合と区間
以上の「ボレル集合族の定義」は
『良い感じに調整された定義』です。
\begin{array}{llllll} \displaystyle \mathrm{Borel}(X)&=&σ\Bigl( O(X)\Bigr) \end{array}
なので問題を含んでいる可能性があります。
(結論の先取りですが問題はありません)
とまあそういうわけですから
念のため「ボレル集合」の定義に問題が無いか
\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}
ここできちんと確認しておきます。
開集合と閉集合
確認する上で必要になる以下に関して
\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Open\,\,Sets} \\ \\ [a,b]&∈&\mathrm{Closed\,\,Sets} \\ \\ \\ \{a\}&∈&\mathrm{Closed\,\,Sets} \\ \\ N&∈&\mathrm{Closed\,\,Sets} \end{array}
ちゃんとやりたいんですが
厳密な話をするとなると
「開集合」を深堀する必要があるので
\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}
とりあえずこの記事では
これらについては特に言及しません。
というわけで
以上のことはひとまず飲み込んで
「ボレル集合」について確認すると
\begin{array}{llllll} \displaystyle \mathrm{Open\,\,Set}&∈& \mathrm{Borel}(X) \\ \\ \mathrm{Closed\,\,Set}&∈& \mathrm{Borel}(X) \end{array}
「開集合」「閉集合」は
間違いなく「ボレル集合」であることから
\begin{array}{ccc} \displaystyle (a,b)&∈& \mathrm{Borel}(X) \\ \\ [a,b]&∈& \mathrm{Borel}(X) \\ \\ \\ \{a\}&∈& \mathrm{Borel}(X) \\ \\ N&∈& \mathrm{Borel}(X) \end{array}
ひとまず
これらは「ボレル集合」であると言えます。
開集合でも閉集合でもないもの
問題となるのは以下のような
「開集合」「閉集合」ではないもので
\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}
これらが「ボレル集合」であるかどうかは
この時点ではまだ分かっていません。
\begin{array}{ccc} \displaystyle [a,b)&∈& \mathrm{Borel}(X) &&? \\ \\ Q&∈& \mathrm{Borel}(X) && ? \end{array}
まあ直感的には明らかに「ボレル集合」なんですが
確証は無いので、きちんと確認する必要があります。
というわけで確認していくと
まず大前提として「位相空間」の定義は使えません。
\begin{array}{ccc} [a,b)&\not\in&\mathrm{Open\,\,Sets} \\ \\ [a,b)&\not\in&\mathrm{Closed\,\,Sets} \\ \\ \\ Q&\not\in&\mathrm{Open\,\,Sets} \\ \\ Q&\not\in&\mathrm{Closed\,\,Sets} \end{array}
これらは「開集合」でも「閉集合」でもないため
「開集合族・閉集合族」で「位相空間」を定義してるなら
「位相」からのアプローチでは除外される対象
つまり邪魔ものですから
その「位相空間」の枠組みではサポート対象外です。
ということは
当然それ以外の方法が必要になるわけなんですが
定義自体はそんなに多くありません。
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}A_n &∈&σ \end{array}
なので使えそうなものを探っていくと
自然と「完全加法族」のこの性質に目が向きます。
その流れから
\begin{array}{llllll} \displaystyle Q&∈& \mathrm{Borel}(X) &&? \end{array}
まず「有理数全体 Q 」について考えていくと
\begin{array}{ccc} q&∈&Q \\ \\ \displaystyle \{ q \}&∈&\mathrm{Closed \,\, Sets} \end{array}
「点集合」が「閉集合」であること
「有理数全体と自然数全体の濃度」が同じであること
「ボレル集合」が「完全加法族」であることから
\begin{array}{llllll} \displaystyle \{q_1\}∪\{q_2\}∪\cdots &=& \displaystyle \bigcup_{n=1}^{\infty}\{q_n\} \\ \\ &&\displaystyle \bigcup_{n=1}^{\infty}\{q_n\} &=&Q \end{array}
このようにすれば
「有理数全体 Q 」を構成できてしまうため
\begin{array}{cccccc} \displaystyle \bigcup_{n=1}^{\infty}\{q_n\}&∈& \mathrm{Borel}(X) \\ \\ Q&∈& \mathrm{Borel}(X) \end{array}
「有理数全体 Q 」は
「ボレル集合」の条件を満たすと言えます。
同様に
こちらは少し工夫が必要ですが
「完全加法族」の定義を用いると
\begin{array}{llllll} \displaystyle \left[ a,b-\frac{1}{n} \right]&\in&\mathrm{Closed \,\, Sets} \end{array}
\begin{array}{llllll} b-ε&<&b \\ \\ \displaystyle b-\frac{1}{n}&<&b \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty} \left[ a,b-\frac{1}{n} \right] &=&[a,b)\end{array}
これもまたこのように構成できるので
「半開区間 [a,b) 」は「ボレル集合」であると言えます。
(開区間と閉区間の共通部分からでも OK)
