|| 点の位置を決定するためのあれこれ
座標を扱うやつらの総称
スポンサーリンク
目次
座標「点の位置を決定するための数」
座標系「点の位置を確定させるものの総称」
直交座標系「 x,y を直接決める(よく見る)」
極座標系「長さ r と角度 θ で x,y を両方決定」
線形空間「ベクトルが使えることを保証する枠」
ベクトル「1点が持ってる方向的な感覚」
ノルム「長さの概念を一般化したやつ」
内積「ベクトルの掛け算的な操作」
四元数「内積と外積の由来」
行列「ベクトルのベクトルみたいなやつ」
線形写像「点をどこにでも移動させられる」
行列式「逆行列で出てくるやつ」
関数行列「ヤコビアンとかいうやつ」
座標 Coordinate
|| 位置を確定するために必要な数
『位置を表現するための数』のこと
\begin{array}{cccc} (x,y)&&(x,y,z) \\ \\ (a,b)&&(a,b,c) \\ \\ \displaystyle (0,0) && (0,0,0) \end{array}
「数の組・ペア \mathrm{Coordinates} 」も
「その中の1つ \mathrm{Coordinate} 」も
日本語ではどちらも「座標」です。
座標系 Coordinate System
|| 点の位置を決定する方法を与えるもの
「点の座標」を示す「数字の意味」を
「決める方法」のことを座標系と言います。
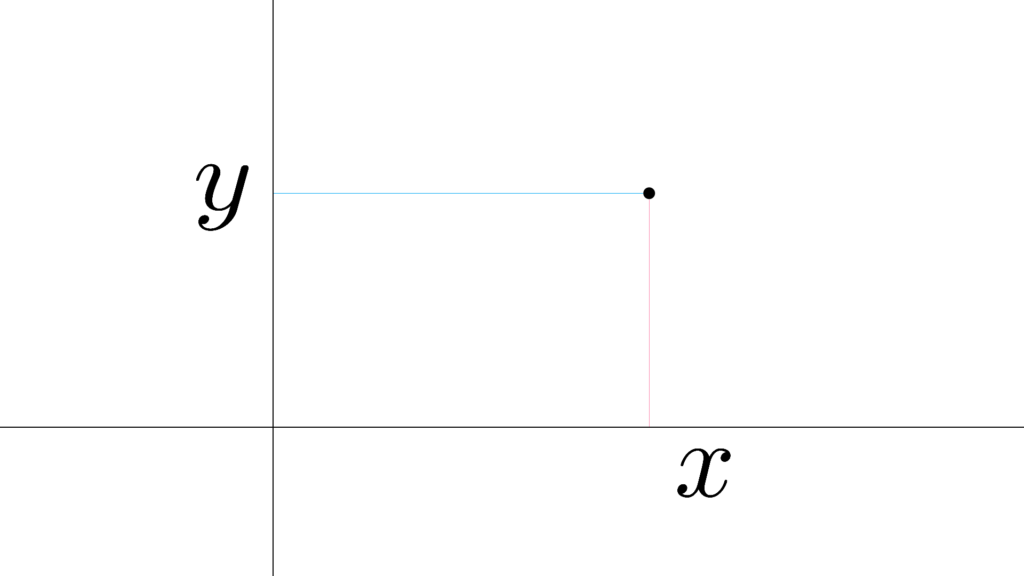
よく見る ↑ の画像のやつの名前は
「直交座標系(デカルト座標系)」です。
座標と座標系
「座標」は『点の位置を表現する数の組』のこと
\begin{array}{llllll} \displaystyle (0,0) && (x,y) \end{array}
「座標系」は『座標の意味を決めるもの』のことで
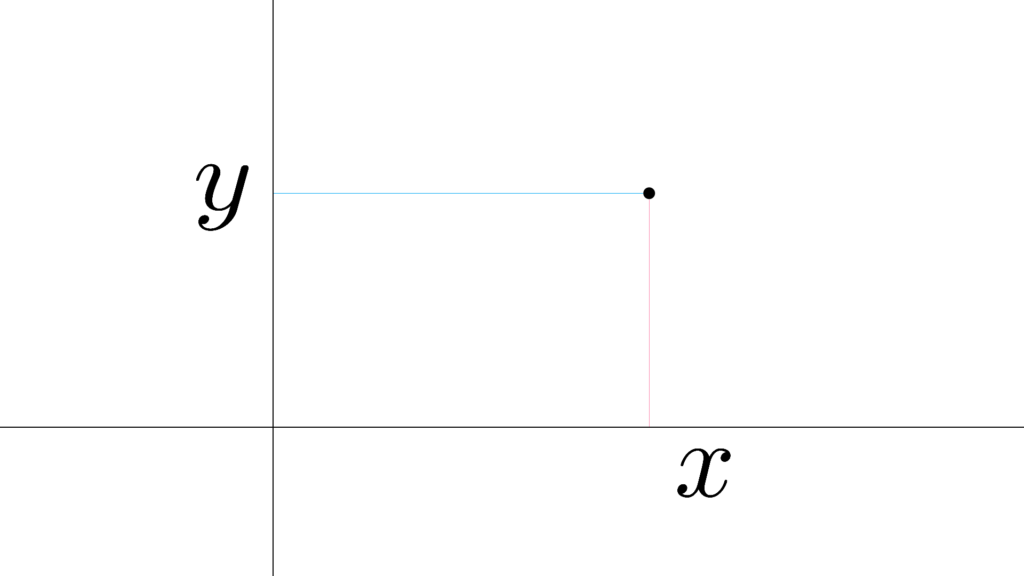
「原点・座標軸の取り方」といった
『図形を視覚化する』操作は
「座標系」が担当する役割になります。
直交座標系 Rectangular
|| 最も直感的な座標の決め方
「デカルト座標系」とも呼ばれます。
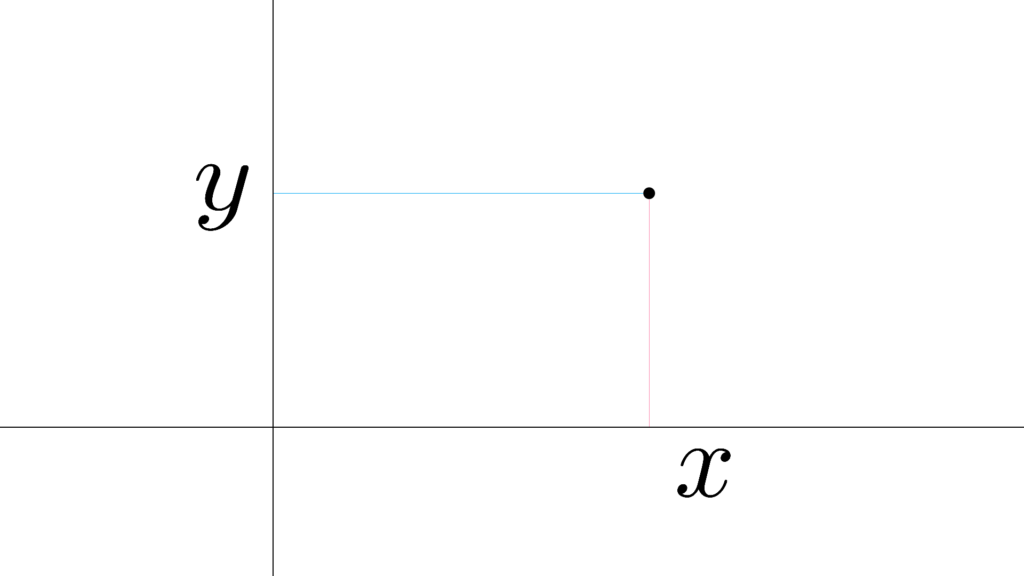
まあこれは説明不要でしょう。
「座標」って言ったらだいたいこれですし。
極座標系 Polar
|| よく使う座標系その2
「長さ r 」と「角度 θ 」で決める方法
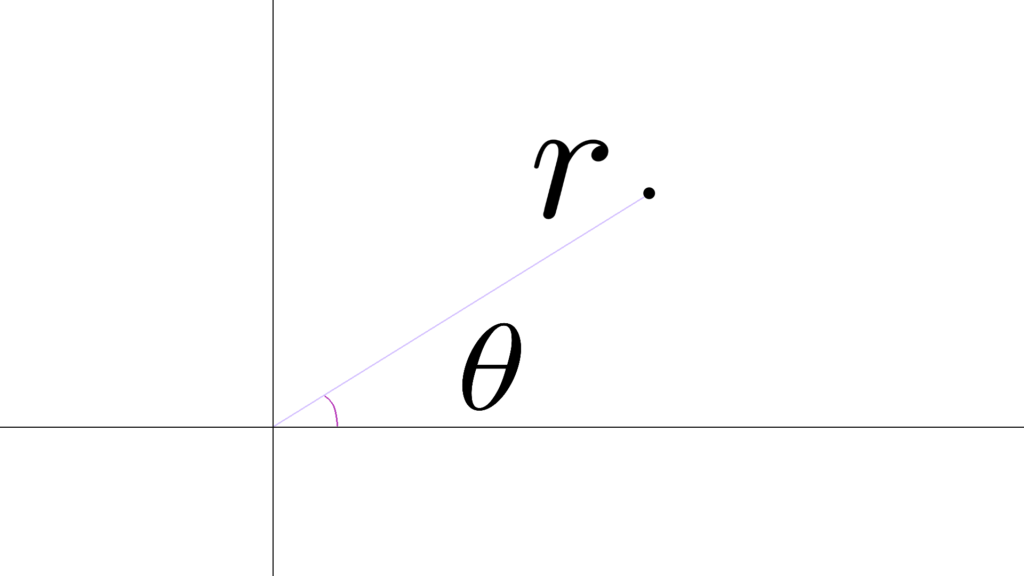
\begin{array}{llllll} \displaystyle x&=&r\cos θ \\ \\ y&=&r\sin θ \end{array}
\begin{array}{llllll} \displaystyle r&=&\displaystyle \sqrt{x^2+y^2} \end{array}
「複素平面」の話なんかで出てくるやつで
主に『回転』操作を行う時によく使われます。
空間での座標系
「空間(3次元)」でも
『直交座標系』は当然として
(x,y,z)
『極座標系』の考え方を使った
「円筒座標系( z だけ直交座標系)」ってやつと
\begin{array}{llllll} \displaystyle x&=&r\cos θ \\ \\ y&=&r\sin θ \\ \\ z&=&z \end{array}
「球面座標系(極座標系の拡張)」ってやつがあります。
\begin{array}{llllll} \displaystyle x&=&r\cos θ\sin φ \\ \\ y&=&r\sin θ \sin φ \\ \\ z&=&r\cos φ \end{array}
この辺りからちょっと複雑ですが
基本的な考え方は「平面」の話と同様ですね。
線形空間 Vector Space
|| ベクトルを問題なく使える保証
「線型空間」「ベクトル空間」とも呼ばれます。
\begin{array}{cccccc} \displaystyle v,u,w&∈&V &&V \,\, \mathrm{is} \,\, \mathrm{Set \,\, of \,\, Vector} \\ \\ a,b&∈&S &&S \,\, \mathrm{is} \,\, \mathrm{Scalar \,\, Field} \end{array}
\begin{array}{cccccccc} \displaystyle (v+u)+w&=&v+(u+w) &&\mathrm{Associative} \\ \\ v+u&=&u+v &&\mathrm{Commutative} \\ \\ \\ v+\vec{0}&=&v&&\mathrm{Identity} \\ \\ v+(-v)&=&0 &&\mathrm{Inverse} \\ \\ \\ a\times (b\times v)&=&(a\times b)\times v&&\mathrm{Associative} \\ \\ 1\times v&=&v&&\mathrm{Identity} \\ \\ \\ a\times (v+u)&=&a\times v+a\times u&&\mathrm{Distributive} \\ \\ (a+b)\times v&=&a\times v+b\times v&&\mathrm{Distributive} \end{array}
\begin{array}{llllll} \displaystyle (V,+,\times) \,\, \mathrm{is} \,\, \mathrm{Vector \,\, Space} \,\, \mathrm{on} \,\, S \end{array}
ざっくりとした定義はこんな感じですが
とりあえずこれは一端スルーでOK
ベクトル Vector
|| スカラー値を並べたやつ
「スカラーを拡張したもの」のこと
\begin{array}{llllll} \displaystyle x,y &&→&&(1,2) \end{array}
「方向を持つ点」「組み合せ・セット」といった
そういう感覚を形式的に表現したものになります。
実践的には
\begin{array}{llllll} \displaystyle \mathrm{list} &=& [A,B,C,D,E,F] \end{array}
「配列・行列」の形式でよく使われます。
求められる性質
これは以下のような
「持っていて欲しい性質」から
\begin{array}{llllll} \displaystyle \vec{v}&=&(1,2) \\ \\ \vec{u}&=&(2,3) \end{array}
矛盾が出ないよう定義されています。
\begin{array}{cccccc} \vec{v}+\vec{u} &=& (3,5) && \mathrm{Addition} &\mathrm{Move} \\ \\ \displaystyle 2\vec{v} &=&(2,4) && \mathrm{Multiplication} & \mathrm{Length} \end{array}
こういった性質は定義なんですが
順番は要請が先なので気を付けましょう。
座標系の変換
この「ベクトル」という概念を使うと
異なる2つの「座標系」があった時
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \textcolor{gray}{1,3} & 2,3 \\ \\ \displaystyle 1,2 & \textcolor{gray}{2,2} \end{array} &&\to&& \begin{array}{llllll} \displaystyle \textcolor{gray}{0,1} & 1,1 \\ \\ 0,0 & \textcolor{gray}{1,0} \end{array} &&-(1,2) \\ \\ \\ \begin{array}{llllll} \textcolor{gray}{0,\displaystyle\frac{1}{2}} & \displaystyle\frac{1}{2},\frac{1}{2} \\ \\ \displaystyle 0,0 & \displaystyle\textcolor{gray}{\frac{1}{2},0} \end{array} &&\to&& \begin{array}{llllll} \displaystyle \textcolor{gray}{0,1} & 1,1 \\ \\ 0,0 & \textcolor{gray}{1,0} \end{array}&&\times 2 \end{array}
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \textcolor{gray}{0,\sin 45°} & \displaystyle\cos 45°,\sin 45° \\ \\ \displaystyle 0,0 & \textcolor{gray}{\cos 45°,0} \end{array} &&\to&& \begin{array}{llllll} \textcolor{gray}{0,\sin 60°} & \displaystyle\cos 60°,\sin 60° \\ \\ \displaystyle 0,0 & \textcolor{gray}{\cos 60°,0} \end{array} \end{array}
「平行移動」「伸縮」「回転」
こういったことが理解しやすくなります。
ノルム Norm
|| 距離とか長さを拡張した概念
「ベクトル」の『長さ』を意味するもの
\begin{array}{llllll} \displaystyle v_2&=&(x,y) \\ \\ v_3&=&(x,y,z) \end{array}
\begin{array}{llllll} \displaystyle ||v_2||_2&=&\displaystyle\sqrt{x^2+y^2} \\ \\ \displaystyle ||v_3||_2&=&\displaystyle\sqrt{x^2+y^2+z^2} \end{array}
代表的なこれらは
「ユークリッドノルム」と呼ばれるもので
\begin{array}{llllll} \displaystyle ||v_3||_2&=&\displaystyle \left( x^2+y^2+z^2 \right)^{\frac{1}{2}} \\ \\ \displaystyle ||v_3||_p&=&\displaystyle \left( x^p+y^p+z^p \right)^{\frac{1}{p}} \end{array}
更に一般化されたものは
こんな感じの記号で表現されます。
ただまあ使うのはほぼ「 2 -ノルム」で
\begin{array}{llllll} \displaystyle ||v||_2&≒&||v|| \end{array}
「ノルム」って言ったら
だいたい「 2 -ノルム」のことを指します。
内積 Inner Product
|| ベクトルの掛け算的な操作
「異なるベクトル」のノルムを求める感じ。
\begin{array}{llllll} \displaystyle v&=&(a,b,c) \\ \\ q&=&(x,y,z) \end{array}
\begin{array}{ccc} v \cdot q &=& \displaystyle ax+by+cz \\ \\ \langle v,q \rangle&=& \displaystyle ax+by+cz \end{array}
「方向を合わせて掛ける」感じの操作とも言えます。
\begin{array}{ccc} \displaystyle v \cdot u &=&||v|| \, ||u|| \, \cos θ \\ \\ \langle v,v \rangle &=&||v|| \, ||v|| \, \cos 0 &=&||v||^2\end{array}
これの歴史はわりとぐちゃぐちゃなので
発生起源やらなんやらはよく分かりません。
(第一人者はハミルトン・テイト・グラスマン)
内積の感覚
これは以下の感覚を定式化したもので
(「線型」なんて呼ばれる感覚)
\begin{array}{llllll} \displaystyle ax+by &→&(a,b)(x,y) \\ \\ ax+by+cz &→&(a,b,c)(x,y,z) \end{array}
\begin{array}{cccc} \displaystyle a_0 x^0 + a_1 x^1 + a_2 x^2 + \cdots + a_n x^n &=&0 \\ \\ x_1 p_1 + x_2 p_2 + x_3 p_3 + \cdots + x_np_n &=&E(X) \end{array}
基本的にそれ以上の意味を持ちません。
良い感じのツールという側面が強いです。
四元数 Quaternion
物理学における「仕事」に始まり
「ベクトル」の基盤と言える概念は
\begin{array}{llllll} \displaystyle q&=&a_0+a_1i+a_2j+a_3k \end{array}
\begin{array}{ccc} \displaystyle i^2&=& j^2&=& k^2&=& ijk&=&-1 \end{array}
\begin{array}{ccrrrrr} \displaystyle &&\times i&\times j&\times k \\ \\ i&& -1 & k & -j \\ \\ j&& -k & -1 & i \\ \\ k&& j & -i & -1 \end{array}
\begin{array}{ccr} \displaystyle 〇×&=&△ \\ \\ ×〇&=&-△ \end{array}
『独立した回転』を可能にする
「四元数 q 」と呼ばれてるものになります。
\begin{array}{llllll} \displaystyle \overbrace{a_0}^{\mathrm{Scalar}}+\underbrace{a_1i+a_2j+a_3k}_{\mathrm{Vector}} \end{array}
\begin{array}{llllll} \displaystyle a_1i+a_2j+a_3k &⇆& (a_1,a_2,a_3) \end{array}
数式としてはこんな感じで
(虚数のみではないため成分同士の関係を作れる)
\begin{array}{llllll} vu&=& \displaystyle (a_1i+a_2j+a_3k)(b_1i+b_2j+b_3k) \end{array}
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle a_1ib_1i+a_1ib_2j+a_1ib_3k \\ \\ a_2jb_1i+a_2jb_2j+a_2jb_3k \\ \\ a_3kb_1i+a_3kb_2j+a_3kb_3k \end{array} &=&\displaystyle \begin{array}{r} \displaystyle -a_1b_1+a_1b_2ij+a_1b_3ik \\ \\ a_2b_1ji-a_2b_2+a_2b_3jk \\ \\ a_3b_1ki+a_3b_2kj-a_3b_3 \end{array} \end{array}
\begin{array}{r} \displaystyle \textcolor{pink}{-a_1b_1}+a_1b_2\textcolor{steelblue}{k}-a_1b_3\textcolor{mediumaquamarine}{j} \\ \\ -a_2b_1\textcolor{steelblue}{k}\textcolor{pink}{-a_2b_2}+a_2b_3\textcolor{greenyellow}{i} \\ \\ a_3b_1\textcolor{mediumaquamarine}{j}-a_3b_2\textcolor{greenyellow}{i}\textcolor{pink}{-a_3b_3} \end{array}
\begin{array}{r} \displaystyle -(a_1b_1+a_2b_2+a_3b_3) \\ \\ (a_2b_3-a_3b_2)\textcolor{greenyellow}{i} \\ \\ (a_3b_1-a_1b_3)\textcolor{mediumaquamarine}{j} \\ \\ (a_1b_2-a_2b_1)\textcolor{steelblue}{k} \end{array}
ややこしいですが
「スカラー」部分と『その他』の部分から
\begin{array}{cccccc} \displaystyle a_1b_1+a_2b_2+a_3b_3 &&\mathrm{Inner} && \mathrm{Scalar} \\ \\ \displaystyle \left( \begin{array}{llllll} \displaystyle a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{array} \right)&&\mathrm{Outer} && \mathrm{Vector} \end{array}
結果的に
『ベクトル計算のスカラー部分』として
「内積」はこのような形で定義されました。
まとめると
つまり「内積」という操作は
\begin{array}{llllll} \displaystyle v\cdot u&=&a_1b_1+a_2b_2+a_3b_3 \end{array}
「ベクトル同士の掛け算」による
『スカラー値の抽出』を意味する操作だと言えます。
(四元数の定義が成分同士の関係を意味している)
行列 Matrix
|| ベクトルを拡張したやつ
「ベクトル」の「ベクトル」みたいな感じ
\begin{array}{ccccr} ax+by &&→&& \displaystyle \left( \begin{array}{llllll} \displaystyle a&b \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right) \\ \\ \displaystyle \left( \begin{array}{llllll} \displaystyle ax+by \\ cx+dy \end{array} \right)&&→&& \displaystyle \left( \begin{array}{llllll} \displaystyle a&b \\ c&d \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle ax+by&av+bu \\ cx+dy&cv+du \end{array} \right)&&→&& \displaystyle \left( \begin{array}{llllll} \displaystyle a&b \\ c&d \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x & v \\ y & u \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle \vec{a_1} \\ \vec{a_2} \end{array} \right)&=&\displaystyle \left( \begin{array}{llllll} \displaystyle a_{11}&a_{12} \\ a_{21} & a_{22} \end{array} \right) \end{array}
「連立方程式」とか
\begin{array}{rrr} \displaystyle \left( \begin{array}{llllll} \displaystyle 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \\ z \end{array} \right) &=&\displaystyle \left( \begin{array}{llllll} \displaystyle a \\ b \\ c \end{array} \right) \\ \\ \\ \displaystyle A^{-1}A\left( \begin{array}{llllll} \displaystyle x \\ y \\ z \end{array} \right) &=&\displaystyle A^{-1}\left( \begin{array}{llllll} \displaystyle c_1 \\ c_2 \\ c_3 \end{array} \right) \end{array}
「配列(ベクトル)の一括処理」
「点座標の一括処理」なんかでよく見ます。
\begin{array}{llllll} F(\mathrm{Data}_{\mathrm{matrix}}) &=& \displaystyle \left( \begin{array}{cccc} \displaystyle F(\mathrm{Data}_{\mathrm{vector}}) \\ \\ F(\mathrm{Data}_{\mathrm{vector}}) \\ \\ F(\mathrm{Data}_{\mathrm{vector}}) \\ \\ \vdots \end{array} \right) \end{array}
「画像の処理」とかが実感しやすいかもしれません。
身近な活用事例
こいつは一見するとよくわからんですが
実は身近なものにわりと使われていて
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} [255,0,0]&[0,255,0]&[0,0,255] \\ \\ [255,255,0]&[0,255,255] & [255,0,255] \\ \\ [0,0,0]&[127,127,127]&[255,255,255] \end{array} \right) \end{array}
例えば「画像のRGB」なんかをまとめて
「平行移動・伸縮・回転」なんかの
一括処理を行う場合とかで使われてます。
単位行列 Identity Matrix
「行列」の「かけ算的な操作」
(正方行列の話になります)
\begin{array}{rclcc} IA&=&AI&=&A \\ \\ \displaystyle EA&=&AE&=&A \\ \\ \hat{1}A&=& A\hat{1}&=&A \end{array}
\begin{array}{llllll} \displaystyle I_2&=&\displaystyle \left( \begin{array}{ccc} \displaystyle 1&0 \\ 0&1 \end{array} \right) \\ \\ \mathrm{diag}(1,1)&=&\displaystyle \left( \begin{array}{ccc} \displaystyle 1&0 \\ 0&1 \end{array} \right) \end{array}
これによって
「変化を起こさない行列」のことを
「単位行列」と言って
\begin{array}{llllll} \displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right)\displaystyle \left( \begin{array}{ccc} \displaystyle 1&0 \\ 0&1 \end{array} \right)&=&\displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right) \end{array}
具体的にはこういうやつが単位行列になります。
逆行列 Inverse Matrix
ある行列を「単位行列にする行列」のこと。
(掛け算で言うところの逆数みたいなやつ)
\begin{array}{llllll} \displaystyle AA^{-1}&=&I \end{array}
\begin{array}{llllll} \displaystyle A^{-1} &=& \displaystyle \frac{1}{\mathrm{det}(A)}\left( \begin{array}{ccc} \displaystyle d&-b \\ -c&a \end{array} \right) \end{array}
導出は力技です。
\begin{array}{llllll} \displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right)A^{-1} &=& \displaystyle \left( \begin{array}{ccc} \displaystyle 1&0 \\ 0&1 \end{array} \right) \end{array}
これから得られる連立方程式を解くと
\begin{array}{llllll} \displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right)\left( \begin{array}{ccc} \displaystyle x_{11}&x_{12} \\ x_{21}&x_{22} \end{array} \right) &=& \displaystyle \left( \begin{array}{ccc} \displaystyle ax_{11}+bx_{21}&ax_{12}+bx_{22} \\ cx_{11}+dx_{21}&cx_{12}+dx_{22} \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle \left\{ \begin{array}{llllll} \displaystyle ax_{11}+bx_{21}&=&1 \\ cx_{11}+dx_{21}&=&0 \end{array} \right. &&\to&& \displaystyle \left\{ \begin{array}{llllll} \displaystyle acx_{11}+bcx_{21}&=&c \\ acx_{11}+adx_{21}&=&0 \end{array} \right. \\ \\ \\ \displaystyle \left\{ \begin{array}{llllll} \displaystyle ax_{12}+bx_{22}&=&0 \\ cx_{12}+dx_{22}&=&1 \end{array} \right. &&\to&& \displaystyle \left\{ \begin{array}{llllll} \displaystyle acx_{12}+bcx_{22}&=&0 \\ acx_{12}+adx_{22}&=&a \end{array} \right. \end{array}
\begin{array}{llllll} (ad-bc)x_{21}&=&-c &&\to&&cx_{11}+dx_{21}&=&0 \\ \\ (ad-bc)x_{22}&=&a &&\to&& ax_{12}+bx_{22}&=&0 \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{ccc} \displaystyle x_{11}&x_{12} \\ x_{21}&x_{22} \end{array} \right) &=&\displaystyle \frac{1}{ad-bc}\left( \begin{array}{ccc} \displaystyle d&-b \\ -c&a \end{array} \right) \end{array}
\begin{array}{ccccc} \displaystyle A^{-1}A&=&I &&? \\ \\ A^{-1}I&=&A^{-1} &&〇 \\ \\ A^{-1}AA^{-1}&=&A^{-1} &&〇 \\ \\ (A^{-1}A)A^{-1}&=&A^{-1} &&〇 \end{array}
\begin{array}{llllll} \displaystyle AA^{-1}&=&I&=&A^{-1}A \end{array}
この結果に行き着きます。
またこれに伴い
\begin{array}{cccccc} \displaystyle ad-bc&=& 0 &&\mathrm{No} \\ \\ ad-bc&≠&0 && \mathrm{Exist} \end{array}
この値から
「逆行列の存在」を判定できるようになります。
線形写像 Linear Mapping
|| 点をどこにでも移動させることができる
「点を動かす」ことになる「行列」の名前
\begin{array}{llllll} \displaystyle A \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right)&=&\left( \begin{array}{llllll} \displaystyle x_A \\ y_A \end{array} \right) \end{array}
「線型変換」「一次変換」とも呼ばれます。
あまり直感的には理解しにくいですが
「連立方程式」の感覚から分かる通り
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle a&b \\ c&d \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right) &=&\displaystyle \left( \begin{array}{llllll} \displaystyle α \\ β \end{array} \right) \end{array}
『連立方程式の係数』をまとめた「行列」
この中身 a,b,c,d を好きに書き換えれば
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right) &→&\displaystyle \left( \begin{array}{llllll} \displaystyle α \\ β \end{array} \right) \end{array}
『あらゆる場所』に点を移動させることができる
というのはなんとなく実感できると思います。
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle a&b \\ c&d \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle 0 \\ 0 \end{array} \right) &=&\displaystyle \left( \begin{array}{llllll} \displaystyle 0 \\ 0 \end{array} \right) \end{array}
同様に
これが「原点 (0,0) を動かさない」
ということも分かるかと。
伸縮
分かりやすい話
\begin{array}{llllll} 2I &=& \displaystyle \left( \begin{array}{llllll} \displaystyle 2&0 \\ 0&2 \end{array} \right) \end{array}
例えば「定数倍した単位行列」は
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle 2&0 \\ 0&2 \end{array} \right) \displaystyle \left( \begin{array}{llllll} \displaystyle x \\ y \end{array} \right) &=&\displaystyle \left( \begin{array}{llllll} \displaystyle 2x \\ 2y \end{array} \right) \end{array}
「伸縮させる線型写像」です。
これは直感的に分かると思います。
回転行列 Rotate
「極座標系」の感覚から
\begin{array}{lcrlllll} \displaystyle x&=&r\cos α \\ y&=&r\sin α \end{array}
\begin{array}{lcc} \displaystyle R_{θ} \displaystyle \left( \begin{array}{r} \displaystyle r\cos α \\ r\sin α \end{array} \right) &=&\displaystyle \left( \begin{array}{r} \displaystyle r\cos (θ+α) \\ r\sin (θ+α) \end{array} \right) \end{array}
「三角関数の加法定理」より
\begin{array}{rr} \displaystyle \cos (θ+α)&=&\cos θ\cos α - \sin θ \sin α \\ \sin (θ+α)&=&\sinθ \cos α + \cosθ \sin α \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{r} \displaystyle \cos (θ+α) \\ \sin (θ+α) \end{array} \right) &=& \displaystyle \left( \begin{array}{rr} \displaystyle \cos θ & -\sin θ \\ \sin θ & \cos θ \end{array} \right) \left( \begin{array}{rr} \displaystyle \cos α \\ \sin α \end{array} \right) \end{array}
以下のような
\begin{array}{llllll} \displaystyle R_θ&=&\displaystyle \left( \begin{array}{rr} \displaystyle \cos θ & -\sin θ \\ \sin θ & \cos θ \end{array} \right) \end{array}
『その場から θ 回転させる』ことになる
「線型写像」を得ることができます。
ちなみに
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle 1&0 \\ 0&1 \end{array} \right) &=&\displaystyle \left( \begin{array}{rr} \displaystyle \cos 0 & -\sin 0 \\ \sin 0 & \cos 0 \end{array} \right) \end{array}
「回転行列」の視点から見ると
「単位行列」は「回転させない操作」になります。
任意の位置に移動させられる
以上の話から分かると思いますが
\begin{array}{llllll} \displaystyle tIR_θ&=&\displaystyle \left( \begin{array}{llllll} \displaystyle t&0 \\ 0&t \end{array} \right)\left( \begin{array}{rr} \displaystyle \cos θ & -\sin θ \\ \sin θ & \cos θ \end{array} \right) \end{array}
「極座標系」を知っていれば分かる通り
この2つの「線形写像」があれば
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle t&0 \\ 0&t \end{array} \right) \left( \begin{array}{rr} \displaystyle \cos θ & -\sin θ \\ \sin θ & \cos θ \end{array} \right) \left( \begin{array}{rr} \displaystyle r\cos α \\ r\sin α \end{array} \right) &=& \displaystyle \left( \begin{array}{r} \displaystyle tr\cos (θ+α) \\ tr\sin (θ+α) \end{array} \right) \end{array}
「原点以外の点」であれば
あらゆる座標に移動させることが可能になります。
これは『 (1,0) に変換できる』という事実から
\begin{array}{llllll} \displaystyle \frac{1}{r} \left( \begin{array}{rr} \displaystyle \cos (-α) & -\sin (-α) \\ \sin (-α) & \cos (-α) \end{array} \right) \left( \begin{array}{rr} \displaystyle r\cos α \\ r\sin α \end{array} \right) &=&\displaystyle \left( \begin{array}{rr} \displaystyle \cos 0 \\ \sin 0 \end{array} \right) \end{array}
直感的に理解できるかと。
行列式 Determinant
|| 正方行列で定義できる意味のある量
「逆行列」から導かれるやつ
\begin{array}{lcc} A&=&\displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right) \\ \\ A^{-1} &=& \displaystyle \frac{1}{\mathrm{det}(A)}\left( \begin{array}{ccc} \displaystyle d&-b \\ -c&a \end{array} \right) \end{array}
\begin{array}{ccc} \displaystyle \mathrm{det}(A)&=&\displaystyle \left| \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right| \\ \\ &=&ad-bc \end{array}
この時点じゃこれだけの意味しか持ちません。
行列式と面積
「面積 1 の正方形」を
『線型写像(行列)で拡大する』
そういった操作を考えた時の
\begin{array}{llllll} \displaystyle I&=&\displaystyle \left( \begin{array}{ccc} \displaystyle 1&0 \\ 0&1 \end{array} \right) \end{array}
「正方形」を変形する
「線形写像としての行列 A 」
その演算結果から作られる「平行四辺形」
\begin{array}{llllll} A&=&\displaystyle \left( \begin{array}{ccc} \displaystyle a&b \\ c&d \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle A \left( \begin{array}{ccc} \displaystyle 1 \\ 0 \end{array} \right)&=&\displaystyle \left( \begin{array}{ccc} \displaystyle a \\ c \end{array} \right) \\ \\ \displaystyle A \left( \begin{array}{ccc} \displaystyle 0 \\ 1 \end{array} \right)&=&\displaystyle \left( \begin{array}{ccc} \displaystyle b \\ d \end{array} \right) \end{array}
(正方形を成す単位ベクトル (1,0),(0,1) の移動)
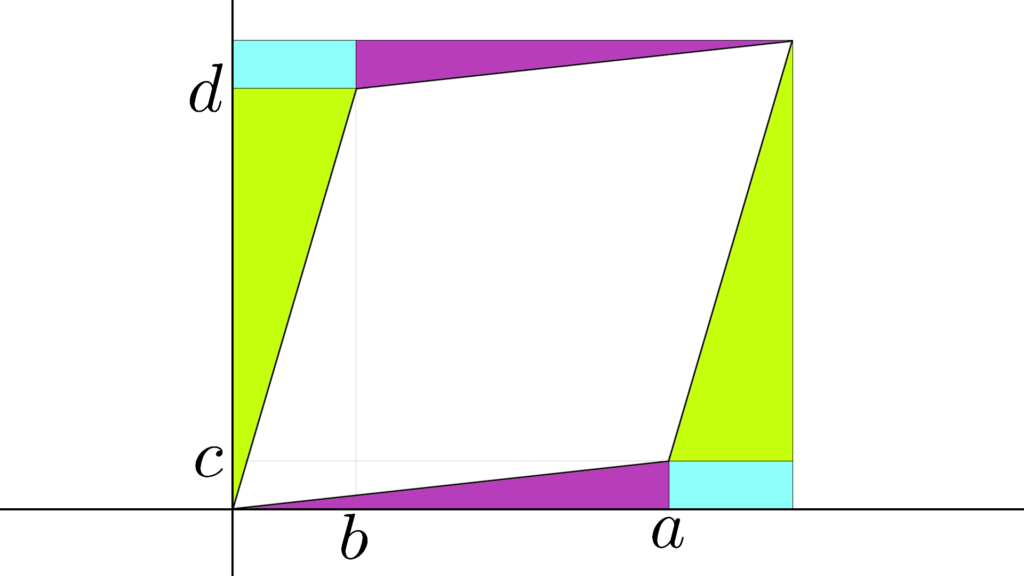
\begin{array}{llllll} \displaystyle (a+b)(c+d)&=&\textcolor{darkmagenta}{ac}+ad+\textcolor{aqua}{bc}+\textcolor{greenyellow}{bd} \end{array}
\begin{array}{rcc} \displaystyle \textcolor{aqua}{bc}×2 \\ \\ \displaystyle \frac{1}{2} \textcolor{darkmagenta}{ac}×2 \\ \\ \displaystyle \frac{1}{2} \textcolor{greenyellow}{db}×2 \end{array}
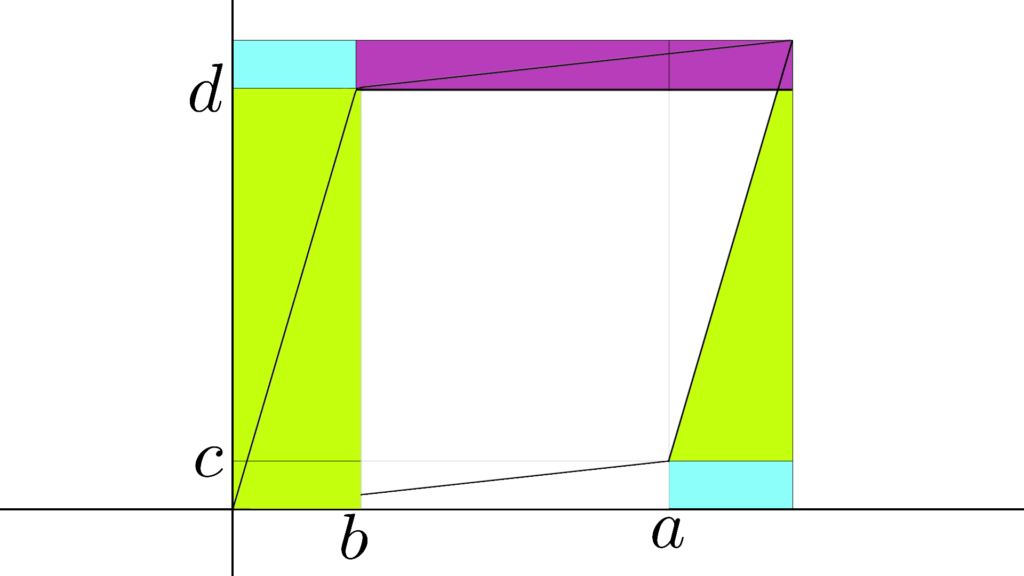
\begin{array}{llllll} \displaystyle (a+b)(c+d) - \left( 2\textcolor{aqua}{bc}+\frac{1}{2} 2\textcolor{darkmagenta}{ac} + \frac{1}{2} 2\textcolor{greenyellow}{db} \right) &=&ad-bc \\ \\ &=&\mathrm{det}(A) \end{array}
この面積もまた \mathrm{det}(A) になります。
関数行列 Jacobian Matrix
|| ある関数の各変数の方向微分を並べた行列
『全微分の中身』を集めた「行列」のこと
\begin{array}{llllll} \displaystyle |J|&=& \displaystyle\frac{\partial (x,y)}{\partial (r,θ)} &=&\displaystyle\frac{dxdy}{drdθ} \\ \\ && \displaystyle\frac{\partial (x,y)}{\partial (r,θ)} &=&\displaystyle\left| \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right| \end{array}
\begin{array}{llllll} \displaystyle J&=&\displaystyle\left( \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right) \end{array}
「ヤコビ行列」「ヤコビアン」とも言われます。
\begin{array}{ccc} \displaystyle x&=&(x_1,x_2,x_3,\cdots,x_i) \\ \\ f(x)&=&\displaystyle \left( \begin{array}{c} \displaystyle f_1(x_1,x_2,x_3,\cdots,x_i) \\ \\ f_2(x_1,x_2,x_3,\cdots,x_i) \\ \\ \vdots \\ \\ f_n(x_1,x_2,x_3,\cdots,x_i) \end{array} \right) \end{array}
\begin{array}{cccccccc} \displaystyle \displaystyle J_f&=&\displaystyle\left( \begin{array}{cccccccccccc} \displaystyle \frac{\partial f_1}{\partial x_1} & \displaystyle \frac{\partial f_1}{\partial x_2} &\cdots &\displaystyle\frac{\partial f_1}{\partial x_i} \\ \\ \vdots &\vdots &&\vdots \\ \\ \displaystyle\frac{\partial f_n}{\partial x_1} &\displaystyle\frac{\partial f_n}{\partial x_2} &\cdots &\displaystyle\frac{\partial f_n}{\partial x_i} \end{array} \right) \end{array}
一般化するとこんな感じなんですが
これじゃなんも分からんですね。
ふわっとした意味
これはいったいなんなのか
簡単に説明するのは難しいですが
\begin{array}{cccccccc} \displaystyle \displaystyle J_f&=&\displaystyle\left( \begin{array}{cccccccccccc} \displaystyle \frac{\partial f_1}{\partial x_1} & \displaystyle \frac{\partial f_1}{\partial x_2} &\cdots &\displaystyle\frac{\partial f_1}{\partial x_i} \\ \\ \vdots &\vdots &&\vdots \\ \\ \displaystyle\frac{\partial f_n}{\partial x_1} &\displaystyle\frac{\partial f_n}{\partial x_2} &\cdots &\displaystyle\frac{\partial f_n}{\partial x_i} \end{array} \right) \end{array}
なんとなく
「まとめたもの」であることは分かると思います。
というのも
例えば「多変数関数の全微分」を行う場合
\begin{array}{llllll} \displaystyle dz&=&df(x,y) \\ \\ &=&f(x+dx,y+dy)-f(x,y) \\ \\ &=&\displaystyle\frac{\partial f}{\partial x}dx +\frac{\partial f}{\partial y}dy \end{array}
「座標 z 」の計算から
「 dz の微小変化」については
このように書かれるわけですが
これを分解して並べると
\begin{array}{llllll} dz&=& \displaystyle \left( \begin{array}{llllll} \displaystyle \frac{\partial f}{\partial x} &\displaystyle \frac{\partial f}{\partial y} \end{array} \right) \left(\begin{array}{llllll} \displaystyle dx \\ dy \end{array}\right) \end{array}
「内積」の形を考えれば
こんな感じになりますよね。
で、他の x,y を変数に持つ関数 g(x,y) を考えると
\begin{array}{llllll} dz &=& \displaystyle \left( \begin{array}{llllll} \displaystyle \frac{\partial g}{\partial x} &\displaystyle \frac{\partial g}{\partial y} \end{array} \right) \left(\begin{array}{llllll} \displaystyle dx \\ dy \end{array}\right) \end{array}
これもこうで
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle\frac{\partial f}{\partial x} &\displaystyle \frac{\partial f}{\partial y} \\ \\ \displaystyle \frac{\partial g}{\partial x} &\displaystyle \frac{\partial g}{\partial y} \end{array} \right) \left(\begin{array}{llllll} \displaystyle dx \\ dy \end{array}\right) \end{array}
これらは「行列」の定義から
このように書くことができます。
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle\frac{\partial f}{\partial x}dx + \displaystyle \frac{\partial f}{\partial y}dy \\ \\ \displaystyle \frac{\partial g}{\partial x}dx + \displaystyle \frac{\partial g}{\partial y}dy \end{array} \right) \end{array}
これは計算するとこうなりますから。
とまあ要はそんな感じで
\begin{array}{llllll} \displaystyle dz&=&\displaystyle \left( \begin{array}{llllll} \displaystyle\frac{\partial f}{\partial x}dx + \displaystyle \frac{\partial f}{\partial y}dy \\ \\ \displaystyle \frac{\partial g}{\partial x}dx + \displaystyle \frac{\partial g}{\partial y}dy \end{array} \right) \end{array}
「内積」で「全微分」を表現して拡張したもの
全ての偏微分の成分を綺麗に並べて整理したもの
\begin{array}{llllll} \displaystyle J&=&\displaystyle\left( \begin{array}{llllll} \displaystyle \frac{\partial f}{\partial x} &\displaystyle\frac{\partial f}{\partial y} \\ \\ \displaystyle\frac{\partial g}{\partial x} &\displaystyle\frac{\partial g}{\partial y} \end{array} \right) \end{array}
この辺りが
「関数行列」の持つ意味になります。
使用される例
これは主に「変数の変換」で用いられます。
\begin{array}{llllll} \displaystyle x,y &&→&& r,θ \end{array}
具体的には
「極座標系」への変換を行う時の
「微小面積・体積」の比率を求める時に
\begin{array}{llllll} \displaystyle dxdy &&→&& drdθ \end{array}
「行列式」から
「微小面積」を直接的に求めて
\begin{array}{llllll} \displaystyle dxdy&=&\displaystyle\left| \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right|drdθ \end{array}
「座標系」間の変数の比率を求める、という感じで。
(この行列式もヤコビアンと呼ばれます)
微小面積の導出
↑ の説明だけじゃ分からないと思うので
ちょっとこの辺りを補足しておくと
\begin{array}{llllll} \displaystyle dxdy \end{array}
まずやってることなんですが
これは「面積の計算」です。
\begin{array}{llllll} 0,dy&&dx,dy \\ \\ \displaystyle 0,0 && 0,dx \end{array}
これを「図形的に」見て
そのまま直接的に求める。
\begin{array}{llllll} 底辺×高さ &&→&& \displaystyle dxdy \end{array}
やってることはただそれだけで
\begin{array}{llllll} \displaystyle dx&=& \displaystyle \frac{\partial x}{\partial r}dr +\displaystyle\frac{\partial x}{\partial θ}dθ \\ \\ dy&=&\displaystyle\frac{\partial y}{\partial r}dr +\displaystyle\frac{\partial y}{\partial θ}dθ \end{array}
後はこの「全微分」の関係から
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right) \displaystyle\left( \begin{array}{llllll} dr \\ dθ \end{array} \right) \end{array}
「ヤコビアン」を「線型写像」とみなして
\begin{array}{llllll} \begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right) \displaystyle\left( \begin{array}{llllll} dr \\ dθ \end{array} \right) \end{array}&=&\displaystyle\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} 1&0 \\ 0&1 \end{array} \right) \displaystyle\left( \begin{array}{llllll} dx \\ dy \end{array} \right) \end{array} \end{array}
これらの面積を考えると
\begin{array}{llllll}\displaystyle\left| \begin{array}{llllll} \displaystyle \frac{\partial x}{\partial r} &\displaystyle\frac{\partial x}{\partial θ} \\ \\ \displaystyle\frac{\partial y}{\partial r} &\displaystyle\frac{\partial y}{\partial θ} \end{array} \right| drdθ&=&\displaystyle\left| \begin{array}{llllll} 1&0 \\ 0&1 \end{array} \right| dxdy \end{array}
↑ の等式からそのまま値を取り出せば
結果としてこのような結論が得られます。
