|| 微分の基本的な形についてまとめてみた
導出まできちんと確認してます。
スポンサーリンク
\begin{array}{rllllll} (c)^{\prime}&=&0 \\ \\ \displaystyle \left( x^α \right)^{\prime}&=&αx^{α-1} \\ \\ \\ \displaystyle \left( \sin x \right)^{\prime}&=&\cos x \\ \\ \displaystyle \left( \cos x \right)^{\prime}&=&-\sin x \\ \\ (\tan x)^{\prime}&=&\displaystyle \frac{1}{\cos^2 x} \\ \\ \displaystyle \left( \frac{1}{\tan x} \right)^{\prime}&=&\displaystyle -\frac{1}{\sin^2 x} \\ \\ \\ \displaystyle \left( e^x \right)^{\prime}&=&e^x \\ \\ \displaystyle \left( a^x \right)^{\prime}&=&a^x\log a \\ \\ \displaystyle \left( \log x \right)^{\prime}&=&\displaystyle\frac{1}{x} \end{array}
この記事では
上記の微分について解説していきます。
目次
定数「変化しないから 0 」
冪関数「 x^n の微分」
三角関数「行ったり来たり」
指数関数「ほぼ変化無し」
対数関数「よく分からない結果になる」
定数関数 c
当たり前すぎる話ですけど
これはめちゃくちゃ重要な結果になります。
\begin{array}{rllllll} \displaystyle f(x)&=&c \\ \\ \displaystyle\frac{d}{dx}f(x)&=&0 \end{array}
\begin{array}{llllll} \displaystyle \Bigl(f(x) \Bigr)^{\prime}&=&\displaystyle\lim_{h\to 0}\frac{f(x+h)-f(x)}{(x+h)-x} \\ \\ \\ &=&\displaystyle\lim_{h\to 0}\frac{c-c}{(x+h)-x} \\ \\ &=&\displaystyle\lim_{h\to 0}\frac{0}{(x+h)-x} \\ \\ \\ &=&\displaystyle\lim_{h\to 0} 0 \\ \\ &=&0 \end{array}
『微分すると定数を消せる』
これはいたるところで使われていて
微分の操作の中でも基本中の基本
\begin{array}{llllll} \displaystyle \frac{d}{dx}c&=&0 \end{array}
ほぼ定義と言って良いものになります。
冪関数 x^α
これは式変形で求められます。
「二項定理」が必要ですが他は簡単
\begin{array}{llllll} \displaystyle \left( x^n \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{(x+h)^n-x^n}{(x+h)-x} \end{array}
\begin{array}{llllll} \displaystyle (x+h)^n&=&\displaystyle(x+h)(x+h)(x+h)\cdots(x+h) \\ \\ &=&{}_n \mathrm{C}_0x^nh^0 + {}_n \mathrm{C}_1x^{n-1}h^1 +\cdots+{}_n \mathrm{C}_n x^0h^n \end{array}
\begin{array}{llllll} \displaystyle \frac{(x+h)^n-x^n}{(x+h)-x}&=&\displaystyle \frac{{}_n \mathrm{C}_0x^nh^0 + {}_n \mathrm{C}_1x^{n-1}h^1 +\cdots+{}_n \mathrm{C}_n x^0h^n-x^n}{h} \\ \\ &=&\displaystyle \frac{x^n + {}_n \mathrm{C}_1x^{n-1}h^1 +\cdots+{}_n \mathrm{C}_n x^0h^n-x^n}{h} \\ \\ \\ &=&\displaystyle \frac{ {}_n \mathrm{C}_1x^{n-1}h^1 +{}_n \mathrm{C}_2x^{n-2}h^2+\cdots+{}_n \mathrm{C}_n x^0h^n}{h} \\ \\ &=&\displaystyle {}_n \mathrm{C}_1x^{n-1}h^{1-1} +{}_n \mathrm{C}_2x^{n-2}h^{2-1}+\cdots+{}_n \mathrm{C}_n x^0h^{n-1} \\ \\ \\ &=&\displaystyle nx^{n-1} +{}_n \mathrm{C}_2x^{n-2}h^{1}+\cdots+{}_n \mathrm{C}_n x^0h^{n-1} \end{array}
\begin{array}{llllll} \displaystyle \left( x^n \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{(x+h)^n-x^n}{(x+h)-x} \\ \\ &=&\displaystyle \lim_{h\to 0}\displaystyle nx^{n-1} +{}_n \mathrm{C}_2x^{n-2}h^{1}+\cdots+{}_n \mathrm{C}_n x^0h^{n-1} \\ \\ &=&nx^{n-1} \end{array}
展開がちょっと複雑ですけど
二項定理を理解していればすぐ分かると思います。
負の整数
負の整数でもいけます。
\begin{array}{llllll} \displaystyle \left( x^{-n} \right)^{\prime}&=&\displaystyle \left( \frac{1}{x^n} \right)^{\prime} \end{array}
\begin{array}{llllll} \displaystyle \left( \frac{1}{f(x)} \right)^{\prime}&=&\displaystyle -\frac{f^{\prime}(x)}{\left( f(x) \right)^2} \end{array}
「商の微分」がちょっとあれですが
\begin{array}{llllll} \displaystyle \displaystyle \left( \frac{1}{x^n} \right)^{\prime}&=&\displaystyle -\frac{\left( x^{n} \right)^{\prime}}{\left( x^n \right)^2} \\ \\ &=&\displaystyle -\frac{nx^{n-1}}{ x^{2n}} \\ \\ &=&\displaystyle -\frac{nx^{-1}}{ x^{n}} \\ \\ &=&\displaystyle -nx^{-n-1} \end{array}
まあどう見てもOK
ということは
n=0 は定数の微分として例外だとすると
\begin{array}{llllll} \displaystyle \displaystyle \left( x^n \right)^{\prime}&=&nx^{n-1} \end{array}
n は全ての整数でこうなると言えます。
n 以外でも行ける
↑ は n が整数の場合の話ですが
\begin{array}{llllll} \displaystyle \left( x^α \right)^{\prime}&=&αx^{α-1} \end{array}
これは x>0 の範囲では
全ての実数 α で成立します。
\begin{array}{rrrllll} \displaystyle y&=&x^α \\ \\ \log y&=&\log x^α \end{array}
これを証明するには
「対数微分法」というものを使うわけですが
\begin{array}{llrllll} \displaystyle \log y&=&\log x^α \\ \\ \log y&=&α\log x \end{array}
\begin{array}{llllll} \displaystyle \frac{d}{dx}\log x &=&\displaystyle \frac{1}{x} \\ \\ \displaystyle \frac{d}{dx}\log y &=&\displaystyle \frac{y^{\prime}}{y} \end{array}
\begin{array}{llllll} \displaystyle \frac{y^{\prime}}{y}&=&α\displaystyle \frac{1}{x} \\ \\ \displaystyle y^{\prime}&=&α\displaystyle \frac{y}{x} \\ \\ &=&α\displaystyle \frac{x^α}{x} \\ \\ &=&α\displaystyle x^{α-1} \end{array}
まあやることはただの式変形です。
ちょっとごちゃついてますし
対数関数の仕様で x>0 の範囲しか保証しませんけど
\begin{array}{llllll} \displaystyle \left( x^α \right)^{\prime}&=&αx^{α-1} \end{array}
x=0 で成立するのは明らかなので
x≥0 の範囲でなら
全ての実数 α でこれが成立します。
負の数
↑ は x の範囲を気にしてますけど
実はこれ、負の実数のパターンでもそこそこ行けます。
\begin{array}{llllll} \displaystyle \log y &&〇 \\ \\ \log -y &&× \end{array}
というのも
「負ではいけない」理由は
「対数が取れないから」なので
\begin{array}{llllll} \displaystyle \log |y| &=&\log |x^α| \end{array}
例えば「 x<0 で y<0 になる」パターンでも
「 y が虚数になる」パターンでも
正の値になるようにすれば
\begin{array}{llllll} \displaystyle \frac{-y^{\prime}}{-y}&=&α\displaystyle (-1)\frac{1}{-x} \\ \\ \displaystyle y^{\prime}&=&α\displaystyle \frac{y}{x} \\ \\ &=&α\displaystyle \frac{x^α}{x} \\ \\ &=&α\displaystyle x^{α-1} \end{array}
仮に y が負であったとしても
\begin{array}{llllll} \displaystyle \frac{\left( \sqrt{y\overline{y}} \right)^{\prime}}{\sqrt{y\overline{y}}}&=&α\displaystyle (-1)\frac{1}{-x} \end{array}
\begin{array}{llrllll} \displaystyle y&=&+x^α \\ \\ \overline{y}&=&-x^α \end{array}
\begin{array}{rrrllllll} \displaystyle y\overline{y}&=&\displaystyle -x^{2α} \\ \\ \displaystyle \sqrt{y\overline{y}}&=&\displaystyle \sqrt{-x^{2α}} \\ \\ &=&ix^{α} \end{array}
\begin{array}{llllll} \displaystyle \frac{\left( \sqrt{y\overline{y}} \right)^{\prime}}{\sqrt{y\overline{y}}}&=&α\displaystyle (-1)\frac{1}{-x} \\ \\ \displaystyle \frac{(ix^{α})^{\prime}}{ix^{α}}&=&α\displaystyle (-1)\frac{1}{-x} \\ \\ \displaystyle \frac{(x^{α})^{\prime}}{x^{α}}&=&α\displaystyle \frac{1}{x} \end{array}
虚数であったとしても
同様の結果を導くことができます。
\begin{array}{llllll} \displaystyle \frac{(x^α)^{\prime}}{x^α}&=&α\displaystyle \frac{1}{x}\end{array}
まあつまり y が+でも-でも虚数でも
必ずこのようになるので
\begin{array}{llllll} \displaystyle \left( x^α \right)^{\prime}&=&αx^{α-1} \end{array}
y が負あるいは虚数のパターンでは
x<0 でもまた成立すると言えます。
( α が無理数とかだとよく分からん)
有理数
有理数は全部大丈夫です。
ただそのまま求めるのは無理なので
\begin{array}{llllll} \displaystyle \left( x^{\frac{1}{n}} \right)^{\prime} \\ \\ \displaystyle \left( x^{\frac{m}{n}} \right)^{\prime} \end{array}
↓ の形が分かってることから
\begin{array}{llllll} \displaystyle \left( x^{n} \right)^{\prime}&=&nx^{n-1} \end{array}
これの逆関数を求めた上で
「逆関数の微分法」を用いることでこれを求めます。
\begin{array}{llllll} \displaystyle y&=&\displaystyle x^{\frac{1}{n}} \\ \\ \displaystyle y^n&=&\displaystyle \left( x^{\frac{1}{n}} \right)^n \\ \\ y^n&=&x \end{array}
\begin{array}{llllll} \displaystyle \frac{dy}{dx}&=&\displaystyle \frac{1}{\frac{dx}{dy}} \end{array}
\begin{array}{llllll} \displaystyle \frac{dx}{dy}&=&\displaystyle\left( y^n \right)^{\prime} \\ \\ &=&\displaystyle ny^{n-1}\end{array}
\begin{array}{llllll} \displaystyle y^{n-1}&=&\displaystyle \left( x^{\frac{1}{n}} \right)^{n-1} \\ \\ &=&\displaystyle \left( x^{\frac{1}{n}} \right)^{n}\displaystyle \left( x^{\frac{1}{n}} \right)^{-1} \\ \\ \\ &=&x^1x^{-\frac{1}{n}} \\ \\ &=&x^{ 1-\frac{1}{n}} \\ \\ &=&\displaystyle \frac{1}{x^{ \frac{1}{n}-1 }} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \frac{dy}{dx}&=&\left( x^{\frac{1}{n}} \right)^{\prime} \\ \\ &=&\displaystyle \frac{1}{ny^{n-1}} \\ \\ \\ &=&\displaystyle \frac{1}{n}x^{\frac{1}{n}-1} \end{array}
するとこう。
で、このパターンが分かったので
後は有理数全体に拡張するために
適当に 0 ではない整数 m を使うと
\begin{array}{llllll} \displaystyle y&=&x^{\frac{m}{n}} \\ \\ &=&\displaystyle \left( x^{\frac{1}{n}} \right)^{m} \end{array}
式はこのようになりますから
さっき求めたやつをひとまとめにしてやれば
\begin{array}{llllll} \displaystyle u&=&\left( x^{\frac{1}{n}} \right) \end{array}
\begin{array}{llllll} \displaystyle \frac{du}{dx}&=&\displaystyle\left( x^{\frac{1}{n}} \right)^{\prime} \\ \\ &=&\displaystyle \frac{1}{n}x^{\frac{1}{n}-1} \end{array}
後は「合成関数の微分」を用いれば
\begin{array}{llllll} \displaystyle \frac{dy}{dx}&=&\displaystyle \frac{dy}{du}\frac{du}{dx} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \left( x^{\frac{m}{n}} \right)^{\prime} &=& \left( u^m \right)^{\prime} \left( x^{\frac{1}{n}} \right)^{\prime} \\ \\ &=&\displaystyle mu^{m-1} \left( x^{\frac{1}{n}} \right)^{\prime} \\ \\ \\ &=&\displaystyle m\left( x^{\frac{1}{n}} \right)^{m-1}\frac{1}{n}x^{\frac{1}{n}-1} \\ \\ &=&\displaystyle\frac{m}{n}\left( x^{\frac{1}{n}} \right)^{m-1}x^{\frac{1}{n}-1} \end{array}
\begin{array}{llllll} \displaystyle \left( x^{\frac{1}{n}} \right)^{m-1}&=&x^{\frac{1}{n}}x^{\frac{1}{n}}\cdots x^{\frac{1}{n}} \\ \\ &=&\displaystyle x^{\frac{m-1}{n}} \end{array}
\begin{array}{llllll} \displaystyle \left( x^{\frac{1}{n}} \right)^{m-1}x^{\frac{1}{n}-1}&=&\displaystyle x^{\frac{m-1}{n}}x^{\frac{1}{n}-1} \\ \\ &=&x^{\frac{m-1}{n}+\frac{1}{n}-1 } \\ \\ &=&x^{\frac{m-1+1}{n}-1 } \\ \\ &=&x^{\frac{m}{n}-1 } \end{array}
\begin{array}{llllll} \displaystyle \left( x^{\frac{m}{n}} \right)^{\prime} &=&\displaystyle \frac{m}{n}x^{\frac{m}{n}-1} \end{array}
求めることができます。
以上
これで有理数全体でも大丈夫なことが分かりました。
三角関数 \sin x,\cos x,\tan x
\sin x と \cos x は
加法定理で計算すると楽に求められます。
\begin{array}{llrllll} \displaystyle \displaystyle \left( \sin x \right)^{\prime}&=&\cos x \\ \\ \displaystyle \left( \cos x \right)^{\prime}&=&-\sin x \end{array}
\tan x はちょっと後回し。
\begin{array}{clrllll} (\tan x)^{\prime}&=&\displaystyle \frac{1}{\cos^2 x} \\ \\ \displaystyle \left( \frac{1}{\tan x} \right)^{\prime}&=&\displaystyle -\frac{1}{\sin^2 x} \end{array}
\sin x,\cos x とは毛色が異なるので。
\cos x
図形や和積でも行けますが
\begin{array}{llllll} \displaystyle \cos (α+β) &=& \cos α \cos β - \sin α \sin β \\ \\ \displaystyle \cos (x+h) &=& \cos x \cos h - \sin x \sin h \end{array}
\begin{array}{llllll} \displaystyle \left(\cos x \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{\cos(x+h)-\cos x}{(x+h)-x} \\ \\ &=&\displaystyle \lim_{h\to 0}\frac{\cos x \cos h - \sin x \sin h-\cos x}{(x+h)-x} \\ \\ &=&\displaystyle \lim_{h\to 0}\frac{\cos x(\cos h - 1)-\sin x \sin h}{h} \\ \\ &=&\displaystyle \lim_{h\to 0}\frac{\cos x(\cos h - 1)}{h}-\frac{\sin x \sin h}{h} \\ \\ &=&\displaystyle \lim_{h\to 0}\cos x\frac{(\cos h - 1)}{h}-\sin x\frac{ \sin h}{h} \end{array}
\begin{array}{llllll} \displaystyle \lim_{x\to 0}\frac{ \sin x}{x} &=&1 \\ \\ \displaystyle \lim_{x\to 0}\frac{(\cos x - 1)}{x}&=&0 \end{array}
\begin{array}{llllll} \displaystyle \left(\cos x \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{\cos(x+h)-\cos x}{(x+h)-x} \\ \\ &=&\displaystyle \displaystyle \lim_{h\to 0}\cos x\frac{(\cos h - 1)}{h}-\sin x\frac{ \sin h}{h} \\ \\ &=&\cos x \times 0 -\sin x \times 1 \\ \\ &=& -\sin x \end{array}
加法定理が一番分かりやすいと思います。
\sin x
やることはほぼ \cos x の時と同じです。
\begin{array}{llllll} \displaystyle \sin (α+β) &=& \sin α \cos β + \cos α \sin β \\ \\ \displaystyle \sin (x+h) &=& \sin x \cos h + \cos x \sin h \end{array}
\begin{array}{llllll} \displaystyle \left(\sin x \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{\sin(x+h)-\sin x}{(x+h)-x} \\ \\ &=&\displaystyle\lim_{h\to 0}\frac{\sin x \cos h + \cos x \sin h-\sin x}{(x+h)-x} \\ \\ &=&\displaystyle\lim_{h\to 0}\frac{\sin x (\cos h-1) + \cos x \sin h}{(x+h)-x} \\ \\ \\ &=&\displaystyle \displaystyle \lim_{h\to 0}\sin x\frac{(\cos h - 1)}{h}+\cos x\frac{ \sin h}{h} \\ \\ &=&\sin x \times 0+\cos x \times 1 \end{array}
これも加法定理が一番分かりやすいと思います。
加法定理
本筋から逸れるので詳しくはやりません。
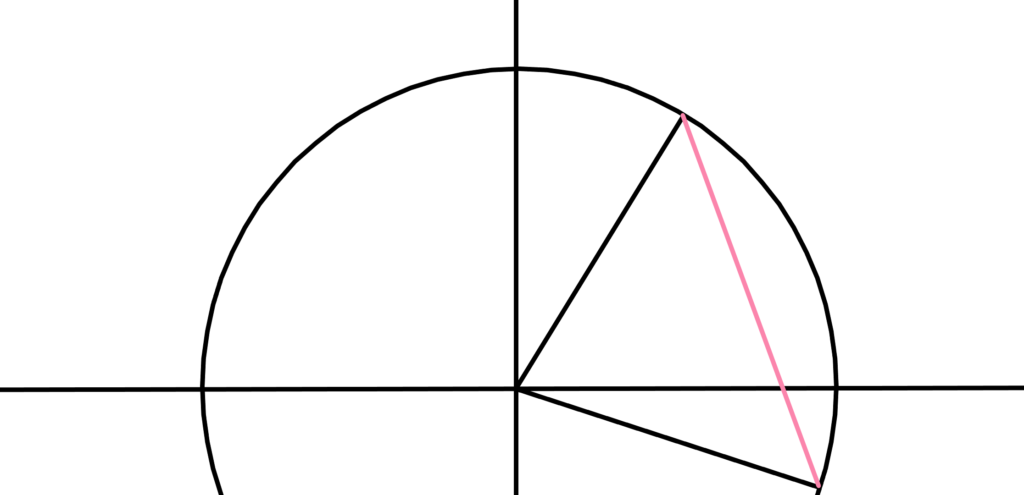
\begin{array}{ccllllll} \displaystyle A&B \\ \\ 1,0 &\cos(α+β),\sin(α+β) \\ \\ \\ A^{\prime}&B^{\prime} \\ \\ \cos(-α),\sin(-α)&\cos(β),\sin(β) \end{array}
図形全体を回転させてこの2点をとって
\begin{array}{llllll} \displaystyle AB&=&A^{\prime}B^{\prime} \end{array}
「三平方の定理」を使って
「2点間の距離」を求めると
後は式変形をすれば求めることができます。
\begin{array}{llllll} \displaystyle PQ&=&\displaystyle \sqrt{(x_q-x_p)^2+(y_q-y_p)^2} \end{array}
\begin{array}{llllll} AB^2&=& \displaystyle \left( 1-\cos(α+β) \right)^2+\sin^2(α+β) \\ \\ A^{\prime}B^{\prime \, 2} &=&\displaystyle \left( \cos β - \cos (-α) \right)^2 + \left(\sin β - \sin (-α) \right)^2 \end{array}
\begin{array}{cccllllll} \displaystyle AB&=&A^{\prime}B^{\prime} \\ \\ \displaystyle\left( AB \right)^2 &=&\displaystyle\left( A^{\prime}B^{\prime} \right)^2 \end{array}
\begin{array}{llllll} \displaystyle &&\displaystyle \left( 1-\cos(α+β) \right)^2+\sin^2(α+β) \\ \\ &=& 1-2\cos(α+β)+\cos^2(α+β)+\sin^2(α+β) \\ \\ &=&1-2\cos(α+β)+1 \end{array}
\begin{array}{llllll} &&\displaystyle \left( \cos β - \cos (-α) \right)^2 \\ \\ &=&\cos^2 β -2\cos β \cos (-α) +\cos^2 (-α) \\ \\ \\ &&\left(\sin β - \sin (-α) \right)^2 \\ \\ &=&\sin^2 β -2\sin β\sin (-α) +\sin^2 (-α) \end{array}
\begin{array}{llllll} \displaystyle && \displaystyle \left( \cos β - \cos (-α) \right)^2 + \left(\sin β - \sin (-α) \right)^2 \\ \\ &=& 1-2\Bigl( \cos β \cos (-α)+\sin β\sin (-α) \Bigr) +1\end{array}
このパターンだと余弦定理はいらないですね。
\mathrm{sinc} 関数
これも本筋からずれるので適当に。
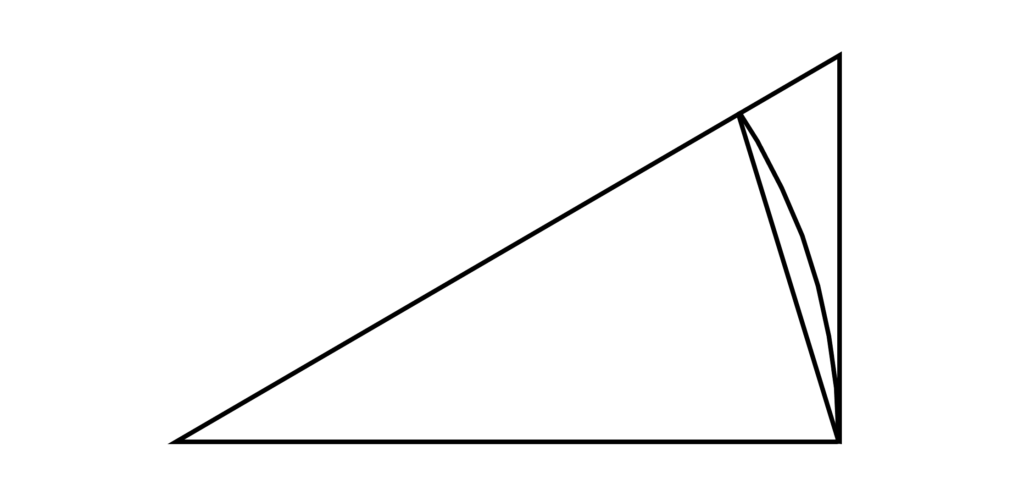
角度 θ 底辺 a とし
二等辺三角形・扇型・直角三角形の面積
これらを比較してみると
\begin{array}{rllllll} \displaystyle πr^2 &&円 \\ \\ \displaystyle \frac{θ}{2π}πr^2 &&扇形 \end{array}
\begin{array}{llllll} \displaystyle \displaystyle\frac{1}{2}a\sin θ &<& \displaystyle\frac{1}{2} θa^2 &<&\displaystyle\frac{1}{2} a\tan θ \end{array}
こうなるので
邪魔な a を消すために底辺 1 とし
\begin{array}{rrcrrrrrrrrl} \displaystyle\frac{1}{2}a\sin θ &<& \displaystyle\frac{1}{2} θa^2 &<&\displaystyle\frac{1}{2}\tan θ \\ \\ \sin θ &<& θ &<&\displaystyle\tan θ \\ \\ 1&<&\displaystyle \frac{θ}{\sin θ} &<&\displaystyle\frac{\tan x}{\sin θ} \end{array}
\begin{array}{llllll} \displaystyle \tan x&=& \displaystyle\frac{\sin x}{\cos x} \\ \\ \displaystyle\frac{\tan x}{\sin θ}&=& \displaystyle\frac{1}{\cos x} \end{array}
\begin{array}{llllll} \displaystyle \cos θ &<& \displaystyle \frac{\sin θ}{θ} &<& 1 \\ \\ \displaystyle \cos x &<& \displaystyle \frac{\sin x}{x} &<& 1 \end{array}
求めたい関数が真ん中に来るよう式変形して
その後に「はさみうちの原理」を用いると
\begin{array}{llllll} \displaystyle \lim_{x\to 0} \cos x &=&1 \\ \\ \displaystyle \lim_{x\to 0} \frac{\sin x}{x} &=&1 \end{array}
まあこうなる感じ。
この応用として
\begin{array}{llllll} \displaystyle \frac{\cos x -1}{x} &=&\displaystyle \frac{\cos x -1}{x}\frac{\cos x+1}{\cos x+1} \end{array}
\sin 0=0 を利用する形で
\begin{array}{llllll} \displaystyle (\cos x -1)(\cos x+1) &=& \cos^2 x-1 \\ \\ &=&(1-\sin^2 x) -1 \\ \\ &=&\displaystyle-\sin^2 x \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \frac{\cos x -1}{x} &=&\displaystyle\frac{-\sin^2 x}{x(\cos x+1)} \\ \\ &=&\displaystyle-\frac{\sin x}{x}\frac{\sin x}{\cos x+1} \end{array}
\begin{array}{llllll} \displaystyle \lim_{x\to 0}\frac{\sin x}{x} &=&1 \\ \\ \displaystyle \lim_{x\to 0}\frac{\sin x}{\cos x+1} &=&0 \end{array}
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{\cos h -1}{h}&=&\displaystyle \lim_{h\to 0}-\frac{\sin h}{h}\frac{\sin h}{\cos h+1} \\ \\ &=& 0 \end{array}
これも求められます。
実は循環定義
↑ の \mathrm{sinc} 関数の導出ですが
実は問題があって
\begin{array}{llllll} \displaystyle πr^2 \end{array}
この「円の面積」なんですけど
実はこれ、求めるには \sin の微分が必要で
\begin{array}{llllll} \displaystyle \frac{\sin h}{h} \end{array}
これを解消しようとあれこれすると
今度は \mathrm{sinc} 関数が出てきたり
\sin の微分が必要になったりします。
なので
『面積には触りたくない』
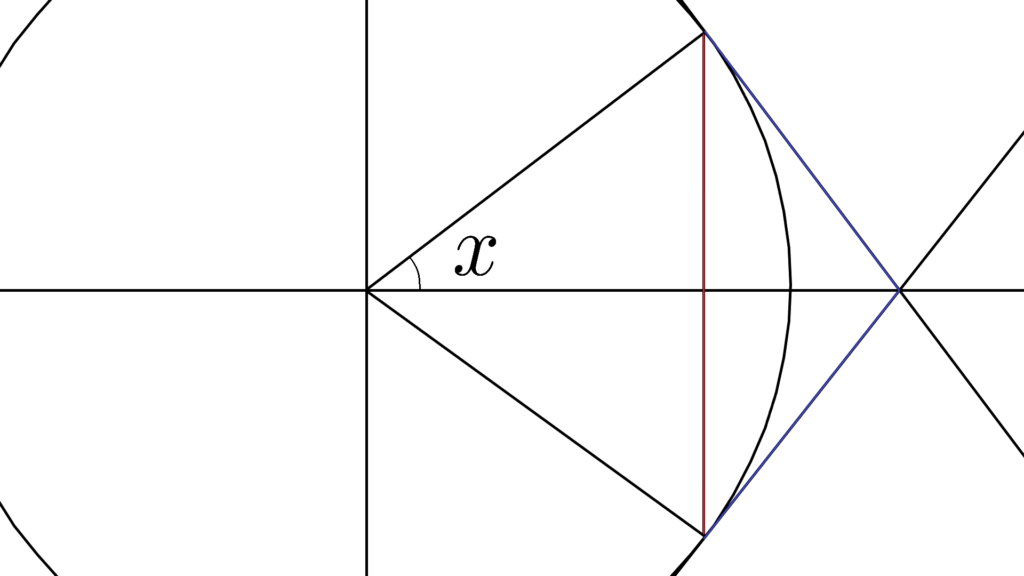
とまあこのような要望が見えてくるので
\begin{array}{ccccccllll} \textcolor{red}{縦線} && 弧 && \textcolor{royalblue}{接線} \\ \\ \displaystyle 2r\sin x &≤&2xr &≤& 2r\tan x \\ \\ \sin x &≤&x &≤& \tan x \end{array}
『面積』ではなく『長さ』を使って
この形を求めると
\begin{array}{cllllll} \displaystyle 弧&弧度法 \\ \\ 2x & \mathrm{radian} \end{array}
面積を求める必要がなくなるので
循環定義を解消できます。
\tan x
こっちはほぼ特殊な操作で導かれます。
\begin{array}{clrllll} (\tan x)^{\prime}&=&\displaystyle \frac{1}{\cos^2 x} \\ \\ \displaystyle \left( \frac{1}{\tan x} \right)^{\prime}&=&\displaystyle -\frac{1}{\sin^2 x} \end{array}
これは「積の微分」とか言われるやつと
「商の微分」の成果の一つから導かれる
\begin{array}{llllll} \displaystyle \left( f(x)g(x) \right)^{\prime} &=&f^{\prime}(x)g(x)+f(x)g^{\prime}(x) \end{array}
\begin{array}{llllll} \displaystyle \left( \frac{1}{f(x)} \right)^{\prime} &=& \displaystyle\frac{f^{\prime}(x)}{\left( f(x) \right)^2} \end{array}
\begin{array}{llllll} \displaystyle \left( \frac{f(x)}{g(x)} \right)^{\prime} &=&\displaystyle \frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{(g(x))^2} \end{array}
こういうやつを使うと
\begin{array}{llllll} \displaystyle \tan x&=&\displaystyle\frac{\sin x}{\cos x} \end{array}
\begin{array}{llllll} \displaystyle \left( \displaystyle\frac{\sin x}{\cos x} \right)^{\prime}&=&\displaystyle\frac{(\sin x)^{\prime}\cos x - \sin x(\cos x)^{\prime}}{\cos^2 x} \\ \\ &=&\displaystyle\frac{\cos x\cos x - \sin x(-\sin x)}{\cos^2 x} \\ \\ \\ \displaystyle \left( \displaystyle\frac{\cos x}{\sin x} \right)^{\prime}&=&\displaystyle\frac{(\cos x)^{\prime}\sin x - \cos x(\sin x)^{\prime}}{\sin^2 x} \\ \\ &=&\displaystyle\frac{(-\sin x)(\sin x) - \cos x\cos x}{\sin^2 x} \end{array}
直ちに導かれます。
指数関数 e^x,a^x
e^x に関しては
e の定義上必ずこうなるので当然なんですが
\begin{array}{llllll} \displaystyle \displaystyle \left( e^x \right)^{\prime}&=&e^x \\ \\ \displaystyle \left( a^x \right)^{\prime}&=&a^x\log a \end{array}
a^x も負けず劣らず簡単に導かれます。
\begin{array}{llllll} \displaystyle a^x&=&e^{\log a^x} \end{array}
\begin{array}{llllll} \displaystyle \left( e^{\log a^x} \right)^{\prime}&=&\displaystyle\left( \log a^x \right)^{\prime}e^{\log a^x} \\ \\ &=&\displaystyle\left( x\log a \right)^{\prime}e^{\log a^x} \\ \\ &=&\displaystyle e^{\log a^x} \log a \\ \\ &=&\displaystyle a^x \log a \end{array}
「合成関数の微分」を理解しておく必要はありますが。
e の定義
こいつは「微分で変化させない」ための定数として
\begin{array}{llllll} \displaystyle \left( a^x \right)^{\prime} &=&\displaystyle \lim_{h\to 0}\frac{a^{x+h}-a^x}{(x+h)-x} \\ \\ &=&\displaystyle \lim_{h\to 0}\frac{a^x(a^{h}-1)}{h} \\ \\ &=&\displaystyle \lim_{h\to 0}a^x\frac{(a^{h}-1)}{h} \end{array}
\begin{array}{llllll} \displaystyle \lim_{h\to 0} \frac{e^h-1}{h} &=&1 \end{array}
このように定義されているので
結果、微分した結果はすぐに求められます。
対数関数 \log x
e の定義を押さえておけば
これはわりと簡単に求められます。
\begin{array}{llllll} \displaystyle \displaystyle \left( \log x \right)^{\prime}&=&\displaystyle\frac{1}{x} \end{array}
結果はこう。
\begin{array}{llllll} e&=&\displaystyle \lim_{t\to \infty} \left( 1+\frac{1}{t} \right)^t \\ \\ e&=&\displaystyle \lim_{t\to 0} \left( 1+t \right)^{\frac{1}{t}} \end{array}
式変形していけば分かりますが
\begin{array}{llllll} \displaystyle \left( \log x \right)^{\prime}&=&\displaystyle\lim_{h\to 0} \frac{\log(x+h)-\log x}{(x+h)-x} \\ \\ &=&\displaystyle\lim_{h\to 0} \frac{1}{h}\log \left( \frac{x+h}{x} \right) \\ \\ \\ &=&\displaystyle\lim_{h\to 0} \frac{1}{h} \log \left( 1+\frac{h}{x} \right) \\ \\ &=&\displaystyle\lim_{h\to 0}\frac{x}{h}\frac{1}{x} \log \left( 1+\frac{h}{x} \right) \\ \\ \\ &=&\displaystyle\lim_{h\to 0} \frac{1}{x} \log \left( 1+\frac{h}{x} \right)^{\frac{x}{h}} \end{array}
\begin{array}{cllllll} \displaystyle\frac{h}{x} &&\to&&0 \\ \\ \displaystyle t &&\to && 0 \end{array}
\begin{array}{llllll} \displaystyle \displaystyle\lim_{h\to 0} \log \left( 1+\frac{h}{x} \right)^{\frac{x}{h}} &=&\log e \\ \\ \displaystyle\lim_{t \to 0} \log \left( 1+\frac{1}{t} \right)^{t} &=&\log e \\ \\ &=&1 \end{array}
適当に式変形していくと
自然とこの形に行き着きます。
補足しておくと
対数の底を a とおいても
\begin{array}{llllll}\displaystyle \displaystyle\lim_{h\to 0} \log_a \left( 1+\frac{h}{x} \right)^{\frac{x}{h}} &=&\log_a e \\ \\ \displaystyle\lim_{t \to 0} \log_a \left( 1+\frac{1}{t} \right)^{t} &=&\log_a e\end{array}
同様の結果が得られますが
\begin{array}{llllll} \displaystyle \log_a e &=&\displaystyle \frac{\log_e e}{\log_e a} \\ \\ &=&\displaystyle \frac{1}{\log_e a} \end{array}
その場合では定数の部分が 1 になりません。
(だいたい底の変換公式からこのように書かれます)
だから?って感じかもしれませんが
実はこれかなり重要なので覚えておきましょう。
「ネイピア数 e の定義」に関わります。
