|| ジョルダン測度を拡張したやつ
ほとんどの測度を求められる考え方
スポンサーリンク
目次
測度「長さとか面積とかのこと」
ジョルダン測度「ルベーグ測度の雛型」
ハルナック集合「ジョルダン非可測の代表例」
ルベーグ外測度「ジョルダン外測度を拡張したやつ」
区間と外測度「測度がちゃんと一致するか確認」
ルベーグ内測度「ルベーグ外測度で定義できる内測度」
区間と内測度「外測度と同様に一致するか確認」
ルベーグ測度「ルベーグ外測度を前提にする測度」
カラテオドリ条件「可測条件の簡易版」
可測集合「任意の区間とか開集合とか」
ルベーグ非可測「ちょっと考え辛いもの」
ヴィタリ集合「ルベーグ非可測の代表例」
可測関数「可測集合 → 可測集合の関数」
測度 Measure
|| 長さとか面積とか体積の総称
なんか「測れるやつ」全般のこと
\begin{array}{llllll} μ\Bigl( S \Bigr)&=&|S| \\ \\ \displaystyle μ\Bigl( [a,b)\Bigr)&=&(b-a) \\ \\ \displaystyle μ \Bigl( [a,b)×[c,d)\Bigr)&=&(b-a)\times (d-c) \end{array}
「個数」とかも測度の一種です。
詳しい話は別の記事にまとめてます。
ジョルダン測度 Jordan Measure
|| 長さとかの基本的な計算
直感的な「長さ・面積」とかの求め方
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b)\Bigr)&=&(b-a) \\ \\ \displaystyle μ \Bigl( [a,b)×[c,d)\Bigr)&=&(b-a)\times (d-c) \end{array}
ルベーグ測度の雛型になるやつです。
使える範囲には限りが有るんですが
これが問題を起こすことはほぼありません。
内測度と外測度
図形全体を覆う図形 S_{\mathrm{out}}
図形の中に全て収まる図形 S_{\mathrm{in}} から
\begin{array}{rccllllll} \displaystyle μ_{\mathrm{out}}(D)&=&\displaystyle\inf_{D⊂S_{\mathrm{out}}} μ(S_{\mathrm{out}}) \\ \\ \displaystyle μ_{\mathrm{in}}(D)&=&\displaystyle\sup_{S_{\mathrm{in}}⊂D} μ(S_{\mathrm{in}}) \end{array}
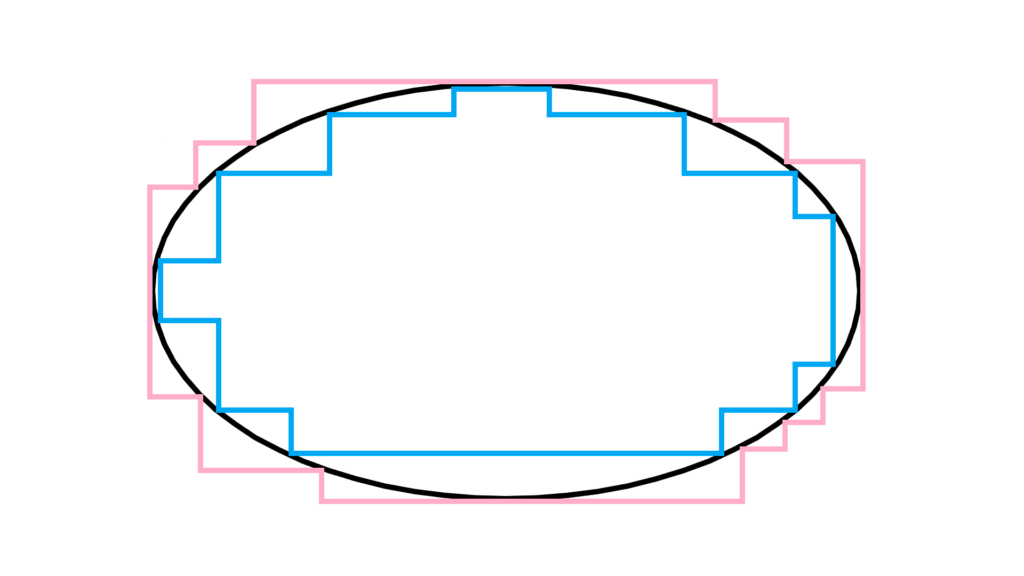
ジョルダン測度では
内測度と外測度はこのように定められています。
非常に直感的なので
これについては特に疑問は出ないかと。
ジョルダン測度で面積が求められない
定義関数を除いて
実践的な関数を扱う場合
「ジョルダン測度」ばかり使ったとしても
\begin{array}{llllll} \displaystyle μ(A)&≤&μ\Bigl( [a,b)\Bigr) \end{array}
問題が出ることはほぼありません。

しかし特殊な関数の測度を求める場合
特に「測度 0 」の図形を求める時なんかでは
\begin{array}{lclll} \mathrm{Set} && \displaystyle \mathrm{Square} &&\mathrm{Length} \\ \\ \\ H_0 && 1&&r_0=1 \\ \\ H_{n+1} && \displaystyle 4^{n+1} && \displaystyle r_{n+1}=\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \end{array}
「ジョルダン測度」じゃ求めることができない
\begin{array}{llllll} \displaystyle D(x)&=&\displaystyle \left\{ \begin{array}{cllllll} \displaystyle 1&&x∈Q \\ \\ 0&&x∈R\setminus Q \end{array} \right. \end{array}
そういう図形が
定義関数を使うとわりと簡単に作れたりします。
ハルナック集合 Harnack
|| ジョルダン非可測の代表例
正方形を4つに分解していく感じ
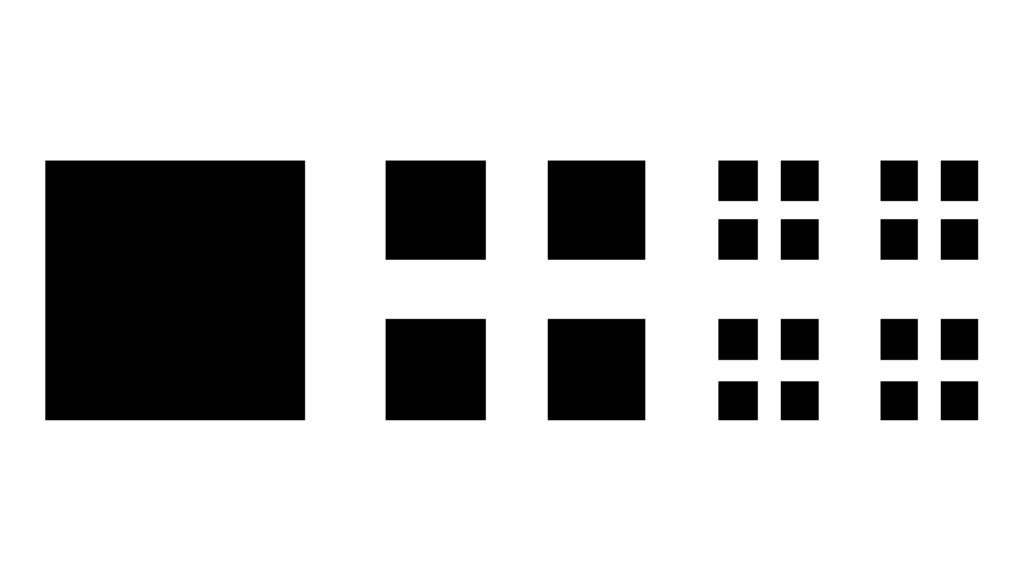
\begin{array}{lclll} \mathrm{Set} && \displaystyle \mathrm{Square} &&\mathrm{Length} \\ \\ \\ H_0 && 1&&r_0=1 \\ \\ H_1&& \displaystyle 4^1 && r_1=\displaystyle\frac{1}{2}\left( r_0-\frac{1}{4} \right) \\ \\ H_2&& \displaystyle 4^2 && r_2=\displaystyle\frac{1}{2}\left( r_1-\frac{1}{4^2} \right) \\ \\ && &\vdots& \\ \\ H_{n+1} && \displaystyle 4^{n+1} && \displaystyle r_{n+1}=\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \\ \\ && &\vdots& \end{array}
この時に最終的に出来上がる
「加算無限個の正方形」
\begin{array}{lcclllll} \displaystyle \lim_{n\to\infty} 4^{n+1}&=&\infty \\ \\ \displaystyle \lim_{n\to\infty} r_{n+1}&=&0 \end{array}
正確には
その「共通部分」となる正方形の集まりを
\begin{array}{llllll} H&=&\displaystyle \bigcap_{n=0}^{\infty}H_n \end{array}
ハルナック集合と言います。
\begin{array}{llllll} \displaystyle μ(H)&=&0 &&? \end{array}
で、実はこの「測度(面積)」が
ジョルダン測度では求められなくて
\begin{array}{llllll} \displaystyle 0&≤&μ(H)&≤&\displaystyle \frac{1}{4} \end{array}
具体的には
「外測度」が 0 より大きくなってしまいます。
補足しておくと
\begin{array}{llllll} \displaystyle \displaystyle\frac{1}{2}\left( r_0-\frac{1}{3} \right) \\ \\ \displaystyle\frac{1}{2}\left( r_0-\frac{1}{4} \right) \\ \\ \displaystyle \displaystyle\frac{1}{2}\left( r_0-\frac{1}{n} \right) \end{array}
「取り除く十字の辺の長さ」の値 n は
計算しやすいのでだいたい 4 が採用されます。
ジョルダン測度とハルナック集合
「正方形の個数」が無限に
「正方形の面積」が 0 に近づいていく
\begin{array}{lclll}\mathrm{Set} && \displaystyle \mathrm{Square} &&\mathrm{Length} \\ \\ \\ H_0 && 1 && r_0=1 \\ \\ && &\vdots& \\ \\ H_{n+1} && \displaystyle 4^{n+1} && \displaystyle r_{n+1}=\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \\ \\ && &\vdots& \end{array}
そのようになるよう作られたこれを
「ジョルダン測度」で求めようとすると
\begin{array}{llllll} μ_{\mathrm{in}}(A)&≤& \displaystyle μ(H) &≤& μ_{\mathrm{out}}(H_n) \end{array}
実は「外測度」と「内測度」が一致しないため
「測度」を求めることができません。
\begin{array}{llllll} \displaystyle μ_{\mathrm{in}}(A)&=&0 \\ \\ μ_{\mathrm{out}}(H_{n+1})&=&\displaystyle \left( \frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \right)^2\times 4^{n+1} \end{array}
具体的には
直感的には明らかに面積 0 なのに
\begin{array}{llllll} \displaystyle\frac{1}{4}&<&\cdots&<&μ(H_{n+2})&<&\displaystyle μ(H_{n+1}) \end{array}
「外測度」だけこのような値になるため
これ以上 0 に近付けない
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}μ(H_n)&=&0 &&× \end{array}
直感的には近づきそうなものですが
どうしてもこの値が残ってしまいます。
ハルナック集合の内測度
内測度はいくらでも小さくできるので
\begin{array}{llllll} \displaystyle 0&=&μ(A)&≤&μ(H) \end{array}
図形から
直感的にこのように置いていいです。
\begin{array}{llllll} \displaystyle 0&≤&μ(X) \end{array}
補足しておくと
まあ当然ですが
0 は全ての測度の内測度になります。
ハルナック集合の外測度
問題はこっちです。
といってもやることは式変形だけで
\begin{array}{lclll} \mathrm{Set} && \displaystyle \mathrm{Square} &&\mathrm{Length} \\ \\ \\ H_0 && 1&&r_0=1 \\ \\ H_{n+1} && \displaystyle 4^{n+1} && \displaystyle r_{n+1}=\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \end{array}
\begin{array}{llllll} \displaystyle r_{n+1}&=&\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \end{array}
正方形の一辺の長さを求めると
\begin{array}{llllll} \displaystyle r_{n+1}&=&\displaystyle\frac{1}{2}\left( r_n-\frac{1}{4^{n+1}} \right) \end{array}
\begin{array}{lclclllll} r_1&=& \displaystyle \frac{1}{2}\left( 1-\frac{1}{4} \right) \\ \\ r_2 &=& \displaystyle \frac{1}{2}\left( \frac{1}{2}\left( 1-\frac{1}{4} \right)-\frac{1}{4^2} \right) &=&\displaystyle \frac{1}{2^2}\left( 1-\frac{1}{4} -\frac{2}{4^2} \right) \\ \\ r_3 &=& \displaystyle \frac{1}{2}\left( \displaystyle \frac{1}{2^2}\left( 1-\frac{1}{4} -\frac{2}{4^2} \right)-\frac{1}{4^2} \right)&=&\displaystyle \frac{1}{2^3}\left( 1-\frac{1}{4} -\frac{2}{4^2}-\frac{2^2}{4^3} \right) \\ \\ && &\vdots \end{array}
\begin{array}{llllll} \displaystyle r_{n} &=& \displaystyle \frac{1}{2^n}\left( 1-\frac{1}{4} -\frac{2}{4^2}-\frac{2^2}{4^3}-\cdots -\frac{2^{n-1}}{4^n} \right) \\ \\ &=& \displaystyle \frac{1}{2^n}\left( 1-\frac{1}{4}\left(1+ \frac{2}{4}+\frac{2^2}{4^2}+\cdots +\frac{2^{n-1}}{4^{n-1}} \right) \right) \\ \\ &=& \displaystyle \frac{1}{2^n}\left( 1-\frac{1}{4}\left(1+ \frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^{n-1}} \right) \right) \end{array}
\begin{array}{rclllllll} S&=& \displaystyle 1+ \frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^{n-1}} \\ \\ \displaystyle \frac{1}{2}S &=& \displaystyle \frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^{n-1}}+\frac{1}{2^{n}} \end{array}
\begin{array}{llllll} \displaystyle S-\frac{1}{2}S &=&\displaystyle 1 - \frac{1}{2^{n}} \\ \\ \displaystyle S \left( 1-\frac{1}{2} \right) &=&\displaystyle 1 - \frac{1}{2^{n}} \\ \\ \displaystyle S&=& \displaystyle 2 \left( 1 - \frac{1}{2^{n}} \right) \end{array}
\begin{array}{llllll} \displaystyle r_{n} &=& \displaystyle \frac{1}{2^n}\left( 1-\frac{1}{4}\left(1+ \frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^{n-1}} \right) \right) \\ \\ &=&\displaystyle \frac{1}{2^n}\left( 1-\frac{1}{4}2 \left( 1 - \frac{1}{2^{n}} \right) \right) \\ \\ &=&\displaystyle \frac{1}{2^n}\left( 1-\frac{1}{2} \left( 1 - \frac{1}{2^{n}} \right) \right) \end{array}
ちょっと大変ですが
こうなるので
後は面積とその総和を求めれば
\begin{array}{llllll} \displaystyle r_n^2 \times 4^{n}&=&\displaystyle \left( \frac{1}{2^n}\left( 1-\frac{1}{2} \left( 1 - \frac{1}{2^{n}} \right) \right) \right)^2 4^{n} \\ \\ &=&\displaystyle \left( \frac{1}{2^n}\right)^2 \left( 1-\frac{1}{2} \left( 1 - \frac{1}{2^{n}} \right) \right)^2 \left(2^{n}\right)^2 \\ \\ &=&\displaystyle \left( 1-\frac{1}{2} \left( 1 - \frac{1}{2^{n}} \right) \right)^2 \end{array}
外測度の下限として
\begin{array}{llllll} \displaystyle μ(H_{n+1})&≤&μ(H_n) \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} r_n^2 \times 4^{n}&=&\displaystyle\lim_{n\to\infty} \left( 1-\frac{1}{2} \left( 1 - \frac{1}{2^{n}} \right) \right)^2 \\ \\ &=&\displaystyle \left( 1-\frac{1}{2} \left( 1 - 0 \right) \right)^2 \\ \\ \\ &=&\displaystyle \left( 1-\frac{1}{2} \right)^2 \\ \\ &=&\displaystyle \frac{1}{4} \end{array}
\begin{array}{llllll} \displaystyle \frac{1}{4}&≤&\cdots&≤&μ(H_{n+1})&≤&μ(H_n) \end{array}
このような関係が求められます。
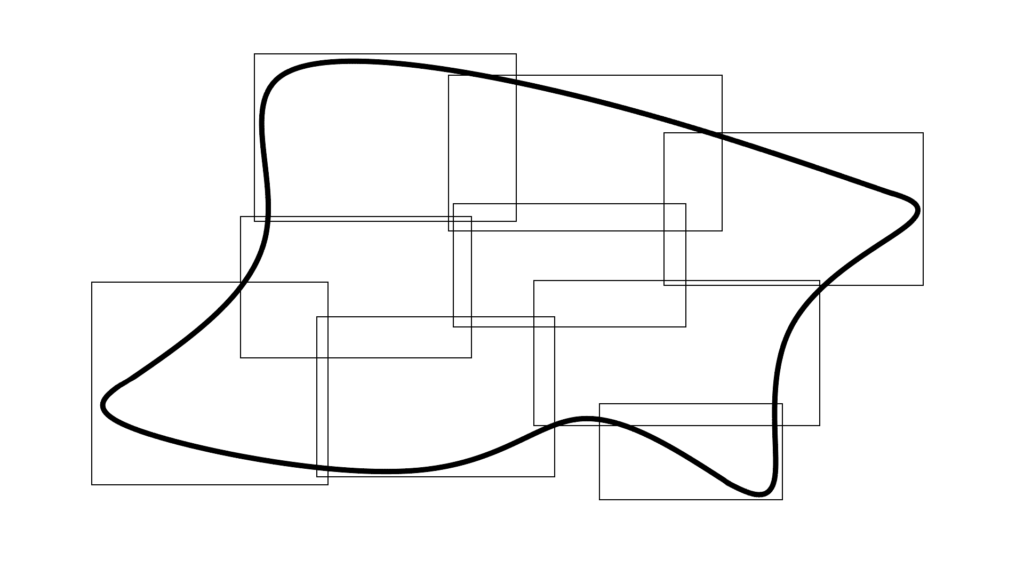
ルベーグ外測度 Lebesgue Outer
|| 長方形で覆ったやつの下限
「領域」で作った「長方形の集まり」の下限
\begin{array}{cccllllll} \displaystyle D&=&[a,b)\times [c,d) \\ \\ μ(D)&=&(b-a)(d-c) \end{array}
\begin{array}{llllll} \displaystyle μ^{*}(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \end{array}
D は測度を求めたい図形を意味する有界な集合
D_k は「図形 D 」をカバーできる
長方形を定義する「領域 \mathrm{Domain} 」とします。
\begin{array}{llllll} \displaystyle μ^*(D) \end{array}
この時の「測度 μ^* 」が「ルベーグ外測度」です。
( S_{\mathrm{out}} を分割したジョルダン外測度)
補足しておくと
μ(D_k) なんですが
\begin{array}{cclllll} \displaystyle μ\Bigl( [a,b)\Bigr)&=&b-a \\ \\ \Bigl|[a,b) \Bigr|&=&b-a \\ \\ \mathrm{vol}\Bigl( [a,b)\Bigr) &=&b-a \end{array}
\begin{array}{llllll} \displaystyle \mathrm{vol}(D_k)&=&(b_1-a_1)(b_2-a_2)\cdots \end{array}
これはこんな風に表現されることもあります。
(基本区間と呼ばれることがあります)
ジョルダン外測度との違い
ジョルダン外測度は「カバーできる図形 S_{\mathrm{out}} の全形」
ルベーグ外測度は「個々の図形 D_k の集まり」
\begin{array}{llllll} \displaystyle μ_{\mathrm{jordan}}(D)&=&\displaystyle\inf_{D⊂S_{\mathrm{out}}} μ(S_{\mathrm{out}}) \\ \\ \displaystyle μ_{\mathrm{lebesgue}}(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right)\end{array}
とまあそんな具合なので
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\bigcup_{k=1}^{n}D_k &&←&&\displaystyle S_{\mathrm{out}} \end{array}
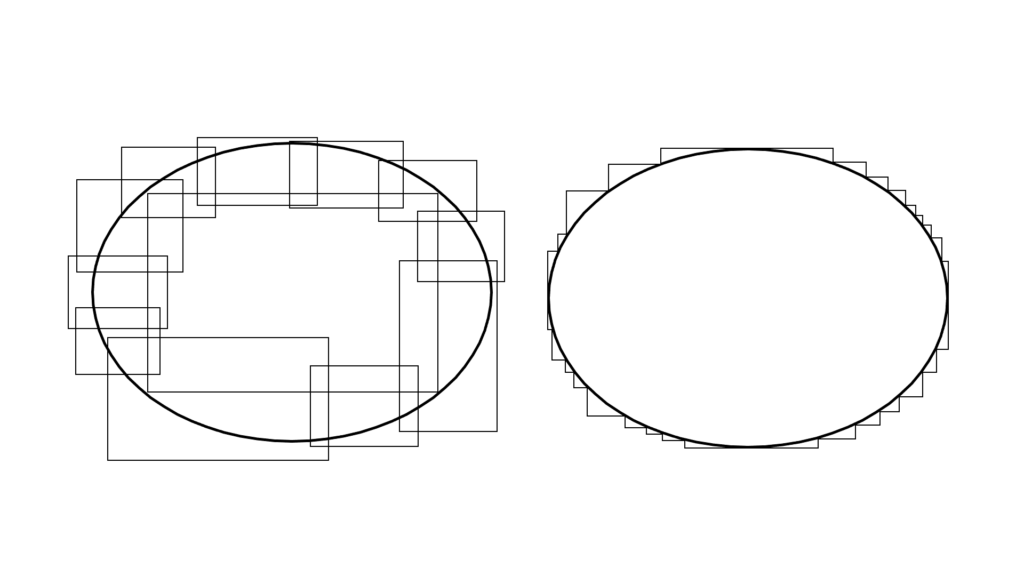
\begin{array}{llllll} \displaystyle μ(D_1)+μ(D_2)+\cdots+μ(D_n)+\cdots&&←&&μ(S_{\mathrm{out}}) \end{array}
ルベーグ測度の方が細かいというのは
数式からすぐに読み取れると思います。
実際
ルベーグ測度側からは図形を寄せれるので
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\bigcup_{k=1}^{n}D_k &→&\displaystyle S_{\mathrm{out}} \end{array}
「ルベーグ可測である」ということが
「ジョルダン可測である」ことも意味する
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\bigcup_{k=1}^{n}D_k &=&\displaystyle S_{\mathrm{out}} \end{array}
この「ジョルダン外測度の拡張」という感覚も
視覚的に明らかだと分かると思います。
(厳密な話は拡張定理の記事を参照)
区間とルベーグ外測度
直感的には ↓ は明らかですが
\begin{array}{llllll} \displaystyle μ^*(I)&=&μ(I) \\ \\ &=&b-a \end{array}
ルベーグ外測度の定義が複雑なので
\begin{array}{llllll} \displaystyle μ^{*}(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \\ \\ \displaystyle μ^{*}(I)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) \end{array}
本当にきちんとこうなるのか
\begin{array}{llllll} \displaystyle \displaystyle μ^*(I)&=&μ(I) \end{array}
念のため確認しておきます。
区間とルベーグ外測度の一致
ジョルダン外測度
ルベーグ外測度の双方で
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b)\Bigr)&=&b-a \\ \\ \displaystyle μ\Bigl( [a_1,b_1)\times [a_2,b_2) \Bigr)&=&(b_1-a_1)(b_2-a_2) \end{array}
これはこう定義されているわけですが
\begin{array}{llllll} \displaystyle μ(I)&=&\displaystyle\inf_{I⊂S_{\mathrm{out}}} μ(S_{\mathrm{out}}) \end{array}
\begin{array}{llllll} \displaystyle μ(I)&=&\inf μ\Bigl( [a,b+ε)\Bigr) &&∀ε>0 \\ \\ &=&\inf \Bigl( b -a+ε \Bigr) &&∀ε>0 \\ \\ &=&b-a \end{array}
ジョルダン外測度とは異なり
\begin{array}{llllll} \displaystyle \displaystyle μ^{*}(I)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) \end{array}
ルベーグ外測度の定義では
区間 I は分割されてしまっています。
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&b-a \end{array}
なので本当にこうなるのか
この時点ではまだ不明
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) \\ \\ &=&b-a \end{array}
きちんとこの結果になるよう計算が可能かは
確認しないと分かりません。
まあ一致するだろう
まだ分かっていないと言っても
直感的には明らかに成立するので
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&b-a \end{array}
これを示すために
\begin{array}{llllll} \displaystyle && μ^{*}(I)&=&μ(I) \\ \\ μ(I)&≤&μ^{*}(I)&≤&μ(I)&≤&μ^{*}(I) \end{array}
例えば
こんな感じにならないか確認してみます。
そこで
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&μ(I) \end{array}
サッとやりたいので
まずこれを考えてみたいんですが
これはパッと思いつきそうで思いつきません。
\begin{array}{llllll} μ(I)&≤&μ^{*}(I)&≤&μ(I) \\ \\ μ^{*}(I)&≤&μ(I)&≤&μ^{*}(I) \end{array}
でもこっちならなんとか行けそうなので
とりあえずこっちを採用して話を進めていきます。
区間の測度を下から抑える
というわけで事実を確認していくと
\begin{array}{llcllll} \displaystyle \displaystyle μ^{*}(I)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) \\ \\ &≤&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \end{array}
まずこの関係から
外測度の右辺が下限をとる以上
\begin{array}{llllll} \displaystyle [0,3)&=&[0,1)∪[1,2)∪[2,3)&&μ(I)=\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \\ \\ &=&[0,2)∪[2,3) &&μ(I)=\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \\ \\ &=&[0,1)∪[0,2)∪[0,3) &&μ(I)≤\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \end{array}
適当な右半開区間 I_n=[a_n,b_n) を考えると
\begin{array}{llllll} \displaystyle a&≤&a_n \\ \\ &&a_n&≤&b_n \\ \\ &&&& b_n&≤&b \end{array}
\begin{array}{llllll} \displaystyle I&=&I_1∪I_2∪\cdots ∪I_n \\ \\ &=&[a_1,b_1)∪[a_2,b_2)∪\cdots ∪[a_n,b_n) \end{array}
\begin{array}{llllll} \displaystyle \frac{k}{n} \end{array}
\begin{array}{llrllll} \displaystyle a_k &=&\displaystyle a+\frac{k-1}{n}b \\ \\ b_k &=&\displaystyle \frac{k}{n}b \end{array}
例えばこのようにすれば
\begin{array}{llllll} \displaystyle μ(I)&=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \end{array}
この関係は成立し得るので
\begin{array}{cccllllll} μ^{*}(I)&≤&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) &=&μ(I)\end{array}
ルベーグ外測度が下限をとる以上
以下の前提の元では
\begin{array}{cclll} \displaystyle \left( \begin{array}{ccclll} \displaystyle i≠j&\to&I_i≠I_j \\ \\ \displaystyle I&=&\displaystyle\bigcup_{n=1}^{\infty}I_n \end{array} \right) \\ \\ ↓ \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k)&=&μ(I) \end{array}
\begin{array}{llllll} \displaystyle μ^{*}(I)&≤&μ(I) \end{array}
この関係が得られます。
区間の測度を上から抑える
区間を上から抑えるには
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) \\ \\ \displaystyle &&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) &<&μ^{*}(I)+ε \end{array}
単純に考えるなら
任意の実数 ε>0 を使って
このような形を考える必要があるわけですが
\begin{array}{llllll} \displaystyle \inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) &<&μ^{*}(I)+ε \end{array}
これだけではまだちょっと不足
というわけで
事実を列挙してみると
\begin{array}{llllll} \displaystyle I&⊆&\displaystyle\bigcup_{k=1}^{\infty}I_k \end{array}
この事実から
\begin{array}{llllll} \displaystyle μ(I)&≤&\displaystyle\sum_{k=1}^{\infty}μ(I_k) \end{array}
これが導かれるので
[a,b) を分割した
右半開区間 [a_n,b_n) を I_n だとすれば
\begin{array}{llllll} \displaystyle \inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) &≤&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \end{array}
さっき示したように
\begin{array}{ccc} \displaystyle \sum_{n=1}^{\infty} \frac{1}{2^n} &=&\displaystyle \lim_{n\to\infty}\frac{\frac{1}{2}- \left( \frac{1}{2} \right)^n }{1-\frac{1}{2}} \\ \\ &=&1 \end{array}
\begin{array}{llllll} \displaystyle [0,1)&=&\displaystyle \left[ 0,\frac{1}{2} \right)∪\left[ \frac{1}{2},\frac{1}{2}+\frac{1}{4} \right)∪ \left[ \frac{1}{2}+\frac{1}{4},\frac{1}{2}+\frac{1}{4} +\frac{1}{8} \right) ∪\cdots \end{array}
例えばこのようにすれば
これらの同値関係は成立し得ることから
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) &=& \displaystyle \inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) &<&μ^{*}(I)+ε \end{array}
I_n が [a,b) を分割した右半開区間であれば
この関係が成立します。
そしてこの結果から
\begin{array}{llllll} μ(I)&≤&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) &<&μ^{*}(I)+ε \end{array}
この関係が導かれます。
同じ前提で上と下から抑えられる
「ルベーグ測度」は『下限をとる』ので
\begin{array}{cclll} \displaystyle \left( \begin{array}{ccclll} \displaystyle i≠j&\to&I_i≠I_j \\ \\ \displaystyle I&=&\displaystyle\bigcup_{n=1}^{\infty}I_n \end{array} \right) \\ \\ ↓ \end{array}
\begin{array}{llllll} \displaystyle \inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \right) &=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}μ(I_k) \end{array}
区間 I=[a,b) が単純な形であることから
I_n が [a,b) を分割する半開区間である
この前提が採用出来て
\begin{array}{llllll} μ^{*}(I)&≤&μ(I)&<&μ^{*}(I)+ε \end{array}
その結果として
測度の間にはこのような関係が導かれます。
そしてここから
\begin{array}{llllll} μ^{*}(I)&≤&μ(I)&<&μ^{*}(I)+ε \\ \\ μ^{*}(I)-μ^{*}(I)&≤&μ(I)-μ^{*}(I)&<&μ^{*}(I)-μ^{*}(I)+ε \\ \\ 0&≤&μ(I)-μ^{*}(I)&<&ε \end{array}
この関係が導かれて
\begin{array}{llllll} \displaystyle |μ(I)-μ^{*}(I)|&<&ε \end{array}
「極限の定義」より
\begin{array}{llllll} \displaystyle μ^{*}(I)-μ(I)&\to&0 \\ \\ μ^{*}(I)&\to&μ(I) \end{array}
この結果を導くので
\begin{array}{llllll} \displaystyle μ^{*}(I)&=&μ(I) \\ \\ &&μ(I)&=&b-a \end{array}
半開区間 I のルベーグ外測度 μ^{*}(I) は
下限をとると μ(I)=b-a に収束する
ということが分かります。
ルベーグ内測度 Lebesgue Inner
|| 切り抜いて求める感じ
求めたい図形全体をカバーできる
「線」や「長方形 \mathrm{Rectangle} 」から

\begin{array}{llllll} \displaystyle μ_*(D)&=&μ^*(\mathrm{Rect})-μ^*(D^c∩\mathrm{Rect}) \end{array}
求めたい図形の補集合を引いて求める感じ。
感覚的には
内測度というより外測度の感覚に近いですが
\begin{array}{llllll} \displaystyle D^c∩\mathrm{Rect} \end{array}
この部分は外測度しか分からないため
(実際より大きい → 合わせていく)

\begin{array}{rccllllll} μ^*(\mathrm{Rect})-μ^*(D^c∩\mathrm{Rect})&≤& μ(D) \\ \\ μ_*(D)&≤& μ(D) \end{array}
求めたい「図形 D の測度 μ(D) 」との大小関係は
必ずこうなります。
これは
「長方形 \mathrm{Rect} 」が内部にある場合でも同様で
\begin{array}{llllll} \displaystyle \mathrm{Rect}&⊂&D \end{array}
\begin{array}{llllll} \displaystyle D^c∩\mathrm{Rect}&=&∅ \end{array}
\begin{array}{rccllllll} μ^*(\mathrm{Rect})-μ^*(D^c∩\mathrm{Rect})&≤& μ(D) \\ \\ μ^*(\mathrm{Rect})-μ^*(∅)&≤& μ(D) \\ \\ μ_*(\mathrm{Rect})&≤& μ(D) \end{array}
この関係がこうなることから
\begin{array}{rccllllll} μ^*(\mathrm{Rect})-μ^*(D^c∩\mathrm{Rect})&≤& μ(D) \end{array}
この形は崩れません。
ということはつまり
\begin{array}{cccllllll} \displaystyle D&⊂&\mathrm{Rect} \\ \\ \mathrm{Rect}&⊂&D \end{array}
このどちらの条件でも
\begin{array}{rccllllll} μ^*(\mathrm{Rect})-μ^*(D^c∩\mathrm{Rect})&≤& μ(D) \end{array}
この関係は常に成立します。
(後述する可測の条件で使える)
区間とルベーグ内測度
ルベーグ外測度と区間の関係が分かってるので
\begin{array}{llllll} \displaystyle μ_*\Bigl( [a,b) \Bigr)&=&b-a \end{array}
ここに落ち着くのはまあ明らか。
とはいえこの時点ではまだ不明なので
きちんと示していきます。
というわけで確認しておくと
\begin{array}{rccllllll} μ_*(I)&=&μ^*(X)-μ^*(I^c∩X) \\ \\ &&μ^*(X)-μ^*(I^c∩X)&≤& μ(I)&=&b-a \end{array}
ルベーグ内測度の定義はこうです。
で、区間 [a,b) をカバーする図形 X は
\begin{array}{llllll} \displaystyle X&=&[a,b+ε) \end{array}
なんでもいいので
とりあえず適当にこれを採用
\begin{array}{llllll}I^c&=&(-\infty,a)∪[b,\infty) \\ \\ \displaystyle I^c∩X&=&[b,b+ε) \end{array}
この上で
集合の関係を整理していくと
\begin{array}{llllll} \displaystyle μ^*(X)&=&(b+ε)-a \\ \\ μ^*(I^c∩X)&=&(b+ε)-b \end{array}
\begin{array}{llllll} \displaystyle μ^*(X)-μ^*(I^c∩X)&=&-a-(-b) \\ \\ &=&b-a \end{array}
後はそのまま計算するだけで
この結果に至ります。
区間のルベーグ外測度が分かってるので
\begin{array}{llllll} \displaystyle μ^*\Bigl( [a,b) \Bigr)&=&b-a \end{array}
特に疑問の余地は無いかと。
ルベーグ測度 Lebesgue Measure
|| ジョルダン測度の範囲を広げたやつ
ルベーグ外測度に完全加法性を与えたもの
(ルベーグ外測度は一般には完全加法性を持たない)
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} A∩B=∅ \\ \\ \displaystyle A,B∈σ \\ \\ A∪B∈σ \end{array} \right) &\to& μ^*(A∪B)=μ^*(A)+μ^*(B) \end{array}
この μ^* を「ルベーグ測度」と言います。
「ルベーグ可測」の条件は
\begin{array}{llllll} \displaystyle μ^*(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \\ \\ μ_*(D) &=&μ^*(\mathrm{Fig}_{\mathrm{simple}})-μ^*(D^c∩\mathrm{Fig}_{\mathrm{simple}}) \end{array}
\begin{array}{llllll} \displaystyle μ_*(D)&=&μ^*(D) \end{array}
「ジョルダン測度」と同様
「外測度と内測度が一致する」という
\begin{array}{llrllll} \displaystyle μ(D)&≤&\displaystyle \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \\ \\ &↓ \\ \\ μ^*(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \end{array}
完全加法性から来る
自然なものが与えられています。
カラテオドリ条件 Carathéodory
|| ルベーグ可測の代表的な条件
可測集合を定義する簡単な条件
\begin{array}{llllll} \displaystyle μ^*(S)&=&μ^{*}(S∩D)+μ^{*}(S∩D^c) \end{array}
D が「可測であるか判定したい図形」
μ^{*} は「ルベーグ外測度」で
あらゆる S⊆R^n でこの関係が成り立つ時
「集合 D は可測である」となります。
補足しておくと
この条件で出てくる D と S は
可測集合に限定されていません。
なので問題が出そうですが
「図形全体をカバーする集合 S 」が
「可測集合ではない」としても
\begin{array}{llllll} \displaystyle S∩D&⊆&D \\ \\ S∩D^c&⊆&D^c \end{array}
共通部分をとるので
判定したい図形 D の要素のみで議論できます。
( S に入るかもしれない変な要素は除外されるので)
カラテオドリ条件の役割
「可測集合」の定義は
「完全加法族である」ことの他に
\begin{array}{llllll} \displaystyle μ^*(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \\ \\ μ_*(D) &=&μ^*(\mathrm{Fig})-μ^*(D^c∩\mathrm{Fig}) \end{array}
外測度と内測度が一致する
なんてものもあるんですが
これはこのまま扱うのは大変
\begin{array}{llllll} \displaystyle μ^*(D)&=&μ_*(D) \end{array}
どこから手を付ければ良いのか
いまいちよく分かりません。
そこで
この条件を具体化して簡略化したのが
「カラテオドリ条件」で
\begin{array}{llllll} \displaystyle μ^*(S)&=&μ^{*}(S∩D)+μ^{*}(S∩D^c) \end{array}
この条件のおかげで
「可測であるかどうか」が
簡単に判定できるようになっています。
条件の導出
これはわりとそのままで
\begin{array}{cccllllll} \displaystyle \mathrm{Fig}&⊂&R \\ \\ \mathrm{Fig}&⊂&R^2 \\ \\ &\vdots \\ \\ \mathrm{Fig}&⊂&R^n \end{array}
範囲をどのようにとっても
\begin{array}{llllll} \displaystyle μ_*(D) &=&μ^*(\mathrm{Fig})-μ^*(D^c∩\mathrm{Fig}) \\ \\ &&μ^*(\mathrm{Fig})-μ^*(D^c∩\mathrm{Fig}) &≤& μ(D) \end{array}
「内測度」と
\begin{array}{ccccclll} D&⊂&\mathrm{Fig} \\ \\ \displaystyle D&=&D∩\mathrm{Fig} \end{array}

\begin{array}{ccccclll} \mathrm{Fig}&⊂&D \\ \\ \displaystyle \mathrm{Fig}&=&D∩\mathrm{Fig} \\ \\ \displaystyle ∅&=&D^c∩\mathrm{Fig} \end{array}
\begin{array}{llllll} \displaystyle D∩\mathrm{Fig}&⊂&D \\ \\ D∩\mathrm{Fig}&⊂&\mathrm{Fig} \end{array}
この単純な関係から
\begin{array}{cccllllll} \displaystyle \displaystyle D&=&D∩\mathrm{Fig} \\ \\ \displaystyle μ^*(D)&=&\displaystyle μ^*(D∩\mathrm{Fig}) \\ \\ \\ \displaystyle \mathrm{Fig}&=&D∩\mathrm{Fig} \\ \\ \displaystyle μ^*(\mathrm{Fig})&=&\displaystyle μ^*(D∩\mathrm{Fig}) \\ \\ \displaystyle μ^*(∅)&=&\displaystyle μ^*(D^c∩\mathrm{Fig}) \end{array}
「外測度」より
\begin{array}{ccc} \displaystyle μ^*(D)&=&μ_*(D) \\ \\ μ^*(D∩\mathrm{Fig})&=&μ^*(\mathrm{Fig})-μ^*(D^c∩\mathrm{Fig}) \end{array}
「可測」の条件から
ここが着地なので
\begin{array}{llllll} \displaystyle μ^*(\mathrm{Fig})&=&μ^*(D∩\mathrm{Fig})+μ^*(D^c∩\mathrm{Fig}) \end{array}
「任意の \mathrm{Fig} で成立する」ものとして
関係自体は簡単に導けます。
( \mathrm{Fig} がなんでもいい理由は別記事で)
代表的な可測集合
この可測条件を使うと
\begin{array}{cllllll} \displaystyle X&⊂&R \\ \\ X&=&X∩R \\ \\ ∅ &=&X∩R^c \end{array}
\begin{array}{llllll} \displaystyle μ^*(X∩R)+μ^*(X∩R^c)&=&μ^*(X)+μ^*(∅) \\ \\ &=&μ^*(X) \end{array}
こうやれば
「実数 R 」が可測集合である
ということがすぐに導けます。
可測集合の補集合もまた可測集合
カラテオドリ条件を使うと
これもすぐに導けます。
\begin{array}{llllll} \displaystyle μ^*(\mathrm{Fig})&=&μ^*(D∩\mathrm{Fig})+μ^*(D^c∩\mathrm{Fig}) \end{array}
というのも
「集合 D は可測である」を前提とすると
\begin{array}{llllll} μ^*(D^c∩\mathrm{Fig})+μ^*((D^c)^c∩\mathrm{Fig}) \end{array}
\begin{array}{llllll} \displaystyle (D^c)^c&=&D \end{array}
補集合のとこを変形するだけで
\begin{array}{llllll} &&μ^*(D^c∩\mathrm{Fig})+μ^*((D^c)^c∩\mathrm{Fig}) \\ \\ \\ &=&μ^*(D^c∩\mathrm{Fig})+μ^*(D∩\mathrm{Fig}) \\ \\ &=&μ^*(D∩\mathrm{Fig})+μ^*(D^c∩\mathrm{Fig}) \end{array}
これが得られますから
「集合 D がルベーグ可測である」ため
\begin{array}{llllll} \displaystyle μ^*(\mathrm{Fig})&=&μ^*(D∩\mathrm{Fig})+μ^*(D^c∩\mathrm{Fig}) \\ \\ &=&μ^*(D^c∩\mathrm{Fig})+μ^*((D^c)^c∩\mathrm{Fig}) \end{array}
結果、明らかにこうなります。
可測集合の和集合も可測
長くなるので詳細を省くと
\begin{array}{llllll} \displaystyle μ^*(X)&=&μ^*(A∩X)+μ^*(A^c∩X) \\ \\ μ^*(X)&=&μ^*(B∩X)+μ^*(B^c∩X) \end{array}
A,B は可測なのでこう
\begin{array}{llllll} \displaystyle μ^*\Bigl((A∪B)∩X \Bigr)+μ^*\Bigl((A∪B)^c∩X \Bigr) \end{array}
これが μ^*(X) と一致するのがゴール
\begin{array}{llllll} (A∪B)^c&=&A^c∩B^c \end{array}
この辺りが分かってるので
集合の演算から
\begin{array}{llllll} \displaystyle μ^*(X)&=&μ^*(A∩X)+μ^*(A^c∩X) \\ \\ μ^*(X)&=&μ^*(B∩X)+μ^*(B^c∩X) \end{array}
\begin{array}{llllll} μ^*(A^c∩X)&=&μ^*\Bigl( B∩(A^c∩X) \Bigr)+μ^*\Bigl( B^c∩(A^c∩X) \Bigr) \\ \\ &=&μ^*\Bigl( B∩A^c∩X \Bigr)+μ^*\Bigl( (B∪A)^c∩X \Bigr) \end{array}
この式はこんな感じになりますから
後はゴールに寄せていくと
\begin{array}{llllll} \displaystyle μ^*(X)&=&μ^*(A∩X)+μ^*(A^c∩X) \\ \\ &=&\textcolor{pink}{μ^*(A∩X)+μ^*\Bigl( B∩A^c∩X \Bigr)}+μ^*\Bigl( (B∪A)^c∩X \Bigr) \end{array}
整理したいこの部分が
\begin{array}{llllll} \displaystyle μ^*(A∩X)+μ^*\Bigl( B∩A^c∩X \Bigr)&=&μ^* \Bigl( (A∩X) ∪(B∩A^c∩X) \Bigr) \end{array}
\begin{array}{llllll} \displaystyle (A∩X) ∪(B∩A^c∩X)&=&\displaystyle \Bigl( A∪(B∩A^c) \Bigr)∩X \\ \\ &=&(A∪B)∩X \end{array}
うまいことこうなるため
\begin{array}{llllll} \displaystyle μ^*(X)&=&μ^*(A∩X)+μ^*(A^c∩X) \\ \\ &=&μ^*(A∩X)+μ^*\Bigl( B∩A^c∩X \Bigr)+μ^*\Bigl( (B∪A)^c∩X \Bigr) \\ \\ &=&\displaystyle μ^*\Bigl( (A∪B)∩X\Bigr)+μ^*\Bigl((A∪B)^c∩X \Bigr) \end{array}
結果、こうなる。
だから可測集合の和集合は可測になります。
共通部分も当然のように可測
「集合の演算」から
\begin{array}{llllll} \displaystyle (A∩B)^c &=&A^c∪B^c \\ \\ (A^c∪B^c)^c &=&(A^c)^c∩(B^c)^c \\ \\ &=&A∩B \end{array}
着地より
\begin{array}{llllll} \displaystyle μ^*\Bigl( (A∩B)∩X \Bigr)+μ^*\Bigl( (A∩B)^c∩X \Bigr) \end{array}
可測集合の補集合が可測であることと
\begin{array}{llllll} \displaystyle μ^*(X)&=&μ^*(A∩X)+μ^*(A^c∩X) \\ \\ &=&μ^*(A^c∩X)+μ^*((A^c)^c∩X) \end{array}
和集合が可測であることから
\begin{array}{llllll} μ^*(X)&=&\displaystyle μ^*\Bigl((A∪B)∩X \Bigr)+μ^*\Bigl((A∪B)^c∩X \Bigr) \end{array}
\begin{array}{cccl} \displaystyle (A∩B)^c &=& A^c∪B^c \\ \\ A∩B &=&(A^c∪B^c)^c \end{array}
\begin{array}{llllll} μ^*(X)&=&\displaystyle μ^*\Bigl((A^c∪B^c)∩X \Bigr)+μ^*\Bigl((A^c∪B^c)^c∩X \Bigr) \\ \\ &=&\displaystyle μ^*\Bigl((A∩B)^c∩X \Bigr)+μ^*\Bigl((A∩B)∩X \Bigr) \end{array}
これもまた直ちに導かれます。
ちなみに
これと補集合が可測であることから
\begin{array}{llllll} \displaystyle A\setminus B&=&A∩B^c \end{array}
\begin{array}{llllll} μ^*(X) &=&\displaystyle μ^*\Bigl((A∩B^c)∩X \Bigr)+μ^*\Bigl((A∩B^c)^c∩X \Bigr) \\ \\ &=&\displaystyle μ^*\Bigl((A\setminus B)∩X \Bigr)+μ^*\Bigl((A\setminus B)^c∩X \Bigr) \end{array}
差集合が可測であることも導けます。
零集合ももちろん可測
これも簡単で
\begin{array}{cccllllll} \displaystyle C∩D&⊂&D \\ \\ μ(C∩D)&≤&μ(D) \\ \\ \\ C∩D^c&⊂&C \\ \\ μ(C∩D^c)&≤&μ(C) \end{array}
\begin{array}{llllll} \displaystyle μ(P)&=&0 \end{array}
\begin{array}{llllll} μ^*(C)&≤&\displaystyle μ^*(P∩C)+μ^*(P^c∩C) \end{array}
\begin{array}{llllll} \displaystyle μ^*(P∩C)+μ^*(P^c∩C) &≤&μ^*(P)+μ^*(P^c∩C) \\ \\ &≤&μ^*(P^c∩C) \\ \\ &≤&μ^*(C) \end{array}
\begin{array}{llllll} μ^*(C)&≤&\displaystyle μ^*(P∩C)+μ^*(P^c∩C)&≤&μ^*(C) \end{array}
すぐに導けます。
(詳細は別の記事で)
可測集合 Measurable Set
|| ルベーグ可測な集合のこと
\begin{array}{lccllll} \displaystyle μ^{*}(\mathrm{Point})&&←&&μ^{*}(\mathrm{Interval}) \\ \\ \displaystyle μ^{*}(\mathrm{Line})&&←&&μ^{*}(\mathrm{Interval}) \\ \\ \displaystyle μ^{*}(\mathrm{Area})&&←&&μ^{*}(\mathrm{Interval}) \end{array}
厳密には
「実数上の区間」について議論する場合
\begin{array}{rccllllll} \displaystyle \lim_{x\to a} f(x)-α&=&0 \\ \\ |f(x)-α|&<&ε &&\Bigl( |x-a|<δ\Bigr) \end{array}
もっと言うと
「極限」が使える環境を考える場合
「ボレル集合」の知識が必要なんですが
\begin{array}{llllll} \displaystyle \mathrm{Borel}(R) &&\to&& \displaystyle \left( \begin{array}{clllll} \displaystyle [a,b) \\ \\ (a,b) \\ \\ [a,b] \\ \\ \{a\} \\ \\ N \\ \\ Q \\ \\ R\setminus Q \end{array} \right) \end{array}
これは長くなるので別の記事で扱います。
(位相空間上で定義されるので説明が大変)
ルベーグ可測集合の集合は完全加法族
ルベーグ可測の定義上
完全加法性を持つのは当然なんですが
\begin{array}{rcrllllll} \displaystyle R∈L&\to&∅∈L \\ \\ D∈L &\to&D^c∈L \\ \\ D_n∈L &\to&\displaystyle \bigcup_{n=1}^{\infty}D_n∈L \end{array}
念のため確認しておくと
ルベーグ可測集合 D の集まりを L とすると
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
完全加法族の定義はこれなので
\begin{array}{llllll} \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} &&&& \begin{array}{rcrllllll} \displaystyle R∈L&\to&∅∈L \\ \\ D∈L &\to&D^c∈L \\ \\ D_n∈L &\to&\displaystyle \bigcup_{n=1}^{\infty}D_n∈L \end{array} \end{array}
まあ当然ではありますが
ルベーグ可測集合の集まり(集合族)は
完全加法族であると言えます。
ルベーグ非可測 Non-Measurable
|| 測度論が必要になる主な理由
ルベーグ外測度上で出てくる例外のこと
\begin{array}{llllll} \displaystyle μ^{*}(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \end{array}
これまでの話を考えると
なんかほとんど行けそうですが
「全部」いけるのか
みたいなことを考えると
ちょっと分かりませんよね。
まあ結論からいくと全部は無理なんですが
その無理なものって何?ってなると
\begin{array}{llllll} \displaystyle μ_*(X)&≠&μ^*(X) \end{array}
ちょっとよく分からないと思うので
これから紹介していきます。
ヴィタリ集合 Vitali Set
|| 非可測を実現するために作られた集合
「平行移動不変性」から導かれる集合 V のこと
\begin{array}{ccccrcccccccll} \displaystyle r+q &\equiv & r \mod Q && (r+q)-r ∈Q \\ \\ e &\not\equiv & π \mod Q && e-π\not\in Q \end{array}
「選択公理」を認めると定義可能な
\begin{array}{llllll} \displaystyle r+Q&=&\{r+q \mid q∈Q \} \end{array}
\begin{array}{llllll} \displaystyle R/Q&=&\{r+Q \mid r∈I \} \end{array}
剰余類 r+Q
剰余群 R/Q で定義されていて
\begin{array}{llllll} \displaystyle [r]&=&\displaystyle \left\{ \begin{array}{cllllll} \displaystyle r+q_1 &&\mathrm{Select} \\ \\ r+q_2 &&\mathrm{Select} \\ \\ &\vdots \end{array} \right. \end{array}
剰余類 r+Q の代表元 [r] の集まりとして
\begin{array}{llllll} \displaystyle V&=&\{ [r]∈r+Q \mid r+Q ∈R/Q \} \end{array}
「ヴィタリ集合」はこのように定義されています。
具体的には
\begin{array}{llllll} \displaystyle V&=&\{0,...,\log 2,...,\sqrt{2},...,e,...,π,...,e^{10},...\} \\ \\ V&=&\{1,...,\log 2+1,...,\sqrt{2}+3,...,e+0.1,...,π-2,...\} \end{array}
こういうのが「ヴィタリ集合」です。
(実際には横並びで書けません)
ヴィタリ集合の主な性質
これは以下の性質を持つように作られています。
\begin{array}{llllll} \displaystyle 0&<&\displaystyle \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V+q_n \right) &<&\infty \end{array}
\begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V+q_n \right) &=& \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) \end{array}
\begin{array}{llllll} \displaystyle i≠j&&\to&& V+q_i∩V+q_j=∅ \end{array}
これもこの記事で説明したかったんですが
ちゃんとやると長くなるので詳細は別の記事で
ルベーグ外測度は完全加法性を持たない
この「ヴィタリ集合」の存在から
\begin{array}{llllll} \displaystyle 0&<& \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V+q_n \right) &<&\infty \end{array}
「ルベーグ外測度 μ^* 」が
必ず「完全加法性を満たす」わけではない
\begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V+q_n \right)&=&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) \end{array}
\begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right)&=&μ^*(V)+μ^*(V)+\cdots \end{array}
そんな事実が導けます。
完全加法性の仮定と矛盾
確認しておくと
「互いに素」であることから
\begin{array}{llllll} \displaystyle i≠j&&\to&& V+q_i∩V+q_j=∅ \end{array}
感覚的には
「完全加法性」は問題なく仮定できるわけですが
\begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right)&=&μ^*(V)+μ^*(V)+\cdots \end{array}
詳細は省きますが
ヴィタリ集合の集まりは
\begin{array}{cccccccccll} \displaystyle μ^*\Bigl([0,1) \Bigr)&<&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V+q_n \right) &<&μ^*\Bigl([-1,2) \Bigr) \\ \\ μ^*\Bigl([0,1) \Bigr)&<&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) &<&μ^*\Bigl([-1,2) \Bigr) \end{array}
このような範囲にある、とできるので
\begin{array}{llllll} \displaystyle 1&<&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) &<&3 \end{array}
間違いなくこうなるんですが
「同じ値 μ^*(V) が無限に加算される」以上
\begin{array}{llllll} \displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right)&=&μ^*(V)+μ^*(V)+\cdots \end{array}
\begin{array}{llllll} \displaystyle μ^*(V) =0 &→&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right)=0 \\ \\ μ^*(V)≠0 &→&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right)=\infty \end{array}
こうなるはずなのに
\begin{array}{llllll} \displaystyle 1&<&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) &<&3 \end{array}
この範囲にある
というのは明らかな矛盾です。
\begin{array}{llllll} \displaystyle 1&<&\displaystyle μ^* \left( \bigcup_{n=1}^{\infty} V \right) &<&3 \end{array}
\begin{array}{llllll} \displaystyle μ^*(V)& \not\in &R \end{array}
この条件を満たす実数は存在しません。
まとめると
「完全加法性」を仮定する場合
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty} V+q_n \end{array}
矛盾が出るため
このパターンでは完全加法性を満たしません。
補足しておくと
この結果は「選択公理」を認める場合に限るので
\begin{array}{llllll} \displaystyle \{0\},\{1\},\{2\},\cdots&∈&G&⊂&2^N \end{array}
↓
\begin{array}{llllll} N&=& \displaystyle \{0,1,2,3,4,5,\cdots \} \end{array}
この範囲を制限した
「従属選択公理」などを採用する場合
\begin{array}{llllll} \displaystyle V&=&\{ [r]∈r+Q \mid r+Q ∈R/Q \} \end{array}
「ヴィタリ集合の存在」は保証できず
「ルベーグ外測度」は「完全加法性」を持ちます。
可測関数 Measurable Function
|| 可測空間を繋ぐ感じの関数
可測空間の構造が破綻しない関数
\begin{array}{llllll} \displaystyle (X,σ_X)&→&(Y,σ_Y) \end{array}
\begin{array}{llllll} \displaystyle f&:&X&\to&Y \end{array}
\begin{array}{cclllllll} D&∈&σ_Y &&\to&& f^{-1}(D)&∈&σ_X \end{array}
まあ要は「普通の関数」のことで
だいたいはこの関数に含まれます。
補足しておくと
\begin{array}{llllll} \displaystyle D&∈&σ_Y &&\to&& f^{-1}(D)&∈&σ_X \end{array}
ちょっと記号があれですが
これは要は「両側が可測」ってことなので
定義自体はほんとにそのままです。
それと X,Y ですが
これはだいたい実数 R,R^2 が来ます。
(その場合はボレル集合族上で定義される)
可測関数の具体例
可測空間 (S,σ) 上の話とすると
当然ですが、だいたいの関数は可測関数です。
\begin{array}{llllll} \displaystyle f(x)&=&ax+b \\ \\ f(x)&=&ax^2 \\ \\ f(x)&=&\sin x \end{array}
「連続関数」は「区間→区間」の関数で
\begin{array}{llllll} \displaystyle 2x&:&1&\to&2 \\ \\ \displaystyle \frac{1}{2}x&:&1&←&2 \end{array}
「逆関数」はただ逆を辿るだけなので
もちろん可測関数ですし
\begin{array}{llllll} A&⊂&X \\ \\ \displaystyle A&∈&σ \end{array}
\begin{array}{llllll} \displaystyle 1_A(x)&=&\displaystyle \left\{ \begin{array}{clllll} \displaystyle 1 &&x \in A \\ \\ 0 &&x \not\in A \end{array} \right. \end{array}
定義関数にしても
\begin{array}{llllll} \displaystyle 1_A^{-1}(1)&→&A \\ \\ 1_A^{-1}(0)&→&A^c \end{array}
\begin{array}{llllll} \displaystyle A&∈&σ \\ \\ A^c&\in&σ \end{array}
逆関数は基本辿るだけなので
これも可測関数になります。
それと詳細は省きますが
\begin{array}{cllllll} \displaystyle f+g \\ \\ fg \\ \\ αf &&α∈R \\ \\ |f|^α &&α∈R \end{array}
可測関数にこういった操作を加えても
これらは可測関数になります。
非可測関数の例
「非可測な関数」を作るのは
「ルベーグ非可測な集合」を前提とすれば
\begin{array}{llllll} \displaystyle 1_V(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈V \\ \\ 0&&x∉V \end{array} \right. \end{array}
簡単に生成できます。
(ヴィタリ集合は別記事)
性質やらなんやら
そういったものについては意外と長くなるので
詳しい話は別の記事にまとめておきます。
