|| 基本的な数のこと
「 0,1,π,i,e 」とかのこと。
スポンサーリンク
目次
・一 1 「本質的には『在る』という感じ」
・零 0 「これは『無い』という感じ」
・円周率 π 「円から生まれた子」
・虚数単位 i 「高次方程式から生まれた子」
・ネイピア数 e 「指数関数と微分の子」
数学で扱われる
「基本的な数」と言えば
\begin{array}{ccccc} \displaystyle 1 &&\mathrm{Exist}&\mathrm{Unit} \\ \\ 0 &&\mathrm{No} &\mathrm{Origin} \\ \\ π&&\mathrm{Circle} &\mathrm{Cycle} \\ \\ e&&\mathrm{Differential} &\mathrm{Constant} \\ \\ i&& \mathrm{Rotate}& \mathrm{Outside} \end{array}
まあだいたいこれでしょう。
数Ⅲとかまで触れたことがある人にとっては
どれも馴染み深いものだと思います。
ただこれ、そもそもなんなんでしょ?
なんか分かる気はしますけど
よくよく考えるとよく分からんですよね。
0,1 はかなり直観的
円周率 π もまあ割と直観的ですが
ネイピア数 e
虚数単位 i
この辺りになってくるとちょっと怪しいです。
これらは役割ははっきりしてますけど
具体的に何のことを指してるのかはさっぱり。
とまあそんな感じだと思うので
ちょっとだけ詳しく解説してみました。
(詳細は長くなるので別の記事にまとめてます)
一 \mathrm{One} \,\, 1
|| 最も直観的で原始的ではっきりしてる数
この数は『基準』と捉えるのが直感的です。
\begin{array}{llllll} \displaystyle 1 & \mathrm{Unit} & \mathrm{Exist} \end{array}
これは本質的には『存在』を意味します。
1 の役割
そもそもまず「在る」ことが分からないと
『複数』が生まれることはありません。
\begin{array}{llllll} \displaystyle 1個 &1回 \\ \\ 1\mathrm{s} &1\mathrm{m} &1\mathrm{kg} \end{array}
あらゆる量的概念は
「 1 という基準」が定まって
初めて『比較』が可能になります。
2 も 1000 も
基準となる 1 が定まらなければ
なにを意味しているのか分かりません。
零 \mathrm{Zero} \,\, 0
|| 何も無い・始まりを意味するもの
『無・起点・根源』を意味する数
\begin{array}{llllll} \displaystyle 0&\mathrm{No}&\mathrm{Origin} \end{array}
「 1 」が『直感的な基準』だとするなら
「 0 」は『本質的な基準』です。
ちなみに歴史的には
「ブラーマグプタ」というインドの数学者が
最初に数学的な演算として定義したとされています。
無の存在
これは主に『計算で不都合が生じるから』必要
という感じで存在していて
\begin{array}{llllll} \displaystyle 1個 \\ \\ 1個-1個&=&0個 \end{array}
「 1 の存在」から
『存在が無い』として間接的に導かれます。
単体で意味を持つことはありません。
実数直線にしても
「左右」があって初めて原点は意味を持ちます。
単体の点 O それ自体には特に意味はありません。
0 が無かった時代
この 0 なんですが
実は無かったとしても
そんなに問題無かったりします。
\begin{array}{llllll} \displaystyle \mathrm{I}&\mathrm{I}\hspace{-1.2pt}\mathrm{I}&\mathrm{I}\hspace{-1.2pt}\mathrm{I}\hspace{-1.2pt}\mathrm{I}&\mathrm{I}\hspace{-1.2pt}\mathrm{V}&\mathrm{V}&\mathrm{V}\hspace{-1.2pt}\mathrm{I} \end{array}
というのも
大昔の古代文明やらなにやら
いろんな遺跡、巨大建築物
高度文明を含む文明的なものも含めて
いろんな人の営みがあったわけですが
実はその中に 0 は無かったんです。
いや、厳密にはあったんですが
今のように広く知られた概念ではなく
厳密に定義されたものではありませんでした。
でも、社会は特に問題なく機能した。
それは厳然たる事実で
否定することは決してできません。
0 が否定された時代
現代人である我々にとって
0 はありふれた存在・常識です。
\begin{array}{llllll} \displaystyle 0&&\mathrm{No} &\mathrm{Basis} \end{array}
でもそれは
今を生きる私たちにとっての価値基準
「昔の人間」からしてみれば
0 の存在は常識ではありません。
地動説や地球が丸いといった
そういった話と同列のものでした。
なにより、当時を生きる人たちにとって
それは特に必要なものではなく
それ故か
古代の偉人「アルキメデス」「アリストテレス」
大昔の先駆者と言えば
だいたいこの人たちの名前が出てくると思いますが
実はこの人たち
「 0 の存在」を認めなかったんです。
偉大な先駆者であり
間違いなく優れた頭脳を持っていたはずの彼らが
\begin{array}{llllll} \displaystyle 1円-1円&=&0円 \end{array}
現代人にとってみれば
「疑う余地の無い常識」を否定したんですよ。
まあ彼らも人間です。
アインシュタインも正しい自説を否定したように
時に間違えるのは当然なんですが
『 0 の存在を認めなかった』
これは現代を生きる我々から見れば酷く滑稽な疑問
\begin{array}{llllll} \displaystyle 1+1&=&2 \\ \\ 1-1&=&0 \end{array}
↑ を否定するような暴挙ですが
それでも否定された。
なんなら宗教的にも弾圧された。
それほどまでに
この 0 という概念は否定された過去を持っています。
(我々人類の黒歴史の一つです)
0 の役割
現代人である我々にとって
『 0 が無い』というのは不便極まりないです。
というのも
例えば「時計から 0 が消える」としたら
デジタル表記だとかなり見辛いと思います。
\begin{array}{llllll} \displaystyle 23:59&&\to&&? \end{array}
お金から「 0 が消える」のも分かり難いです。
「引き算で 0 が使えない」のは非常に面倒。
とまあこんな感じで
いくらでも欲しい理由は見つかります。
それくらい
現代人である我々にとって
『 0 の存在』というのは明らかです。
数学的に見た 0
数学的に見ても
もちろん『 0 の存在』は不可欠です。
\begin{array}{llcllll} \displaystyle 0&:=&\{\} \\ \\ &=&∅ \end{array}
自然数を「集合論的に」定義する時
初期値としてあまりにも都合が良いですし
\begin{array}{llllll} \displaystyle 1-1&=&? \end{array}
単純な話、これが定義できないのは不自然
また実数直線においても
0 が無いと超不便です。
円周率 \mathrm{Pi} \,\, π \,\, τ
|| 円から生まれた円のための数
『円を考えるための数』のこと
\begin{array}{cllllll} \displaystyle π\times 2r &=&円周 &&\mathrm{Major} \\ \\ τ\times r &=&円周 &&\mathrm{Minor} \end{array}
「円の半径」を r とすると
「円周率 π,τ 」はこのように定義されています。
より直感的な円周率
円については
そのほとんどが「半径 r 」で定義されているのに
\begin{array}{rllllll} \displaystyle 2πr &=&円周 \\ \\ τr&=&円周 \end{array}
なぜかこれは「直径 2r 」で定義されています。
\begin{array}{llllll} \displaystyle τr&=&円周 \end{array}
ここで生じる尤も過ぎる疑問
それ「半径」で定義すべきじゃね?
そんな疑問から生まれたのが τ で
\begin{array}{llllll} \displaystyle 2π&\to& τ &&1 \, \mathrm{Cycle} \\ \\ 2πr &\to&τr &&\mathrm{Length} \\ \\ πr^2 &\to&\displaystyle \frac{1}{2}τr^2 && \mathrm{Area} \end{array}
これを使うと
いろいろな式がより直感的に。
\begin{array}{llllll} \displaystyle \sin τ &=&\sin 0 \\ \\ \cos τ &=&\cos 0 \end{array}
\begin{array}{llllll} \displaystyle π \,\mathrm{radian}&=&180° \\ \\ τ \,\mathrm{radian} &=&360° \end{array}
いろいろと正常になります。
マーダヴァ-ライプニッツ級数
近似値の計算には
『ライプニッツ級数』というのがよく使われます。
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n \to \infty}\sum_{k=0}^{n}\frac{(-1)^k}{2k+1} &=&\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots \\ \\ &=&\displaystyle\frac{π}{4} \end{array}
これ発見した人ほんとすごいです。
式だけ見てもまじで意味が分かりません。
(詳細はちょっと長くなるので別記事で)
ちなみに発見したのは
「マーダヴァ(最初)」さんと
「ライプニッツ( 300 年後)」さんです。
虚数単位 \mathrm{Imaginary \,\, Unit} \,\, i
|| 二次方程式の一般解を説明するもの
『高次方程式の解の説明のための数』
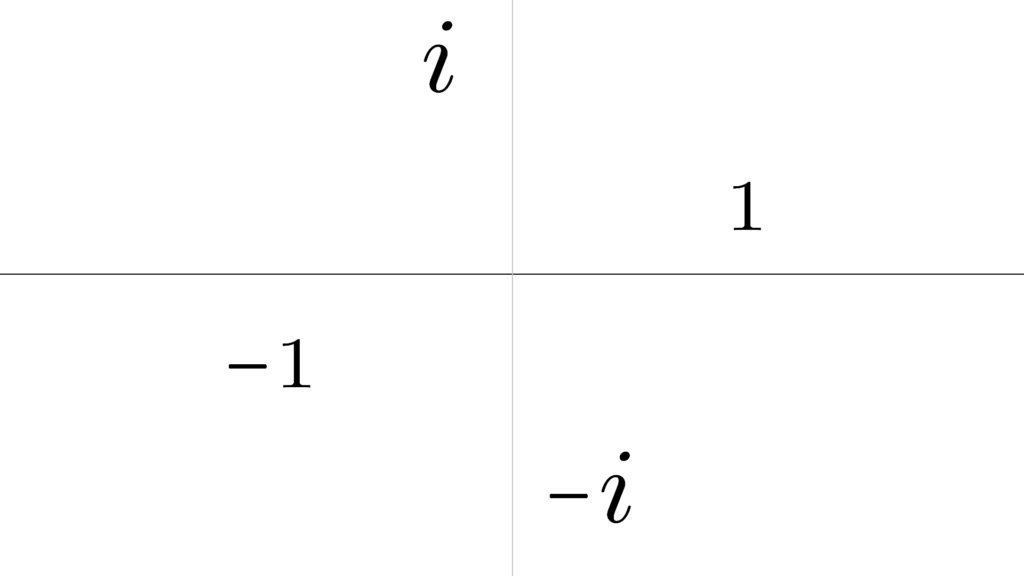
平面的には 90° の回転を意味します。
\begin{array}{lcrrrrrrllll} \displaystyle i^0 &=&1 &&&0° \\ \\ i^1 &=&i &&&90° \\ \\ i^2 &=&-1 &&&180° \\ \\ i^3 &=&-i &&&270° \\ \\ i^4 &=&1 &&&360° \end{array}
4 回掛けると元通りなため
複素数 Complex Number
|| 虚数の存在を認めた世界
「虚数があること前提」の数全体のこと
\begin{array}{llllll} \displaystyle z&=&a+bi \\ \\ z&=&r\Bigl( \cos θ +i\sin θ \Bigr) \\ \\ &=&\displaystyle\sqrt{a^2+b^2}\left( \frac{a}{\sqrt{a^2+b^2}}+i\frac{b}{\sqrt{a^2+b^2}} \right) \end{array}
数式的には
a,b を実数として
こんな感じで表現されます。
\begin{array}{llllll} \displaystyle x^2&=&i \end{array}
なのでこのような計算を考える時
\begin{array}{ccrccccllllll} \displaystyle x&=&\pm \sqrt{i} &&△ \\ \\ (a+bi)^2&=&i &&〇 \end{array}
この形を考慮しなければなりません。
\begin{array}{llllll} \displaystyle (a+bi)^2&=&a^2+2a(ib)+(ib)^2 \\ \\ &=&a^2+2abi -b^2 \\ \\ &=&a^2-b^2+2abi \end{array}
\begin{array}{llllll} \displaystyle i&=&0+1i \end{array}
\begin{array}{cllllll} \displaystyle a^2-b^2&=&0 \\ \\ 2ab&=&1 \end{array}
\begin{array}{lcllllll} \displaystyle a^2-b^2&=&(a+b)(a-b) \\ \\ &=&0 \end{array}
\begin{array}{llllll} \displaystyle a&=&\pm b \end{array}
\begin{array}{rccllllll} \displaystyle 2ab&=&1 \end{array}
\begin{array}{llllll} a=b&&\displaystyle \left( \begin{array}{rccllllll} \displaystyle 2(+ b)b&=&1 \\ \\ b^2&=&\displaystyle\frac{1}{2} \\ \\ b&=&\displaystyle\pm\sqrt{\frac{1}{2}} \end{array} \right) \\ \\ \\ a=-b&&\displaystyle \left( \begin{array}{rccllllll} \displaystyle 2(- b)b&=&1 \\ \\ -b^2&=&\displaystyle\frac{1}{2} \\ \\ b&=&\displaystyle\pm\sqrt{\frac{-1}{2}} \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle a,b&∈&R \end{array}
\begin{array}{llllll} \displaystyle a&=&b \\ \\ &&b&=&\displaystyle\pm\sqrt{\frac{1}{2}} \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{rlllll} \displaystyle \sqrt{i} \\ \\ -\sqrt{i} \end{array} \right) &=& \displaystyle \left( \begin{array}{rllllll} \displaystyle \sqrt{\frac{1}{2}}+\sqrt{\frac{1}{2}}i \\ \\ \displaystyle -\sqrt{\frac{1}{2}}-\sqrt{\frac{1}{2}}i \end{array} \right) \end{array}
ちなみに答えはこんな感じ。
( 45° 回転になってます)
ネイピア数 \mathrm{Napier's \,\, Number} \,\, e
|| 指数関数と微分を単純にしたくて
『微分の単位としての数』
\begin{array}{ccclll} \displaystyle \lim_{n\to \infty} &\displaystyle \left(1+ \frac{1}{n} \right)^n&=&e \\ \\ \displaystyle \lim_{h\to 0} &\displaystyle\frac{e^h-1}{h}&=&1 \end{array}
これの説明は長くなるので
詳細は別の記事にまとめておきます。
