|| 測るってそもそもなに?って感じの話
メイントピックは『長さ』『面積』『体積』
スポンサーリンク
「測度」というのは
『長さ』『面積』『体積』の総称になります。
目次
測度「長さとか面積とか体積とかのこと」
数え上げ測度「要素の個数を返すやつ」
ジョルダン測度「集合と図形の定義」
点の測度「もちろん 0 」
有理数の測度「ぎっしりだけど 0 」
区間の測度「閉区間も開区間も同じ」
完全加法族「測度を矛盾なく導ける枠組み」
可測空間「完全加法族を前提とするやつ」
可測関数「可測空間の構造が破綻しない関数」
測度空間「測度を厳密に定義するための前提」
定義関数「条件を満たす場合に 1 を返す関数」
ディラック測度「定義関数から導かれる測度」
完備測度「後で点を追加できる感じ」
ルベーグ測度「ジョルダンのやつを掘り下げたやつ」
これの発端は
「積分可能の範囲についての疑問」で
\begin{array}{rllll} \displaystyle f(x)&=& \displaystyle \frac{a_0}{2}+\sum_{k=1}^{\infty} a_k\cos kx+b_k\sin kx \\ \\ \\ \displaystyle a_k&=&\displaystyle \frac{1}{π} \int_{-\infty}^{\infty} f(x)\cos kx \,dx \\ \\\displaystyle b_k&=&\displaystyle \frac{1}{π} \int_{-\infty}^{\infty} f(x)\sin kx \,dx \end{array}
具体的には
「フーリエ級数」の適用可能な範囲が
当時『任意の関数 f 』とされていたわけですが
\begin{array}{llllll} \displaystyle f(x)&=& \displaystyle \frac{a_0}{2}+\sum_{k=1}^{\infty} a_k\cos kx+b_k\sin kx \end{array}
この『任意の関数』って部分
かなり怪しいですよね?
\begin{array}{llllll} \displaystyle \displaystyle 1_Q(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈Q \\ \\ 0 &&x∈R\setminus Q \end{array} \right. \end{array}
実際、リーマン積分できないものはあって
これは覆しようのない事実ですから
「積分」という操作は
明らかに「任意の関数」では行えません。
とまあこのような経緯があり
この疑問を解消するために生まれたのが
「測度」という概念で
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle S&=&A\sqcup B \\ \\ |S|&=&|A\sqcup B| \end{array} \right) &\to&|S|=|A|+|B| \end{array}
それを研究し
矛盾を解消した分野が『測度論』
そしてほぼ全ての範囲で積分可能なやり方が
『ルベーグ積分』になります。
まあつまり『測度論』のおかげで
きちんと「面積」とかが使える感じです。
補足しておくと
特に制限が無い場合
\begin{array}{llllll} \displaystyle 1&=&2 \end{array}
という定理が導かれます。
非交和 Disjoint Union
この記事では ↑ 以外で使いませんが
\begin{array}{cccccccccc} \displaystyle \left( \begin{array}{cccllllll} \displaystyle A∩B&=&∅ \\ \\ U\setminus A&=&B \end{array} \right) &&←&& A \sqcup B&=&U \end{array}
この記号 \sqcup の意味はこうです。
わりと見るので念のため紹介しておきます。
測度 Measure
|| 測れる量を表す数値
『長さ』『面積』『体積』とかのこと
\begin{array}{llllll} \displaystyle μ&:&S &\to&[0,\infty)∪\{\infty\} \end{array}
\begin{array}{llrllll} \displaystyle m(S) &&μ(S) \end{array}
厳密には「 ↑ の値を返す関数」のことで
『 μ(S) 』みたいに書かれたりします。
ジョルダン測度 Jordan Measure
|| 図形の集合での直感的な定義
「区間」と「直積」で表現します。
\begin{array}{ccccccc} \displaystyle [a,b)×[c,d)&\to&(b-a)\times (d-c) \\ \\ [0,1)×[0,1)&\to&1\times 1 \end{array}
\begin{array}{llllll} \displaystyle μ \Bigl( [a,b)×[c,d)\Bigr)&=&(b-a)\times (d-c) \end{array}
例えば「面積」ならこう
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b)\Bigr)&=&(b-a) \end{array}
1次元の「長さ」ならこうなります。
(ルベーグ測度でももちろんこうなる)
より複雑な図形
↑ のやり方だけでは
「長方形の面積」しか表現できませんが
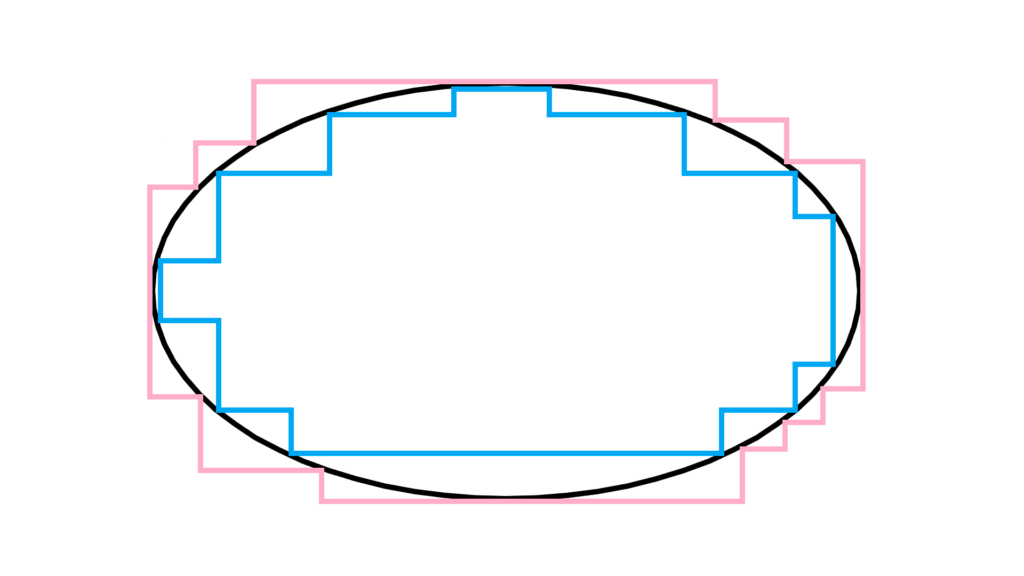
これを応用すれば
あらゆる図形の面積・測度が表現可能で
(限界はあるんですが)
\begin{array}{llllll} \displaystyle && S &⊂&S_{\mathrm{out}} \\ \\ S_{\mathrm{in}}&⊂& S \end{array}
\begin{array}{rccllllll} \displaystyle μ_{\mathrm{in}}(S)&=&\sup(μ(S_{\mathrm{in}})) \\ \\ μ_{\mathrm{out}}(S)&=&\inf(μ(S_{\mathrm{out}})) \end{array}
「外測度 μ_{\mathrm{out}} (赤線で囲われた部分の測度)」
「内測度 μ_{\mathrm{in}} (青線で囲われた部分の測度)」
なんていう概念を使えば
\begin{array}{llllll} \displaystyle μ_{\mathrm{in}}(S) &=&μ_{\mathrm{Answer}}(S) &=&μ_{\mathrm{out}}(S)\end{array}
「積分」のように
「上限・下限」から
間接的に測度を求めることができます。
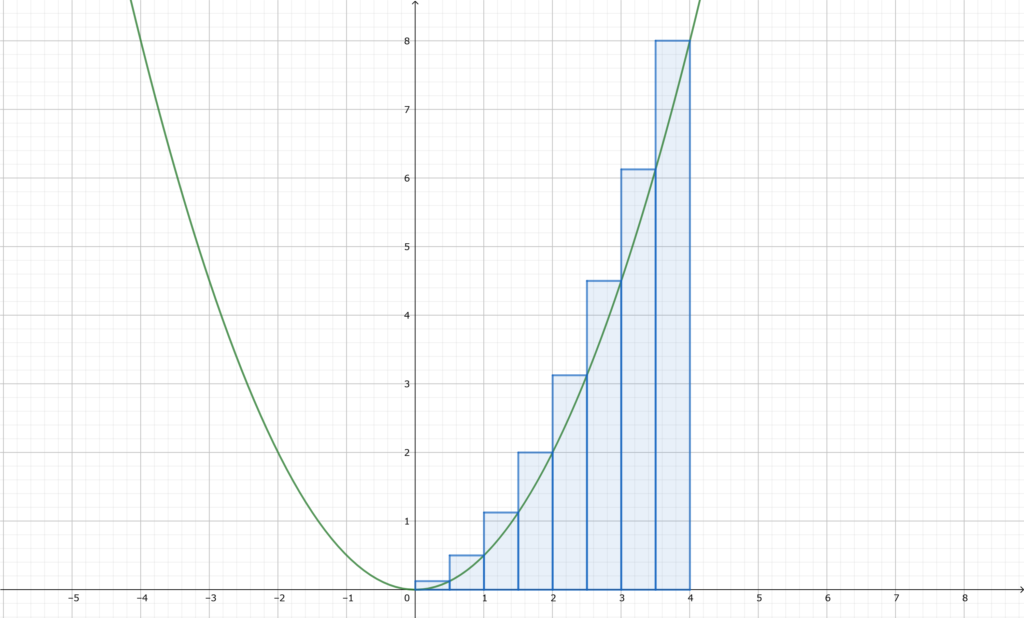
これはこの考え方をそのまま使った感じです。
(リーマン積分の計算)
点と外測度
測度 μ(X) が定義上 0 以上であることから
「測度が 0 になる集合」と「外測度」を用いると
\begin{array}{llllll} \displaystyle 0&≤& μ(A) &≤&μ(X) \end{array}
このように
「測度が 0 になる図形」を求めることができます。
その中でも
特に代表的な問題が「点の測度」で
\begin{array}{llllll} \displaystyle \{r\} &&1 \,\, \mathrm{Point} \\ \\ [r,r+ε) &&\mathrm{Interval} \end{array}
「点の大きさ」は 0 であって欲しい
これは当然の要請ですから
\begin{array}{llllll} \displaystyle \{r\}&⊂&[r,r+ε) \end{array}
それを確認するため
このように区間を定めると
\begin{array}{llllll} \displaystyle μ\Bigl( [r,r+ε) \Bigr)&=&(r+ε)-r \\ \\ &=&ε \end{array}
「外測度 μ\Bigl( [r,r+ε) \Bigr) 」から
\begin{array}{llllll} \displaystyle 0&≤& μ\Bigl( \{r\}\Bigr) &≤&μ\Bigl([r,r+ε) \Bigr) \\ \\ \displaystyle 0&≤& μ\Bigl( \{r\}\Bigr) &≤&ε \end{array}
このような関係が得られて
\begin{array}{llllll} \displaystyle \displaystyle && 0&≤& μ\Bigl( \{r\}\Bigr) &≤&ε \\ \\ \displaystyle -ε_0&<&0&≤& μ\Bigl( \{r\}\Bigr) &≤&ε&<&ε_0 \end{array}
\begin{array}{llllll} \displaystyle \left| μ\Bigl( \{r\}\Bigr)-0 \right|&<&ε_0 \end{array}
「収束」の定義から
「点の測度」が 0 になることが確かめられます。
有理数と外測度
「点の測度」と
「自然数との全単射の存在」から
\begin{array}{llllll} \displaystyle Q&=&\{q_0\}∪\{q_1\}∪\{q_2\}∪\cdots \\ \\ &=&\displaystyle \bigcup_{n=0}^{\infty}\{q_n\} \end{array}
有理数はこのように表現できるので
\begin{array}{llllll} \displaystyle μ \Bigl( \{q_0\}∪\{q_1\}∪\cdots \Bigr)&=&\displaystyle μ \Bigl( \{q_0\} \Bigr) +μ \Bigl( \{q_1\} \Bigr)+\cdots \\ \\ &=&0+0+0+\cdots \\ \\ &=&0 \end{array}
そのままこうなりそうですが
「ジョルダン測度」では
「ジョルダン外測度・内測度」から
\begin{array}{llllll} \displaystyle Q_{[0,1)}&=&Q∩[0,1) \end{array}
\begin{array}{llllll} \displaystyle μ_{\mathrm{in}}(Q_{[0,1)})&=&μ(∅) &=&0 \\ \\ μ_{\mathrm{out}}(Q_{[0,1)})&=&μ([0,1)) &=&1 \end{array}
このように答えを求める必要があるので
\begin{array}{llllll} \displaystyle μ_{\mathrm{in}}(Q_{[0,1)})&≠&μ_{\mathrm{out}}(Q_{[0,1)}) \end{array}
これは「ジョルダン測度」では
大きさを測れない集合になります。
(ルベーグ測度だといけてちゃんと 0 になる)
開区間と閉区間と外測度
ジョルダン測度は半開区間で定義されていて
開区間と閉区間がどうなるか分かりませんが
\begin{array}{llllll} \displaystyle μ\Bigl( (a,b) \Bigr)&=&μ\Bigl( [a,b) \Bigr) &=&μ\Bigl( [a,b] \Bigr) \end{array}
結果はこうなります。
これは「外測度・内測度」を使うと明らかで
\begin{array}{rccll} \displaystyle [a+ε,b)&⊂& (a,b) &⊂& [a,b) \\ \\ [a,b) &⊂&[a,b]&⊂&[a,b+ε) \end{array}
この関係から
\begin{array}{ccccccc} μ\Bigl( [a+ε,b) \Bigr)&≤&\displaystyle μ\Bigl( (a,b) \Bigr)&≤&μ\Bigl( [a,b) \Bigr) \\ \\ -ε+b-a&≤&μ\Bigl( (a,b) \Bigr)&≤&b-a \\ \\ \\ μ\Bigl( [a,b) \Bigr)&≤&\displaystyle μ\Bigl( [a,b] \Bigr)&≤&μ\Bigl( [a,b+ε) \Bigr) \\ \\ b-a&≤&μ\Bigl( [a,b] \Bigr)&≤&b-a+ε \end{array}
直ちに導かれます。
これは「点の測度」から
\begin{array}{ccc} \displaystyle [a,b]&=&[a,b)∪\{b\} \\ \\ \\ \displaystyle μ\Bigl( [a,b] \Bigr)&=& μ\Bigl( [a,b)∪\{b\} \Bigr) \\ \\ &=&\displaystyle μ\Bigl( [a,b) \Bigr)+μ\Bigl( \{b\} \Bigr) \\ \\ &=&b-a+0 \end{array}
単にこうしてもOK
これを見て分かると思いますが
半開区間で定義されているのは
\begin{array}{llllll} \displaystyle (a,b) &⊂& [a,b) &⊂&[a,b] \end{array}
「半開区間の測度」が
「外測度・内測度」の役割を果たすからです。
測度に求められる基本的な性質
『長さ』とか『面積』とか
その辺りが持ってる性質を
当然ですが「測度」は求められてます。
\begin{array}{llllll} \displaystyle μ(S)&∈&R∪\{\infty\} \end{array}
\begin{array}{llllll} \displaystyle μ(∅)&=&0 \\ \\ \displaystyle μ\Bigl([0,1]\times [0,1] \Bigr)&=&1 \end{array}
\begin{array}{llllll} \displaystyle μ(A∪B)&=&μ(A)+μ(B) \end{array}
具体的には
こういうのを測度はできて欲しい感じで
定義はこれらを実現するためのものになります。
ちなみに
「有理数」の測度のような
\begin{array}{llllll} \displaystyle μ(N)&=&0 \\ \\ μ(Q)&=&0 \end{array}
「測度が 0 になる集合」は
そのまま「零集合」と呼ばれることがあります。
少し厳密な測度の定義
「初期値」と「性質」で定義されています。
\begin{array}{llllll} \displaystyle μ(∅)&=&0 \end{array}
\begin{array}{llllll} \displaystyle\left(\begin{array}{rllllll} i&≠&j \\ \\ \displaystyle A_i∩A_j&=&∅ \end{array} \right) &\to&\displaystyle\left( \begin{array}{llllll} \displaystyle μ\left(\bigcup_{i∈N} A_i\right)=\displaystyle\sum_{i∈N} μ(A_i) \end{array}\right) \end{array}
初期値については
「空集合なら測度は 0 」
性質については
「重なってないなら足せる」って感じです。
\begin{array}{rclllllll} \displaystyle μ(A∪B)&=&μ(A)+μ(B) \\ \\ &↓ \\ \\ \displaystyle μ\Bigl( A∪(B∪C) \Bigr)&=&μ(A)+μ(B∪C) \\ \\ &=&μ(A)+μ(B)+μ(C) \end{array}
個数を減らして最低限にした
\begin{array}{llllll} \displaystyle μ(A∪B)&=&μ(A)+μ(B) \end{array}
こっちの性質も満たします。
\begin{array}{rllllll} i≠j &\to& \displaystyle A_i∩A_j=∅ \end{array}
ちなみにこの性質には
「互いに素」なんて名前が付いてます。
数え上げ測度 Counting Measure
|| 確率とかで見る測度
測度を意識するのは
だいたい「面積」の話でなんですが
\begin{array}{llllll} \displaystyle μ(S)&=&|S| \end{array}
実は「個数」も測度の一種だったりします。
(確率を扱う時に使われる)
これはそのまま
単に要素数を抜き出すだけなので
特に語ることは無いですね。
ただ「測度にはいろんな種類がある」
この事実を実感する上では非常に重要になります。
完全加法族 Completely Additive
|| ちゃんと足し算ができる集合のこと
『測度』を定義できる族 σ のこと
(族は集合を要素に持つ集合のこと)
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
最低限の定義はこんな感じで
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ S∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A,B∈σ&\to&\displaystyle A\setminus B∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n ∈σ \end{array} \right) \end{array}
実態はこんな感じです。
これは「足し算」の無矛盾を保証するもので
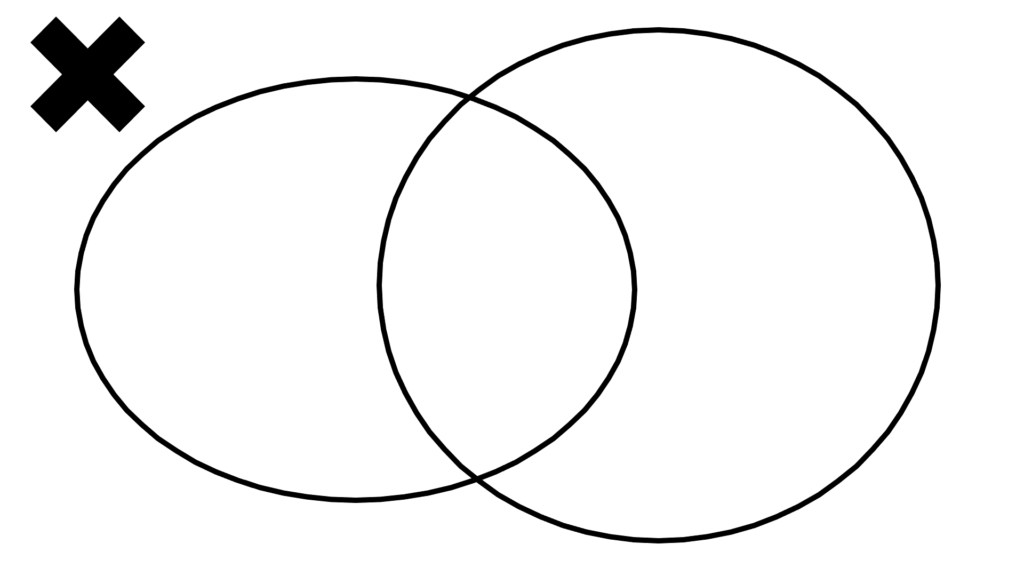
こういうのをNGにしています。
(詳細はちょっと長くなるので別記事で)
可測空間 Measurable Space
|| 完全加法族だよという前提の宣言
集合を完全加法族にする感じ
\begin{array}{llllll} \displaystyle (S,σ) \end{array}
加工されることになる集合 S と
そこから作られる完全加法族 σ のセット
その前提を「可測空間 (S,σ) 」と言います。
\begin{array}{llllll} \displaystyle R&\to&∅,I_1,\cdots,R \\ \\ R^2&\to&∅,I_{11}\times I_{12},\cdots,R^2 \end{array}
だいたい加工されるのは「実数」
加法族は「その区間・領域の集合」になります。
可測関数 Measurable Function
|| 可測空間を繋ぐ感じの関数
可測空間の構造が破綻しない関数
\begin{array}{llllll} \displaystyle (X,σ_X)&→&(Y,σ_Y) \end{array}
\begin{array}{llllll} \displaystyle f&:&X&\to&Y \end{array}
\begin{array}{llllll} \displaystyle D&∈&σ_Y &&\to&& f^{-1}(D)&∈&σ_X \end{array}
まあ要は「普通の関数」のことで
だいたいはこの関数に含まれます。
(これの詳細は長くなるので別記事で)
非可測関数の例
「非可測な関数」を作るのは簡単ですが
「ルベーグ非可測な集合」が必要で
\begin{array}{llllll} \displaystyle 1_V(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈V \\ \\ 0&&x∉V \end{array} \right. \end{array}
この「ルベーグ非可測集合 V 」は
生成がちょっと大変だったりします。
(ヴィタリ集合が代表的 詳細は別記事)
他にもやり方はありますが
非可測というとだいたいこいつのことを指します。
測度空間 Measure Space
|| 測度を厳密に定義するための前提
「可測空間」上で定義されるやつ
\begin{array}{llllll} \displaystyle (S,σ,μ) \end{array}
「測度」を厳密に定義するためのものですが
「可測空間」に「測度」を付け足しただけです。
根本的に
ただ『普通のことができる』と言ってるだけなので
「可測空間」が分かれば特に問題なく分かると思います。
\begin{array}{llllll} \displaystyle A∈σ &\to& μ(A)=r \end{array}
ちなみにこの時の集合 A には
「可測集合」なんて名前がついていたりします。
測度のより厳密な話
よく見る性質なので
「有限加法性」「単調性」「平行移動」
これらの確認はしておきます。
\begin{array}{rllllll} i≠j &\to& \displaystyle A_i∩A_j=∅ \end{array}
\begin{array}{llllll} \displaystyle μ\left( \bigcup_{k=1}^{n}A_k \right)&=&\displaystyle\sum_{k=1}^{n}μ(A_k) \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle A⊂B \\ \\ μ(A)<\infty \end{array} \right) &\to& \displaystyle \left( \begin{array}{llllll} \displaystyle μ(A)≤μ(B) \\ \\ μ(B\setminus A)=μ(B)-μ(A) \end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle μ(A)&=&μ(A+x) \end{array}
数式的にはこんな感じ。
(もちろん他にもいろいろあります)
有限加法性
2つ以上の図形の足し算ができる
\begin{array}{rllllll} i≠j &\to& \displaystyle A_i∩A_j=∅ \end{array}
\begin{array}{llllll} \displaystyle μ\left( \bigcup_{k=1}^{n}A_k \right)&=&\displaystyle\sum_{k=1}^{n}μ(A_k) \end{array}
当たり前すぎますが
これについてちゃんと確認をしておきます。
\begin{array}{llllll} \displaystyle μ(A∪B)&=&μ(A)+μ(B) \end{array}
といってもまあこれはほぼ説明不要でしょう。
\begin{array}{llllll} \displaystyle A_n&=&A_{n+1}&=&\cdots&=&A_{n+m}&=&\cdots \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{m=0}^{\infty}A_{n+m}&=&A_n \end{array}
ちょっとした工夫は必要ですが
\begin{array}{llllll} \displaystyle μ\left( \bigcup_{k=1}^{\infty}A_k \right)&=&\displaystyle\sum_{k=1}^{\infty}μ(A_k) \end{array}
↓
\begin{array}{llllll} \displaystyle μ\left( \bigcup_{k=1}^{n}A_k \right)&=&\displaystyle\sum_{k=1}^{n}μ(A_k) \end{array}
測度の定義から直ちに導かれます。
単調性
これに関してもまあ見たままですね。
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle A⊂B \\ \\ μ(A)<\infty \end{array} \right) &\to& \displaystyle \left( \begin{array}{llllll} \displaystyle μ(A)≤μ(B) \\ \\ μ(B\setminus A)=μ(B)-μ(A) \end{array} \right) \end{array}
μ(A)<\infty 不定形 \infty-\infty の回避を除けば
特に疑問に思う部分は無いと思います。
\begin{array}{llllll} \displaystyle B&=&B\setminus A∪A \\ \\ μ(B)&=&μ(B\setminus A∪A) \\ \\ &&μ(B\setminus A∪A)&=&μ(B\setminus A)+μ(A) \end{array}
\begin{array}{llllll} \displaystyle μ(B\setminus A)&=&μ(B)-μ(A) \end{array}
\begin{array}{llllll} \displaystyle 0&≤&μ(X) \\ \\ 0&≤&μ(B\setminus A) \\ \\ 0&≤&μ(B)-μ(A) \end{array}
\begin{array}{llllll} \displaystyle μ(A)&≤&μ(B) \end{array}
ちょっとした工夫はありますが
証明も集合について知ってればすぐです。
ちなみに補足しておくと
この性質のおかげで「近似」ができます。
\begin{array}{ccccccllllll} \displaystyle A&⊂&X&⊂&B \\ \\ μ(A)&≤&μ(X)&≤&μ(B) \end{array}
この性質がないと積分とかができません。
単調性の一般化
別の記事で詳しくやる「ルベーグ外測度」では
\begin{array}{llllll} \displaystyle μ(B)&=&μ(B\setminus A∪A) \\ \\ &&μ(B\setminus A∪A)&≤&μ(B\setminus A)+μ(A) \end{array}
\begin{array}{llllll} \displaystyle 0&≤&μ(B)-μ(A)&&? \end{array}
「完全加法性」が満たされない場合があるため
この関係は一般的にはこうなるんですけど
(劣加法性とか言われる性質)
\begin{array}{rcrlll} \displaystyle A&⊂&B \\ \\ \inf A&\textcolor{pink}{≥}&\inf B \\ \\ \sup A&\textcolor{skyblue}{≤}&\sup B \end{array}
\begin{array}{lcclcrlllll} \displaystyle [1,2) &&& \inf [1,2)&=&1 \\ \\ [0,3) &&& \inf [0,3)&=&0 \end{array}
A⊂B だと
集合 B は A の要素を全て持つことから
\begin{array}{cccll} μ(A)&≤&μ(B) \\ \\ \displaystyle \sup A -\inf A&≤&\sup B -\inf B \end{array}
確実に集合 A 以上に広い範囲をとるので
\begin{array}{llllll} \displaystyle μ(A)&≤&μ(B) \end{array}
結果、同様の結論が得られます。
平行移動不変性
これは図形の移動の話で
まあ感覚的には明らか
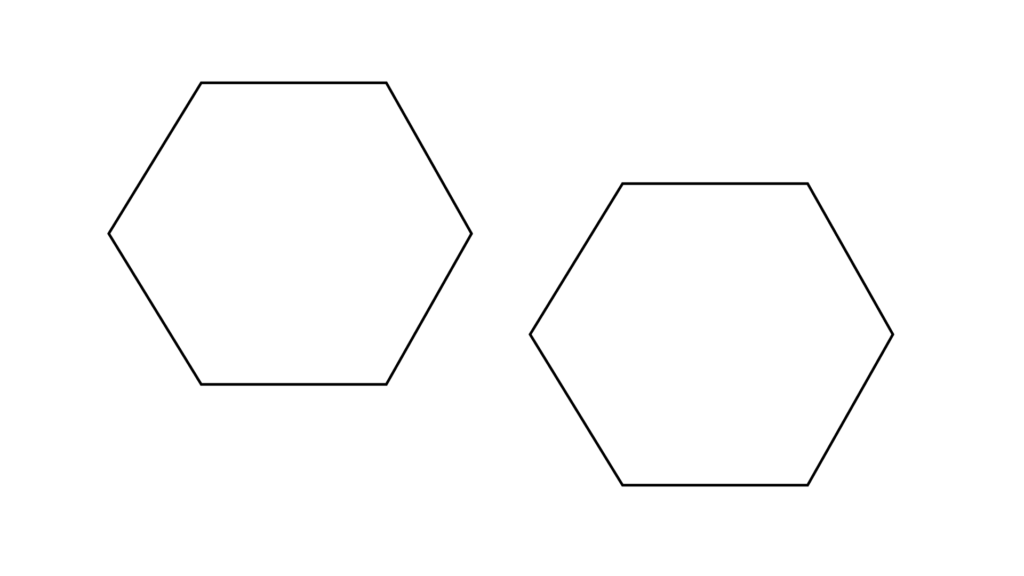
特に疑問の余地はありません。
ただ形式的にはどうなるのか
その辺りはちょっと怪しいと思うので
念のため確認しておきます。
やることは単純
\begin{array}{llllll} \displaystyle [0,1) &&\to&& &&1-0 \\ \\ [0+c,1+c) &&\to&& (1+c)-(0+c) &=& 1-0 \end{array}
これを一般化するだけなので
\begin{array}{llllll} \displaystyle I_n&=&[a_n,b_n) \\ \\ I_n+c&=&[a_n+c,b_n+c) \end{array}
測度を求めたい図形を A
それを平行移動した図形を A+c として
\begin{array}{llllll} \displaystyle A&=&\displaystyle\bigcup_{n=1}^{\infty}I_n \\ \\ A+c&=&\displaystyle\bigcup_{n=1}^{\infty}I_n+c \end{array}
こんな感じに定義すると
\begin{array}{llllll} \displaystyle μ(I_n)&=& && b_n-a_n \\ \\ μ(I_n+c)&=& (b_n-c)-(a_n-c) &=&b_n-a_n \end{array}
こうですから
\begin{array}{llllll}\displaystyle μ\left( \displaystyle\bigcup_{n=1}^{\infty}I_n \right)&=&\displaystyle μ\left( \displaystyle\bigcup_{n=1}^{\infty}I_n+c \right) \\ \\ \displaystyle μ(A)&=&μ(A+c) \end{array}
もちろんこうなるので
これで平行移動による測度の不変性は示せました。
定義関数 Indicator Function
|| 特定の条件に合う時 1 を返す関数
かなり実用的で便利な関数です。
\begin{array}{rcl} \displaystyle 1_D(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∉D \end{array} \right. \\ \\ \\ \displaystyle χ_P(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&P(x)\,\,\mathrm{is} \,\, \mathrm{True} \\ \\ 0 &&P(x) \,\,\mathrm{is} \,\, \mathrm{False} \end{array} \right. \end{array}
1_D と書かれることが多いですが
χ_D と書かれる場合も多いです。
ちなみに「定義関数」には
「指示関数」なんていう別の名前もあります。
(特性関数と呼ばれることもある)
指示関数と測度
定義関数にはいろいろ性質があって
\begin{array}{cccllllll} \displaystyle \int_{-\infty}^{\infty}1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} \,dx \\ \\ \displaystyle \int_{-\infty}^{\infty}f(x)1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} f(x) \,dx \end{array}
その中でも「測度」
特に「積分」を考える場合では
こういう性質を意識することが多いです。
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle f(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
またこの条件からは
\begin{array}{cllllll} \displaystyle a_1 1_{D_1}(x) \\ \\ a_2 1_{D_2}(x) \\ \\ \vdots \\ \\ a_n 1_{D_n}(x) \end{array}
x が決まると a_k 以外は 0 になる
あるいは範囲 D_k 外で 0 になることから
\begin{array}{llllll} \displaystyle f(x)&=&\displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \end{array}
このような表現が導かれ
\begin{array}{llllll} \displaystyle μ \left( \displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \right)&=&\displaystyle μ\Bigl( a_1 1_{D_1}(x)\Bigr) +\cdots + μ\Bigl( a_n 1_{D_n}(x)\Bigr) \end{array}
「加法性」の観点から
これが「ルベーグ積分」に関わってきたりします。
ディラック測度 Dirac Measure
|| ほぼ定義関数の測度
ほぼというか定義関数そのものです。
\begin{array}{llllll} \displaystyle δ_x(D)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∈U\setminus D \end{array} \right. \\ \\ \\ \displaystyle 1_D(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∈U\setminus D \end{array} \right. \end{array}
いろんなところで見る上に実用性があるので
これは覚えておいた方が良いと思います。
完備測度 Complete Measure
|| 確実に極限をとれる(穴が無い)感じ
任意の「零集合 A 」が可測である
(どこにでも点が存在する)
\begin{array}{llllll} μ(N)&=&0 \\ \\ \displaystyle μ(A⊆N)&=&0 \end{array}
\begin{array}{llllll} \displaystyle 0&≤&μ(A)&≤&μ(N) \end{array}
この時の「測度空間」を
「完備測度空間」なんて言ったりします。
(稠密であるとか言ったりもします)
具体的には
\begin{array}{llllll} (R,\mathfrak{B}(R),μ) \end{array}
だいたい「実数」のことです。
完備測度の役割
分かりにくいですが
これはつまり「コーシー列」の話で
\begin{array}{llllll} \displaystyle N≤n,m &&⇒&&|a_n-a_m|<ε \\ \\ n,m \to \infty &&⇒&&\displaystyle |a_n-a_m|\to 0 \end{array}
\begin{array}{llllll} \displaystyle \lim_{n,m\to \infty}|a_n-a_m|&=&0 \end{array}
この操作ができる
だから「収束する」を保証できる
\begin{array}{llllll} \displaystyle 0&≤&μ(A)&≤&μ(N) \end{array}
とまあそんな感じで
\begin{array}{llllll} \displaystyle μ(A)&=&\displaystyle \lim_{n,m\to \infty} \Bigl| μ(A_n)-μ(A_m) \Bigr| \\ \\ &=&\displaystyle \lim_{n,m\to \infty} \Bigl| μ(A_n \setminus A_m) \Bigr| \end{array}
この「零集合 A (点)」を
良い感じに定義できる
みたいなことを完備性は保証しています。
これは「位相」を理解していないと
厳密にはよく分からないと思いますが
とりあえずこの時点では
「収束する」を保証している
\begin{array}{llllll} \displaystyle \lim_{x\to a}f(x)&=&f(a) \end{array}
まあつまり
「極限の操作」を保証している
という感じに理解していればだいたい合ってます。
全部入ってないと完備ではない
分かりやすい例として
\begin{array}{llllll} \displaystyle σ_X&=&\{ ∅,X \} \end{array}
\begin{array}{llllll} \displaystyle μ(X)&=&0 \\ \\ μ(∅)&=&0 \end{array}
例えばこのように
「完全加法族 σ_X 」「測度 μ 」を定義すると
\begin{array}{llllll} \displaystyle I_X&⊂&X \end{array}
\begin{array}{llllll} \displaystyle μ(I_X)&=&0 &&? \end{array}
「 X の部分集合 I_X 」が空集合以外に存在するなら
『全ての零集合』が σ_X に含まれないため
「完備」ではなくなります。
ルベーグ測度 Lebesgue Measure
|| ジョルダン測度を拡張した考え方
全体を分割する感じのやつ
\begin{array}{cccllllll} \displaystyle D&=&[a,b)\times [c,d) \\ \\ μ(D)&=&(b-a)(d-c) \end{array}
\begin{array}{llllll} \displaystyle μ^{*}(D)&=&\displaystyle\inf \left( \lim_{n\to\infty} \sum_{k=1}^{n}μ(D_k) \right) \end{array}
数式的にはこんな感じで
ちょっとややこしいですが
言ってることはシンプル
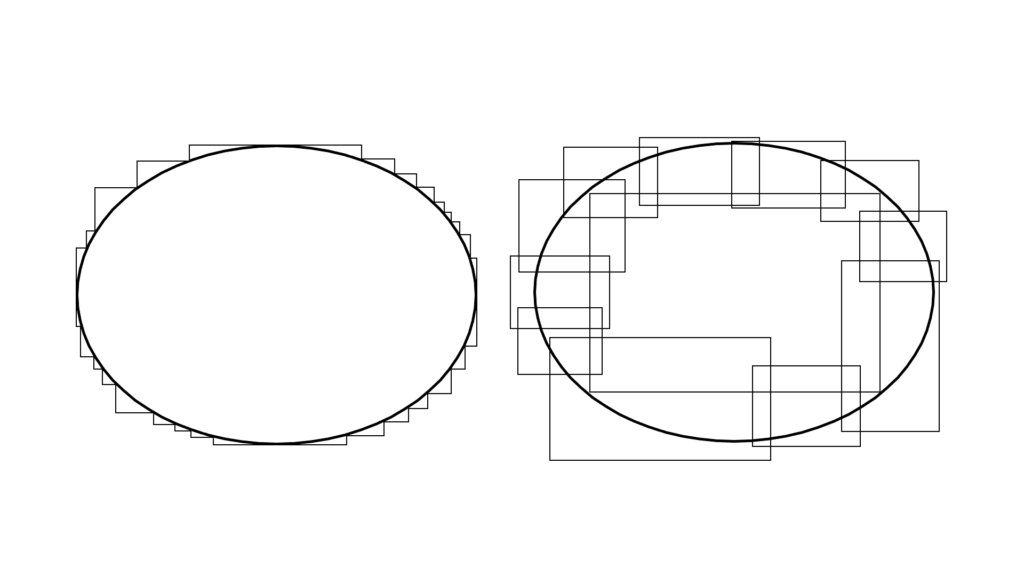
ジョルダン測度と比較するとこんな感じで
ルベーグ測度は小分けにして考えてるだけ。
\begin{array}{llllll} \displaystyle S_{\mathrm{out}}&&\to&& D_1∪D_2∪\cdots ∪D_n ∪\cdots \end{array}
特に疑問の余地は無いと思います。
(長くなるので詳細は別の記事で)
