|| 連続とかを説明するための基礎となる概念
開区間とかを説明できる より厳密な概念
スポンサーリンク
目次
極限「近付けるっていう感覚の形式的表現」
連続「繋がってる感じ」
位相「極限の操作が可能な構造」
開区間「境界を持たない区間のこと」
ユークリッド距離「近さの指標」
近傍「距離を使わない考え方」
開集合「開区間をより厳密に説明する概念」
閉集合「開集合に補集合操作を加えると」
連続写像「連続 → 連続 になる普通の写像」
この辺りを理解してないと分からんと思います。
知らなくても雰囲気は分かるかもしれませんが
雰囲気が分かってもあんまり意味がないかも。
開区間 Interval
|| 境界を中に含まない点の集まり
「開集合」の最も代表的な具体例
\begin{array}{llllll} (a,b)&=&\{ x∈R \mid a<x<b \} \end{array}
「開集合」はこれを一般化したものになります。
(開集合に至る発想のスタートはここ)
連続 Continuous
|| 開区間が絶対に持ってる性質
開集合が説明したい感覚
\begin{array}{cccllll} \displaystyle \lim_{x\to c} f(x) &=&f(c) \\ \\ \displaystyle \lim_{|x-c| \to 0} |f(x)-f(c)| &=&0 \end{array}
\begin{array}{llllll} \displaystyle \lim_{x\to c-0} f(x) &=&f(c) &=&\displaystyle \lim_{x\to c+0} f(x) \end{array}
式にするとややこしいですが
要は「繋がってる」っていう感覚の話で
\begin{array}{llllll} \displaystyle |x-c|<δ&&\to&&|f(x)-f(c)|<ε \end{array}
開集合はこれの根っこに来る概念になります。
(実数の性質を表現 ← 集合論)
極限 Limit
|| 近付くっていう感覚の形式表現
「近付ける」っていう操作の数学での名前
\begin{array}{lcclllll} \displaystyle \lim_{x\to c} f(x) &=&f(c) \\ \\ \displaystyle \lim_{n\to \infty} a_n &=&α \end{array}
\begin{array}{ccccrll} \displaystyle |x-c|<δ&&\to&&|f(x)-f(c)|<ε \\ \\ N<n&&\to&&|a_n-α|<ε \end{array}
解析学の基礎中の基礎
そう言って良いほど
これは根っこに近い概念になります。
ユークリッド距離 Euclidean distance
|| 距離の基本的な定義
名前は厳ついですがつまりは距離のこと
\begin{array}{llllll} \displaystyle d(x,y)&=&\displaystyle\sqrt{x^2+y^2} \\ \\ d(x,y,z)&=&\displaystyle\sqrt{x^2+y^2+z^2} \end{array}
開集合の概念は
これが表現することになる
「近さ」を一般化したものになります。
位相 Topology
|| 極限の操作が確実に可能な構造
極限ができない構造を取り除くフィルター τ のこと
\begin{array}{cccccccc} && && && \displaystyle ∅,X&∈&τ \\ \\ ∀O_i &∈&τ &&→&& \displaystyle \bigcup_{i=1}^{\infty}O_i&∈&τ \\ \\ ∀O_i &∈&τ &&→&& \displaystyle \bigcap_{i=1}^{ \textcolor{pink}{n} }O_i&∈&τ \end{array}
距離を使わずに図形を定義する考え方になります。
\begin{array}{llllll} \displaystyle A∩B&⊂&A,B&⊂&A∪B \end{array}
図形的には
常に『中と外がある』
数式的には
\begin{array}{cccccccccccccccccccccl} \displaystyle \textcolor{gray}{∅}&\textcolor{gray}{⊂}& A&⊂& C &⊂&B &\textcolor{gray}{⊂}&\textcolor{gray}{X} \\ \\ && a&<& c &<&b \end{array}
常にこれが成立する
\begin{array}{cccccllllll} \displaystyle 3&<&π&<&4 \\ \\ &&↓&& \\ \\ 3.14&<&π&<&3.15 \end{array}
まあつまり
『確実に大小比較ができる』
ということを「位相」は保証してる感じです。
近傍 Neighborhood
|| 近いという感覚を表現するためのもの
『点』の「視覚的な表現」
あるいは「近似図形」のこと
\begin{array}{llllll} \displaystyle \mathrm{Neighbor}(a,r)&=&\{ x\in R \mid |x-a|<r \} \\ \\ &=&(-r+a,a+r) \end{array}
数式だとあれですが
これは要は『実質的な点』のことで

例えばこれらが交わらないようにとれる時
\begin{array}{llllll} ∃r>0& \displaystyle \mathrm{Neighbor}(a,r)&∩&\displaystyle \mathrm{Neighbor}(b,r)&=&∅ \end{array}
『距離』という概念を使わずに
2 つの点を区別できたり
\begin{array}{ccccccccccll} \mathrm{Point} && \mathrm{closer} && \mathrm{close} \\ \\ \displaystyle \{a\}&⊂& \displaystyle \mathrm{Neighbor}(a,r_1)&⊂&\displaystyle \mathrm{Neighbor}(a,r_2) \end{array}
「近い」という概念を
「部分集合」で定義できたりします。
ちなみに補足しておくと
これもまた「開集合」になります。
( 1 次元なら近傍は開区間です)
開集合 Open Set
|| 位相の具体的な中身
「近傍(見える点)」を厳密に定めるもの
\begin{array}{ccclll} (a-ε,a+ε)&=& \displaystyle\{ x∈R \mid |x-a|<ε \} \\ \\ (a-r,a+r)&=& \displaystyle\{ x∈R \mid \sqrt{x^2+a^2}<r \} \\ \\ (a-ε,a+ε)&⊂&O \end{array}
\begin{array}{llllll} \displaystyle \forall a∈O &\exists ε>0 &(a-ε,a+ε)⊂O \end{array}
数式はこんな感じで
これを満たす「集合 O 」を「開集合」と言います。
ちなみに以下の開区間 B(a,r) には
\begin{array}{cccccc} \displaystyle B(a,r) &=& \displaystyle\{ x∈R \mid |x-a|<r \} \\ \\ &=& (a-r,a+r) \end{array}
\begin{array}{llllll} \displaystyle \forall a∈O &\exists r>0 &B(a,r)⊂O \end{array}
「開球」という名前がついています。
(開球は球形の近傍で r 近傍とも呼ばれます)
定義の解説
ちょっと分かりにくいですが
\begin{array}{llllll} \displaystyle \forall a∈O &\exists ε>0 &(a-ε,a+ε)⊂O \end{array}
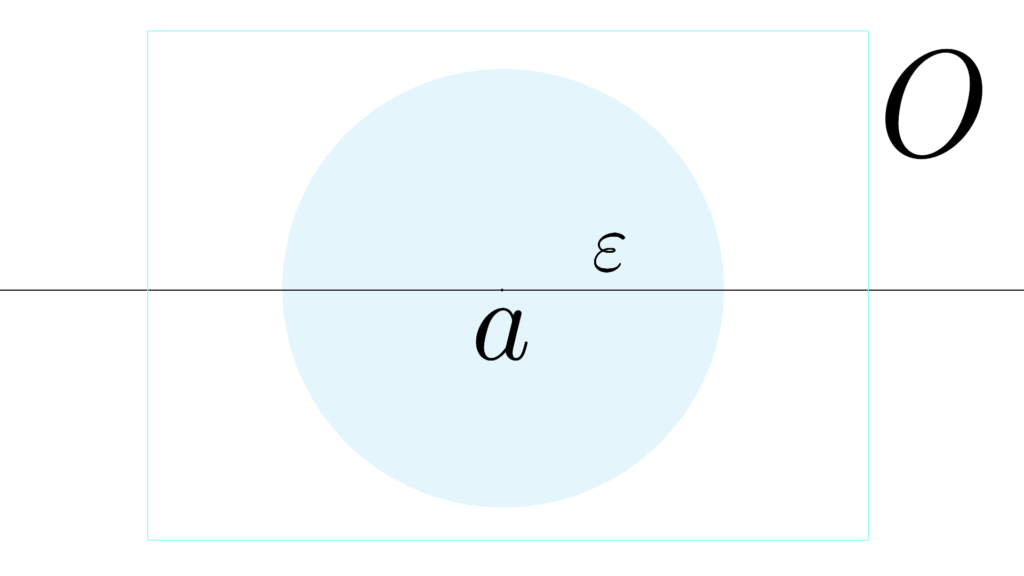
図で見ると
言ってることはわりと単純
O のあらゆる点 a で
「開集合 O の中」に
「集合 (a-ε,a+ε) 」を『必ず作れる』
\begin{array}{ccccccccccll} \displaystyle a&\in& (a-ε,a+ε) \\ \\ a &\in&O \end{array}
『 O には境界の点が含まれてない』から
『 O の端に近い点 a をとっても』
\begin{array}{llllll} \displaystyle (a-ε,a+ε)&⊂&O \end{array}
『連続な集合(区間)が内部に作れる』
つまり『全ての点で開球を作れる』と言ってます。
ちなみに「空集合」についてですが
これにはそもそも『点が存在しない』ので
\begin{array}{llllll} \displaystyle \{\} &⊂&\{\} \end{array}
開集合の定義を満たすと解釈できます。
(条件を満たさない点が無い と言える)
不連続と開集合
不連続な集合(有理数全体)などでは
この「区間 (a-ε,a+ε) 」を内部にとれない
\begin{array}{rrrrrrrrrr} a+0&<&\displaystyle a+\frac{1}{\sqrt{p}}&<& \displaystyle a+\frac{1}{p}&<&a+ε \\ \\ 0&<&\displaystyle \frac{1}{\sqrt{p}}&<& \displaystyle \frac{1}{p}&<&ε \end{array}
より具体的には
(a-ε,a+ε) は必ず中に無理数を含むので
\begin{array}{llllll} \displaystyle p&\in&\mathrm{Prime \,\, Number} \end{array}
\begin{array}{llllll} \displaystyle a+\frac{1}{\sqrt{p}} &\not\in&Q \end{array}
「自然数全体」「有理数全体」
こういった不連続な集合は
「開集合ではない」ということになります。
境界を含む場合と開集合
境界を内部に含む集合(半開区間など)も
この開集合の定義を満たしません。
\begin{array}{llllll} \displaystyle [α,β) \end{array}
というのも
「境界の点 α 」を考えると
\begin{array}{llllll} \displaystyle α-ε&\not\in&[α,β) \end{array}
この境界の点 α では
\begin{array}{llllll} \displaystyle α&\in&[α,β) \end{array}
α は [α,β) に含まれる点なのに
(α-ε,α+ε) が [α,β) から必ず溢れてしまう
\begin{array}{llllll} \displaystyle (α-ε,α+ε)&\not\subset&O \\ \\ \\ (a-ε,a+ε)&\subset&O &&× \end{array}
つまり任意の [α,β) の点 a でこうならないので
半開区間は開集合ではないということになります。
開区間が開集合であることの確認
開区間は開集合の雛型です。
なのでもちろん開区間は開集合なんですが
\begin{array}{llllll} \displaystyle (a-ε,a+ε) &⊂&(α,β) \end{array}
定義に問題があるかもしれないので
念のため確認しておきます。
というわけで
とりあえず区間を「点 x 」で適当に2分割し
\begin{array}{llllll} \displaystyle ε&=&\min\Bigl( \{ |x-α|,|β-x| \} \Bigr) \end{array}
ε をこのようにとってみます。
\begin{array}{llllll} \displaystyle (x-ε,x+ε)&⊂& (α,β) \end{array}
すると、確実に内側に含む開球が作れる
つまり「開集合」の定義が満たされるので
「任意の開区間 (α,β) は開集合である」と言えます。
無限区間も開集合
(0,\infty) のような形の
無限区間もまた開集合になります。
\begin{array}{llllll} \displaystyle a&∈&(0,\infty) \end{array}
具体的には
(0,\infty) の中にある任意の点 a を考えて
\begin{array}{llllll} \displaystyle ε&≤&a \end{array}
ε をこの範囲でとると
\begin{array}{llllll} \displaystyle B(a,ε)&=&(a-ε,a+ε) \\ \\ B(a,a)&=&(a-a,a+a) &=&(0,2a) \end{array}
必ず開球を (0,\infty) の中に作れることから
\begin{array}{llllll} \displaystyle (0,2a)&\subset&(0,\infty) \end{array}
結果、開集合の定義を満たすので
(0,\infty) もまた開集合であると言えます。
定義の導出過程
当然の話ですが
\begin{array}{llllll} \displaystyle \forall a∈O &\exists ε>0 &(a-ε,a+ε)⊂O \end{array}
これは『後から』定められたもので
最初から分かっていたわけではありません。
定義は成果で
\begin{array}{cccll} \displaystyle (α,β)&\in&\mathrm{Open \,\, Set} \\ \\ (α,\infty)&\in&\mathrm{Open \,\, Set} \\ \\ \\ [α,β)&\not\in&\mathrm{Open \,\, Set} \\ \\ N&\not\in&\mathrm{Open \,\, Set} \end{array}
順番はこっちが先です。
(これを満たす条件が開集合の定義)
「開球」については
\begin{array}{cccccc} \displaystyle B(a,r) &=& \displaystyle\{ x∈R \mid |x-a|<r \} \\ \\ &=& (a-r,a+r) \end{array}
『開集合の構成要素』を考えると
「近傍」の考え方などから
自然とその存在が導かれ
そこから開集合を構成していくと
\begin{array}{lllllcll} & \exists ε>0 &(a-ε,a+ε)⊂O &&& 1 & \mathrm{Point}\\ \\ \displaystyle \forall a∈O & \exists ε>0 &(a-ε,a+ε)⊂O &&& \mathrm{All} & \mathrm{Point}\end{array}
これらの条件は
\begin{array}{ccccccccll} \displaystyle (α,β)&\in&\mathrm{Open \,\, Set} && \mathrm{All} \\ \\ (α,\infty)&\in&\mathrm{Open \,\, Set} && \mathrm{All} \\ \\ \\ [α,β)&\not\in&\mathrm{Open \,\, Set} && α \\ \\ N&\not\in&\mathrm{Open \,\, Set} && \mathrm{No} \end{array}
この要望から導かれます。
位相と開集合
「開集合の共通部分」が有限個で定義されている
\begin{array}{llllll} \displaystyle ∀O_i &∈&τ &&→&& \displaystyle \bigcap_{i=1}^{ \textcolor{pink}{n} }O_i&∈&τ \end{array}
この「位相」の定義の由来は
\begin{array}{llllll} \displaystyle ∀O_i &∈&τ &&→&& \displaystyle \bigcap_{i=1}^{ \textcolor{pink}{\infty} }O_i&∈&τ &&×\end{array}
もちろんこうならないからなんですが
\begin{array}{llllll} \displaystyle \bigcap_{i=1}^{ \textcolor{pink}{\infty} }O_i&\not\in&τ \end{array}
なんでこうなるのか
この時点ではよく分からないと思うので
きちんと確認しておきます。
と言っても話は単純
\begin{array}{llllll} \displaystyle \left(a-\frac{1}{n} , b+\frac{1}{n} \right)&\in&τ \end{array}
こういう開集合を考えると
\begin{array}{llllll} \displaystyle \bigcap_{n=1}^{\infty}A_n&=&[a,b] \end{array}
こうなるので
これが開集合にならないことはすぐに分かります。
閉集合 Closed Set
|| 開集合への補集合操作による結果
補集合をとると開集合になる集合
\begin{array}{llllll} \displaystyle \forall a∈O &\exists ε>0 &(a-ε,a+ε)⊂O \end{array}
\begin{array}{llllll} \displaystyle O^c&∈&\mathrm{Closed \,\, Set} \end{array}
定義はこんな感じで
\begin{array}{llllll} \displaystyle \{a\}&∈&\mathrm{Closed \,\, Set} \end{array}
具体的にはこういうのが閉集合になります。
点は閉集合
「点」は内部に「開球」を作れませんから
「点集合 \{a\} 」は「開集合」ではありません。
\begin{array}{cclllll} \{a\} \\ \\ \displaystyle \overline{ \{a\} } &=& R\setminus \{a\} \end{array}
ただ、その「補集合」はこうで
これは「開集合」になりそうです。
というわけで確認してみると
\begin{array}{llllll} \displaystyle B(c,ε) &=& \displaystyle\{ x∈R \mid |x-c|<ε \} \\ \\ &=& (c-ε,c+ε) \end{array}
開球はこうですから
\begin{array}{llllll} \displaystyle (c-ε,c+ε)&⊂&(a,\infty) \\ \\ (c-ε,c+ε)&⊂&(-\infty,a) \end{array}
点 a の近くを考えて
中に納まるよう ε を調整すると
\begin{array}{llllll} \displaystyle && a&<&c-ε \\ \\ c+ε&<& a \end{array}
必ずこのどちらかになるので
\begin{array}{llllll} \displaystyle ε&<&c-a \\ \\ ε&<&a-c \end{array}
結果として
\begin{array}{llllll} ε&<&\displaystyle |c-a| \end{array}
こんな条件が導けるため
\begin{array}{llllll} \displaystyle ε&=&\displaystyle\frac{1}{2}|c-a| \end{array}
例えばこのように ε をとれば
全ての点で開集合をとることができます。
開集合と閉集合は両立する
「開集合」の『補集合』という点で
なんとなく分かると思いますが
\begin{array}{cccll} R&=&\overline{∅} \\ \\ \displaystyle \overline{R}&=&∅ \end{array}
例えばこのような場合
「開集合の補集合」→「閉集合」となるので
\begin{array}{ccllllll} R&\in&\mathrm{Open \,\, Set} \\ \\ \displaystyle \overline{R}&\in&\mathrm{Closed \,\, Set} \\ \\ ∅&\in&\mathrm{Open \,\, Set} \\ \\ \overline{∅}&\in&\mathrm{Closed \,\, Set} \end{array}
実はこの「閉集合」という概念は
「開集合」と排反ではありません。
「開かつ閉」という状態はあり得ます。
開集合でも閉集合でもない集合がある
「有理数全体 Q 」は開集合ではない
となると「じゃあ閉集合?」となりますが
\begin{array}{rllllll} \displaystyle Q&\not\in&\mathrm{Open \,\, Set} \\ \\ R\setminus Q &\not\in&\mathrm{Open \,\, Set} \\ \\ \displaystyle Q&\not\in&\mathrm{Closed \,\, Set} \end{array}
実は「有理数全体」は
『開集合でも閉集合でもない』ものになります。
というのも
これは「有理数」が持ってる
『稠密性』という性質が悪さしてる感じで
\begin{array}{ccccrcccc} \displaystyle a&<&q&<&a+ε \\ \\ 0&<&x-a&<&ε \end{array}
例えば「有理数の補集合」をとった上で
以下のような「無理数」を考えた場合
\begin{array}{llllll} \displaystyle π&\in&R\setminus Q \end{array}
「任意の区間」の内部には
\begin{array}{llllll} \displaystyle π&<& q &<&π+ε \end{array}
\begin{array}{rrrrrll} 0 &<& \displaystyle q_ε&<&ε \end{array}
\begin{array}{llllll} \displaystyle 3.141592&<&π&<&3.141593 \end{array}
「必ず有理数と無理数が存在する」ことから
\begin{array}{llllll} \displaystyle (π-ε,π+ε)&\not\subset&R\setminus Q \end{array}
「有理数の補集合 R\setminus Q 」の内部には
この点 π で間違いなく「開球」が『作れません』
となると
『任意の点』では内部に含む開球を作れない
つまり「開集合の定義」を満たさないので
「有理数の補集合 \overline{Q} 」は「開集合ではない」
\begin{array}{llllll} \overline{Q}&=& \displaystyle R\setminus Q \end{array}
つまり
「有理数全体」は
「閉集合でもない」ということになります。
半開区間は閉集合?
↑ で示したように
「半開区間」は「開集合」ではありません。
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle α-ε&\not\in&[α,β) \end{array} \end{array}
となると
じゃあ「閉集合」か? ってなりますが
\begin{array}{llllll} \displaystyle [α,β)^c&=&(-\infty,α)∪[β,\infty) \end{array}
「閉集合である」と『仮定』しつつ
「補集合」をとって「開集合にしてみる」と
\begin{array}{ccccr} ε=β-α &&→&& \displaystyle β-ε<β \\ \\ \displaystyle ε=\frac{β-α}{2} &&→&& \displaystyle α<β-ε<β \end{array}
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle β-ε&\not\in&(-\infty,α)∪[β,\infty) \end{array} \end{array}
明らかに β-ε では「開球」を作れない
つまり「開集合」の条件を満たさないので
\begin{array}{llllll} \displaystyle [α,β) \\ \\ (α,β] \end{array}
実はこれらもまた
「開集合」でも「閉集合」でもない集合になります。
閉集合の役割
整理しておくと
「開集合」というのは
\begin{array}{llllll} &\exists ε>0 &(a-ε,a+ε)⊂O \\ \\ \displaystyle \forall a∈O &\exists ε>0 &(a-ε,a+ε)⊂O \end{array}
『全ての点』で『開球を作れる』
『全ての点』で『連続』を定義できる
そんな集合で
\begin{array}{rrrrrrrlll} \displaystyle O_1,O_2,...∈\mathrm{Open \,\, Set} &&→&&\displaystyle \bigcup_{n=1}^{\infty}O_n∈\mathrm{Open \,\, Set} \\ \\ \displaystyle O_1,O_2,...∈\mathrm{Open \,\, Set} &&→&&\displaystyle \bigcap_{i=1}^{n}O_i∈\mathrm{Open \,\, Set} \end{array}
「和集合」操作と
「有限回の共通部分」操作については閉じてますが
(閉じてるってのは 開集合 → 開集合 になる感じ)
「補集合」操作を行う場合
\begin{array}{ccccccclllll} \displaystyle (-\infty,a)∪(a,\infty)&&→&&\{a\} \\ \\ \displaystyle (-\infty,a)∪(b,\infty)&&→&&[a,b] \end{array}
「点」や「境界を含む区間」が得られて
『不連続』という状態になり得てしまうので
閉じているとは言えません。
ここで定義されたのが
「閉集合」という概念で
\begin{array}{llllll} \displaystyle \Bigl( \mathrm{Open \,\, Set} \Bigr)^c&=&\mathrm{Closed \,\, Set} \end{array}
こいつは「境界を含む」「不連続」
そういった性質を許容しています。
\begin{array}{cccccccllllll} \displaystyle \mathrm{Point} &∈&\mathrm{Closed \,\, Set} \\ \\ \displaystyle \mathrm{Closed \,\, Interval} &∈&\mathrm{Closed \,\, Set} \end{array}
まあつまり
「点」「不連続」「境界を含む」
こういった概念を説明するのに必要不可欠で
\begin{array}{llllll} \displaystyle \{a\}&∈&\mathrm{Closed \,\, Set} \\ \\ [a,b]&∈&\mathrm{Closed \,\, Set} \end{array}
閉集合はそのために存在しています。
まとめると
確実に「連続」という操作が保証されている
これを可能な限りカバーしてるのが「開集合」
必ずしも「連続」が保証されていない
それらをだいたいカバーしてるのが「閉集合」です。
(他のやつはボレル集合で補完される)
連続写像 Continuous Function
|| よく使う普通でシンプルな関数のこと
「連続」→「連続」になる関数のこと
\begin{array}{llllll} B_r(a)&=&\{ x∈R \mid -r+a<x<a+r \} \\ \\ &=&\{ x∈R \mid |x-a|<r \} \\ \\ &=&(-r+a,a+r) \end{array}
\begin{array}{llllll} \displaystyle \mathrm{Open \,\,Set} &&→&&\mathrm{Open \,\,Set} \end{array}
\begin{array}{cccccccccccc} \displaystyle ∀ε &∃δ && f\Bigl( B_δ(a) \Bigr) &⊂& B_ε \Bigl(f(a) \Bigr) \\ \\ ∀ε &∃δ && B_δ(a) &⊂& f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr)\end{array}
「開集合」を使った厳密な定義は
こういうよく分からん感じになっています。
(省略してますが正確には ε,δ>0 です)
定義の解説
「像 f(a) で作れる任意の開球」
つまりは「ほぼ点 f(a) の開球」なんかを考えた時
\begin{array}{ccccc} f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) &&←&& \displaystyle B_ε \Bigl(f(a) \Bigr) \\ \\ f^{-1} \Bigl( (-ε +f(a),f(a)+ε) \Bigr) &&←&& ( -ε +f(a),f(a)+ε ) \end{array}
その「逆像 f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) 」の中に
\begin{array}{cccccccc} a&=&f^{-1} \Bigl(f(a) \Bigr) \\ \\ \displaystyle B_δ(a) &⊂& f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) \end{array}
必ず「開球 B_δ(a) が作れる」
まとめると
「開球 B_ε \Bigl(f(a) \Bigr) (開集合)」を変数にすると
\begin{array}{llllll} \displaystyle B_δ(a) &⊂& f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) \end{array}
「どれだけ小さな ε であっても」
「どれだけ開球 B_ε \Bigl(f(a) \Bigr) が小さくても」
必ず「点 a を中心とした」
「開球 B_δ(a) が作れる」
つまり
「像が開集合」なら
「定義域も開集合である」
\begin{array}{llllll} \displaystyle \mathrm{Open \,\,Set} &&←&&\mathrm{Open \,\,Set} \end{array}
と言ってるだけなので
そんな難しく考えなくて良いです。
連続のままとは
これについては
\begin{array}{llllll} \displaystyle \lim_{x\to a}x&=&a &&&⇒&&& \displaystyle \lim_{x\to a}f(x)&=&f(a) \end{array}
「連続」の定義から
\begin{array}{cccccccccc} \displaystyle x&∈&A &&→&& f(x)&∈&B \\ \\ \\ && &&&& f(A)&⊂&B \\ \\ f^{-1}(B)&⊂&A &&&& && \end{array}
\begin{array}{llllll} \displaystyle A & \mathrm{Continuous} &&→&&B_δ(a) \\ \\ B & \mathrm{Continuous} &&→&&B_ε\Bigl( f(a) \Bigr) \end{array}
記号で見た方が
話としてはシンプルかもしれません。
開集合 → 開集合
「連続写像」の定義は
\begin{array}{llllll} \displaystyle \mathrm{Open \,\,Set} &&→&&\mathrm{Open \,\,Set} \end{array}
これが先に来ます。
\begin{array}{llllll} \displaystyle ∀ε &∃δ && B_δ(a) &⊂& f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) \end{array}
これはその表現の一つで
\begin{array}{llllll} \displaystyle ∀V∈\mathrm{Neighbor}\Bigl(f(a) \Bigr)&f^{-1}(V)∈\mathrm{Neighbor}(a) \end{array}
例えば『連続を保証する最小単位』として
「開集合」の替わりに「近傍」を使うと
このように書けたりします。
意味は
V∈\mathrm{Neighbor}\Bigl(f(a) \Bigr)
「像 f(a) の近傍 V 」を考えた時
\begin{array}{llllll} \displaystyle f^{-1}(V)∈\mathrm{Neighbor}(a) \end{array}
その「逆像 f^{-1}(V) 」は
「全て」「 a の近傍」になる
\begin{array}{ccccccccccccc} \displaystyle f^{-1}&:& f^{-1}(V) &←&V \\ \\ && \mathrm{Open \,\,Set} &←&\mathrm{Open \,\,Set} \end{array}
という感じ。
連続写像と閉集合
定義から分かる通り
\begin{array}{llllll} \displaystyle \mathrm{Open \,\,Set} &&→&&\mathrm{Open \,\,Set} \end{array}
連続写像は「開集合 → 開集合」になる写像です。
しかし具体的に
例えば「恒等写像 \mathrm{Id} 」を考えてみると
\begin{array}{llllll} \displaystyle \mathrm{Id}&:&O&\to&O \end{array}
\begin{array}{ccccccclll} \displaystyle \mathrm{Id}^{-1}(O) &\mathrm{Id}(O) \\ \\ O & O \end{array}
これは間違いなく「連続写像」ですが
\begin{array}{cccccc} \displaystyle x&:&\{a\}&\to&\{a\} \\ \\ x&:&[a,b)&\to&[a,b) \end{array}
これの変数に「閉集合の要素」を入れても
特に問題らしい問題は発生しません。
なにより
「連続写像」の定義を見ても
\begin{array}{llllll} \displaystyle ∀ε &∃δ && B_δ(a) &⊂& f^{-1}\Bigl( B_ε \Bigl(f(a) \Bigr) \Bigr) \end{array}
これは「開集合が定義域の場合の話」であって
それ以上のことは言及されていません。
まあつまり何が言いたいかというと
「連続写像である」ことと
「写像の定義域」は別の話になります。
閉集合による連続写像の特徴付け
↑ の話を代表する分かりやすい例として
「閉集合」による定義を紹介しておきます。
\begin{array}{rrrrrrrrrr} \displaystyle \mathrm{Open \,\,Set} &&→&&\mathrm{Open \,\,Set} \\ \\ \mathrm{Closed \,\,Set} &&→&&\mathrm{Closed \,\,Set} \end{array}
結論はこう
\begin{array}{llllll} \displaystyle f&:&X&→&Y \end{array}
f を「連続関数である」とすると
\begin{array}{ccccccc} \displaystyle f^{-1}(C_Y)&⊂&X \\ \\ C_Y&⊂&Y \end{array}
「閉集合」の定義が
「開集合の補集合である」こと
\begin{array}{ccccccccccc} \displaystyle \Bigl( C_Y \Bigr)^c&=&Y\setminus C_Y&∈&\mathrm{Open \,\, Set} \\ \\ && f^{-1}(Y\setminus C_Y)&∈&\mathrm{Open \,\, Set} \end{array}
そして「連続関数である」という前提から
\begin{array}{ccccccccccccc} f(X)\setminus f(A) &⊂&f(X\setminus A) \\ \\ f^{-1}(Y)\setminus f^{-1}(B) &=& \displaystyle f^{-1}(Y\setminus B) \end{array}
\begin{array}{ccrcccccc} f^{-1}(Y\setminus C_Y ) &=&f^{-1}(Y)\setminus f^{-1}(C_Y)&∈&\mathrm{Open \,\, Set} \\ \\ &=& \displaystyle X\setminus f^{-1}(C_Y) &∈&\mathrm{Open \,\, Set} \\ \\ &=& \displaystyle \Bigl( f^{-1}(C_Y) \Bigr)^c &∈&\mathrm{Open \,\, Set} \end{array}
こうなり
これで「 f は連続関数である」から
「閉集合→閉集合」という
「閉集合による条件」が導けて
後はこの逆を辿れば
\begin{array}{cccccccccccc} C_Y &∈&\mathrm{Closed \,\, Set}&&→&& \displaystyle \Bigl( C_Y \Bigr)^c &∈&\mathrm{Open \,\, Set} \\ \\ &↓& && && &↓& \\ \\ f^{-1}(C_Y) &∈&\mathrm{Closed \,\, Set}&&→&& \displaystyle \Bigl( f^{-1}(C_Y) \Bigr)^c &∈&\mathrm{Open \,\, Set} \end{array}
「閉集合による条件(定義)」から
\begin{array}{llllll} \displaystyle \mathrm{Open \,\,Set} &&→&&\mathrm{Open \,\,Set} \end{array}
そのまま「連続である」という結論を導けるため
結果として
「開集合→開集合」になる
「閉集合→閉集合」になる
\begin{array}{llllll} \displaystyle & f \,\, \mathrm{is \,\, Continuous} \\ \\ ⇔&O_Y,f^{-1}(O_Y)∈\mathrm{Open \,\, Set} \\ \\ ⇔&C_Y,f^{-1}(C_Y)∈\mathrm{Closed \,\, Set} \end{array}
これらが「連続関数である」と同値である
ということが分かります。
