|| 2変数以上の関数を微分する時使うやつ
1変数だけ動かす微分のこと
スポンサーリンク
これらの記事を見ておくことを推奨します。
\begin{array}{lllllll} \displaystyle \frac{\partial f(x,y)}{\partial x}&=&\displaystyle \lim_{h→0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \\ \\ \displaystyle \frac{\partial f(x,y)}{\partial y}&=&\displaystyle \lim_{h→0}\frac{f(x,y+h)-f(x,y)}{(y+h)-y} \end{array}
見なくてもなんとなく分かるよう
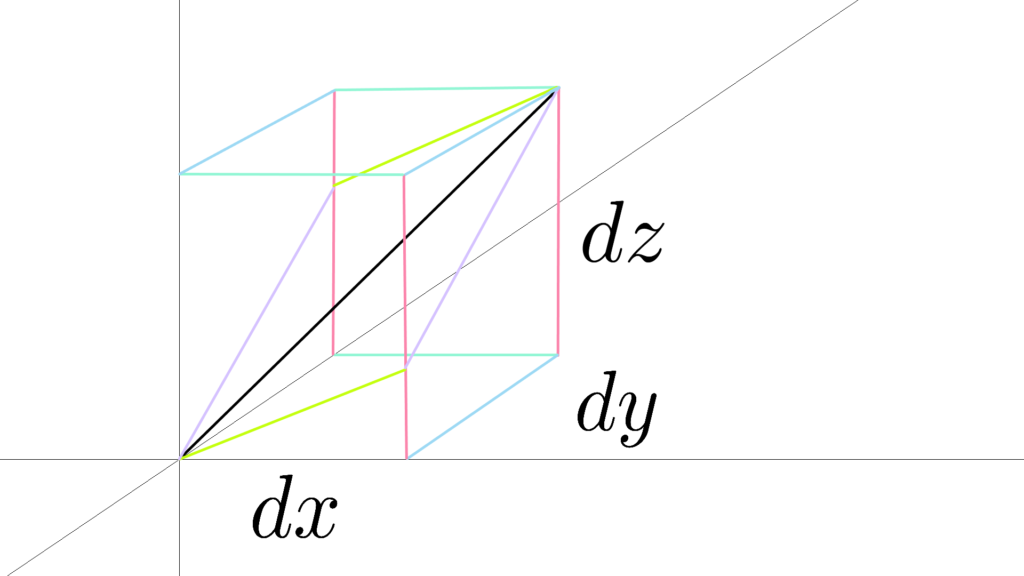
\begin{array}{llllll} z&=&f(x,y) \\ \\ z+dz &=& \displaystyle f(x+dx,y+dy) \\ \\ z+dz &=&f(x,y)+df(x+dx,y)+df(x,y+dy) \end{array}
感覚的な話も交えてはいますが
「微分」が分からないまま「偏微分」を知る
この流れは推奨しません。
目次
全微分「全ての変数を同時に動かす」
偏微分「他を固定して1つの変数だけ動かす」
全微分 Total Differential
|| 好きに変数を動かす微分のやり方
多変数関数で定義される微分の名前
\begin{array}{llll} \displaystyle dz&=&df(x,y) \\ \\ &=&f(x+dx,y+dy)-f(x,y) \end{array}
記号だとこんな感じ。

\begin{array}{rlll} \displaystyle df&\displaystyle =&\displaystyle\frac{\partial f}{\partial x}dx&\displaystyle +\frac{\partial f}{\partial y}dy \\ \\ \displaystyle \frac{d}{dt}f&\displaystyle =&\displaystyle\frac{\partial f}{\partial x}\frac{dx}{dt}&\displaystyle +\frac{\partial f}{\partial y}\frac{dy}{dt} \end{array}
見た目は複雑ですけど
↑ のは座標を表してるだけです。
難しいことはなにも言ってません。
偏微分 Partial Differentiation
|| 1つの変数だけ動かす微分
『関数と1つの変数だけ』に注目し
『他の点を固定(定数に)』してからやる微分
\begin{array}{lllllll} \displaystyle \frac{\partial f(x,y)}{\partial x}&=&\displaystyle \lim_{h→0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \\ \\ \displaystyle \frac{\partial f(x,y)}{\partial y}&=&\displaystyle \lim_{h→0}\frac{f(x,y+h)-f(x,y)}{(y+h)-y} \end{array}
2変数関数 z=f(x,y) なんかの微分を考える時
「全ての変数を動かす」操作はよく分からないので
\begin{array}{llllll} \displaystyle x,y&&→&&x,c \\ \\ x,y&&→&&c,y \end{array}
「多変数関数の微分」を考える時
この「偏微分」という操作は絶対必要になります。
\begin{array}{ccccccccc} \displaystyle \frac{\partial}{\partial x}f(x,y)&&\displaystyle\frac{\partial}{\partial x}f&&\displaystyle\frac{\partial f}{\partial x} \\ \\ \displaystyle \frac{\partial}{\partial y}f(x,y)&&\displaystyle\frac{\partial}{\partial y}f&&\displaystyle\frac{\partial f}{\partial y} \end{array}
ちなみに普通の微分と同様
「偏微分」が求めるのは『接線の傾き』です。
( x,z 平面と y,z 平面でそれぞれ求めている)
具体的な感じ
「偏微分」がやってることは
「1変数の微分」とほぼ同じです。
f(x,y)=x^2+y^2
\begin{array}{llllllllll} \displaystyle \frac{\partial}{\partial x}f(x,y)&=&(x^2)^{\prime}+(y^2)^{\prime} \\ \\ &=&2x \\ \\ \\ \displaystyle \frac{\partial}{\partial y}f(x,y)&=&(x^2)^{\prime}+(y^2)^{\prime} \\ \\ &=&2y \end{array}
「微分」が分かっているなら
すぐに分かると思います。
全微分と偏微分
確認しておくと
「多変数関数の微分」というのは
\begin{array}{llllll} \displaystyle dz&=&f(x+dx,y+dy)-f(x,y) \end{array}

「全微分」を指します。
\begin{array}{rlll} \displaystyle df&\displaystyle =&\displaystyle\frac{\partial f}{\partial x}dx&\displaystyle +\frac{\partial f}{\partial y}dy \\ \\ \displaystyle \frac{d}{dt}f&\displaystyle =&\displaystyle\frac{\partial f}{\partial x}\frac{dx}{dt}&\displaystyle +\frac{\partial f}{\partial y}\frac{dy}{dt} \end{array}
「変数を1つずつ動かす」わけではありません。
これは『全ての変数を同時に動かす』操作です。
\begin{array}{cllllll} \displaystyle \frac{df(x)}{dx} \\ \\ \displaystyle\frac{\partial f(x,y)}{\partial x} \end{array}
「偏微分」や「1変数の全微分」とは
根本的に異なる操作になります。
全微分とは
結論を先取りせず考えると
\begin{array}{llllll} \displaystyle f^{\prime}(x,y) \end{array}
「全微分」はよく分かりません。
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0}\frac{f(x+h)-f(x)}{(x+h)-x} \end{array}
「1変数の微分」は分かりますが
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0}\frac{f(x+h,y+h)-f(x,y)}{(x+h,y+h)-(x,y)} \end{array}
「多変数」となるとさっぱりです。
どのように計算すれば良いのか
そもそも計算はできるのか
そういった基本的なことさえ
なにも分かりません。
分かる操作
「1変数の微分」は分かる
これは確かなので
\begin{array}{llllll} \displaystyle \displaystyle\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \end{array}
「多変数関数の微分」を考える上で
このような操作は自然な発想から導かれます。
\begin{array}{llllll} \displaystyle \frac{\partial f(x,y)}{\partial x}&=&\displaystyle\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \end{array}
これがどのような役割を持つのか
「全微分」とどう関わっているのか
この時点では
そういったことは一切分かりませんが
この操作の存在自体は事実ですし
これがこれから必要になるだろうことは
直感的になんとなく予想できます。
座標
「全微分」の操作を調べるために
『実際に図示してみる』
\begin{array}{llll} \displaystyle dz&=df(x,y) \\ \\ &=f(x+dx,y+dy)-f(x,y) \end{array}
そんな単純な発想から
「全微分」の具体的な中身ははっきりします。
\begin{array}{llc} x,y+dy&x+dx,y+dy \\ \\ x,y&x+dx,y \end{array}

\begin{array}{llc} 0,dy&dx,dy \\ \\ 0,0&dx,0 \end{array}
\begin{array}{rllll} \displaystyle f(x,y)&=&x+y \\ \\ \\ f(0,0)&=&0+0 \\ \\ \\ &&f(0+1,0)&=&1+0 \\ \\ &&f(0,0+1)&=&0+1 \\ \\ \\ &&&&f(0+1,0+1)&=&1+1 \end{array}
「 x,y を動かした時」の
「 z の動き」はこのようになるので
\begin{array}{llllll} f(x+dx,y)&=&f(x,y)+df(x+dx,y) \\ \\ f(x,y+dy)&=&f(x,y)+df(x,y+dy) \\ \\ \\ \\ z+dz&=&f(x,y)+df(x+dx,y+dy) \\ \\ &=&f(x+dx,y+dy) \\ \\ \\ &=& \displaystyle f(x,y)+df(x+dx,y)+df(x,y+dy) \end{array}

「 z の微小変化 dz 」に関しては
このように「座標」の足し算で表現可能
\begin{array}{rlllll} dz&=&\displaystyle df(x+dx,y+dy) \\ \\ &=&df(x+dx,y)+df(x,y+dy) \end{array}
一般形はちょっとややこしいですが
\begin{array}{llllll} \displaystyle f(0,0)&=&0 \end{array}
\begin{array}{llllll} f(0+dx,0)&=&f(0,0)+df(0+dx,0) \\ \\ &=&df(dx,0) \\ \\ \\ f(0,0+dy)&=&f(0,0)+df(0,0+dy) \\ \\ &=&df(0,dy) \\ \\ \\ \\ z+dz&=&f(0,0)+df(0+dx,0+dy) \\ \\ &=&f(0+dx,0+dy) \\ \\ &=&f(dx,dy) \\ \\ \\ &=& \displaystyle f(0,0)+df(0+dx,0)+df(0,0+dy) \\ \\ &=&df(dx,0)+df(0,dy) \end{array}
このように考えると
ただの足し算で全微分が導けます。
偏微分での表現
座標の足し算で ↓ が分かりました。
\begin{array}{rlllll} dz&=&df(x+dx,y)+df(x,y+dy) \end{array}
といっても
これはこのままではよく分からないので
分かる形にしなければなりません。
\begin{array}{llllll} \displaystyle df(x+dx,y) \\ \\ df(x,y+dy) \end{array}
そのためには
よく分からないこの部分をどうにかする必要が。
とまあそういうわけなので
この部分について見ていくと
\begin{array}{llllll} \displaystyle df(x+dx,y) \end{array}
「 x を dx だけ動かした f 」という
これの意味自体はすぐに分かって
これは y を動かさない操作なので
『 x の変化による z=f(x,y) の変化』を
x,z 平面だけで考えることができる
\begin{array}{llllll} \displaystyle a \\ \\ ax&=&y \end{array}
\begin{array}{llllll} \displaystyle \frac{\partial f(x,y)}{\partial x} \\ \\ \displaystyle \frac{\partial f(x,y)}{\partial x}dx&=&df(x,y) \end{array}
その上で「傾き」を使い
座標を書き直してみると
\begin{array}{llrlc} \displaystyle f(x+dx,y)&=&\displaystyle f(x,y)+\frac{\partial f(x,y)}{\partial x}dx \\ \\ \displaystyle f(x+dx,y)-f(x,y) &=&\displaystyle \frac{\partial z}{\partial x}dx \end{array}
これはこのように表現できて
同じように
y,z 平面で考えてみると
\begin{array}{llllll} \displaystyle \displaystyle f(x,y+dy)-f(x,y) &=&\displaystyle\frac{\partial z}{\partial y}dy \end{array}
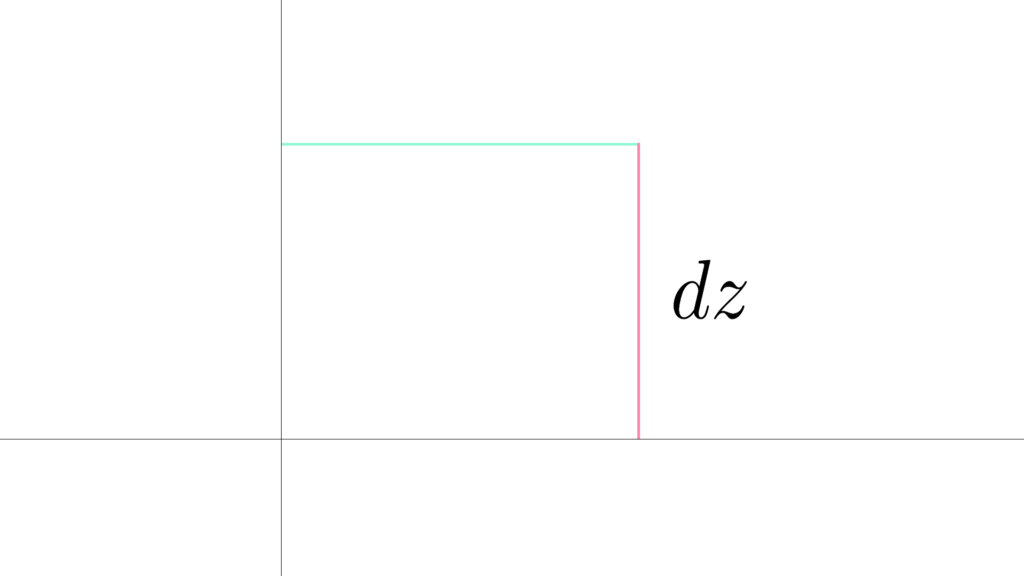
こっちもこんな感じになります。
多変数関数の微小変化
以上のことが分かったので
\begin{array}{llllll} \displaystyle \displaystyle \partial x&=&\displaystyle \lim_{h→0}(x+h)-x \\ \\ dx&=&\displaystyle \lim_{h→0}(x+h)-x \end{array}

\begin{array}{llr} \displaystyle \frac{\partial z}{\partial x} &=&\displaystyle \lim_{h→0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \\ \\ &=&\displaystyle \frac{f(x+dx,y)-f(x,y)}{dx} \end{array}
x,y の両方を動かした時の
多変数関数 z の微小変化 dz は
\begin{array}{llllllll} \displaystyle f(x+dx,y)-f(x,y) &=&\displaystyle df(x+dx,y) \\ \\ &=&\displaystyle \frac{\partial f(x,y)}{\partial x}dx \\ \\ \\ \displaystyle f(x,y+dy)-f(x,y)&=&\displaystyle df(x,y+dy) \\ \\&=&\displaystyle \frac{\partial f(x,y)}{\partial y}dy \end{array}
座標の計算から ↓ のようになる
\begin{array}{lllllll}z+dz&=&\displaystyle f(x+dx,y+dy) \\ \\ &=&f(x,y)+df(x+dx,y)+df(x,y+dy) \\ \\ \\ &=&\displaystyle f(x,y)+\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy \end{array}
\begin{array}{llllll}\displaystyle dz&=&f(x+dx,y+dy)-f(x,y) \\ \\ &=&\displaystyle \frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy \end{array}
座標 z+dz を求める手順から
これはすぐに分かると思います。
\begin{array}{lllllll} dz&=&\displaystyle df(x+dx,y+dy) \\ \\ &=&\displaystyle \frac{\partial }{\partial x}f(x,y)\,dx+\frac{\partial }{\partial y}f(x,y) \,dy \end{array}
以上
これで「微小変化 dz 」の詳細が判明しました。
全微分と偏微分
全ての変数を一気に動かしたいなら
\begin{array}{rlll} \displaystyle x&=&x(t)&&\Bigl( \cos t,r \cos t ,\cdots \Bigr) \\ \\ \displaystyle y&=&y(t)&&\Bigl( \sin t,r\sin t ,\cdots \Bigr) \end{array}
x,y の両方が t で変化するような
そんな変数 t を定義する必要があります。
ここで使えるのが「極座標」で
\begin{array}{llllll} \displaystyle x&=&r \cos t \\ \\ y&=&r\sin t \end{array}
例えばこうすれば
全微分は ↓ みたいに書くことができて
\begin{array}{llllll} \displaystyle z&=&f(x,y) \\ \\ &=&φ\Bigl( x(t),y(t) \Bigr) \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \frac{dz}{dt}&=&\displaystyle\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} \end{array}
結果
「多変数関数の微分」が求められます。
変数はだいたいなんでもいい
最後、補足しておくと
\begin{array}{llllll} \displaystyle x&=&r\cos θ \\ y&=&r\sin θ \end{array}
↑ で話した「全微分」の結果は
「極座標系」であっても
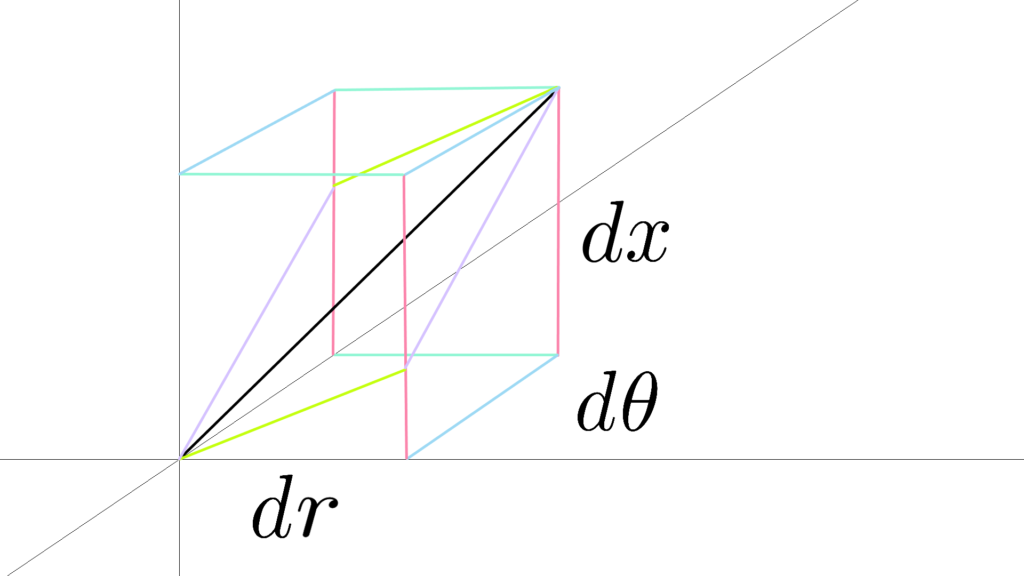
結局のところ
「微小変化」はこのような形になるので
x,y も r,θ も同様の結果になります。
