|| ジョルダン測度などを抽象化したやつ
「測度空間」から「可測空間」を抜いた感じ
スポンサーリンク
事前知識
完全加法族「矛盾なく足し算ができる枠組み」
有限加法族「完全加法族より条件が緩いやつ」
区間(最低限)「基本集合を定義するやつ」
測度「面積とかの性質を満たす集合関数」
可測空間「実数全体とかを完全加法族に加工したやつ」
測度空間「可測空間に測度を付け足したやつ」
目次
前測度「測度っぽいものにつく名前」
ジョルダン測度「長さとかを求める直感的な操作」
前測度 Pre-Measure
|| めちゃくちゃ抽象化された測度の名前
「測度っぽいもの μ 」のことで
\begin{array}{ccccc} ? &&&& 〇 \\ \\ \displaystyle μ &&→&&(X,σ,μ^*) \end{array}
だいたい「拡張 μ^* 」が存在します。
(具体的には区間の長さとかのこと)
前測度の具体例
この「前測度」という概念は
「初等的(直感的)な測度」の一般化なので
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
基本的には
「区間の長さ」や「区間塊の長さ」
「ジョルダン測度」なんかを意味します。
厳密な定義
これは「集合半環 \mathrm{semiRing} 」
「集合環 \mathrm{Ring} 」「集合体 \mathrm{Field} 」という
非常に抽象的な集合の上で定義されていて
\begin{array}{llllll} \displaystyle \begin{array}{rrr} \displaystyle ∅&≠&\mathrm{Ring} \\ \\ A\setminus B&\in&\mathrm{Ring} \\ \\ A∪B&\in&\mathrm{Ring} \end{array} &&&&\begin{array}{rrr} \displaystyle ∅&∈&\mathrm{Ring} \\ \\ A∩ B&\in&\mathrm{Ring} \end{array} \end{array}
\begin{array}{ccccc} A\setminus B &&→&&(A^c∪B)^c \\ \\ \displaystyle \mathrm{Ring}&&←&&\mathrm{Field} \\ \\ \{∅\} && &&\{∅,X\} \\ \\ \{∅,\{a\}\} && && \{∅,\{a\},\{b\},\{a,b\}\} \end{array}
「測度空間」上で定義されていないので
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}}&:& \mathrm{Ring} &→&[0,\infty] \end{array}
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}}(∅)&=&0 \end{array}
\begin{array}{ccccccc} \begin{array}{ccc} i≠j ⇒ A_i∩A_j=∅ \\ \\ A_1,A_2,...,A_n,... \in \mathrm{Ring} \\ \\ \displaystyle\bigcup_{n=1}^{\infty}A_n\in \mathrm{Ring} \end{array}&→&\displaystyle μ_{\mathrm{pre}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{pre}}(A_n) \end{array}
上記の定義の形自体は
「測度の定義」とまったく同じなんですが
厳密には
「測度」とは異なる概念になります。
(可測空間上の測度の条件として機能する)
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}}&:& \mathrm{Ring} &→&[0,\infty] \end{array}
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{pre}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{pre}}(A_n) \end{array}
\begin{array}{ccc} \mathrm{disjoint} &:=& \left( \begin{array}{c} i≠j \\ ↓ \\ A_i∩A_j=∅ \end{array} \right) \end{array}
また当然ですが
「正の実数」「完全加法性」が条件に来るので
「全ての関数(集合関数)」を含むわけではありません。
集合体(有限加法族)と完全加法族
補足しておくと
「集合環から完全加法族を形成する」場合
\begin{array}{ccc} \displaystyle \mathrm{Ring}&&\mathrm{Field} \\ \\ A\setminus B && A^c \end{array}
「集合環」「集合体」の明確な違いである
「補集合」を結果的に含むことになるため
(集合体は差集合も含む)
\begin{array}{ccc} \displaystyle \mathrm{Ring} &→&σ(\mathrm{Ring}) \\ \\ \{∅\} && \{∅,X\} \\ \\ \{∅,\{a\}\} && \{∅,\{a\},\{b\},\{a,b\}\} \\ \\ \\ \mathrm{Field} &→&σ(\mathrm{Field}) \\ \\ A\setminus B \,\, A^c && A\setminus B \,\, A^c \end{array}
「集合体から」形成する場合と
「形成される完全加法族」の中身は同じになります。
(集合環は全体 X の帰属を強制してないだけ)
集合環と集合体の違い
どちらで定義しても良い。
これは事実なんですが
\begin{array}{llllll} \displaystyle A∈\mathrm{Field}&&→&&A^c∈\mathrm{Field} \end{array}
「集合体」で定義する場合の注意点として
例えば「区間」を考える時
\begin{array}{llllll} \displaystyle [a,b)∈\mathrm{Field}&&→&&(-\infty,a)∪[b,\infty)∈\mathrm{Field} \end{array}
「補集合」を含むことになるので
\begin{array}{ccl} [a,\infty) &=& \{ x\in R \mid a<x<\infty \} \\ \\ (-\infty,b) &=& \{ x\in R \mid -\infty<x<b \} \end{array}
「実数全体」を「区間」で考えるなら
\begin{array}{lcc} μ(R)&=&\infty \\ \\ μ\Bigl( [a,\infty) \Bigr)&=&\infty \\ \\ μ\Bigl( (-\infty,b) \Bigr)&=&\infty \end{array}
「無限区間」や
\begin{array}{ccc} \infty-\infty &&\mathrm{indefinite} \\ \\ \infty \times 0 && \mathrm{indefinite} \\ \\ \infty / \infty &&\mathrm{indefinite} \end{array}
「不定形」を考慮するために必要な
\begin{array}{lcr} \infty +\infty&=&\infty \\ \\ \infty +r&=&\infty \\ \\ \\ \infty -r&=&\infty \\ \\ r-\infty&=&-\infty \end{array}
\begin{array}{lcr} \infty \times \infty&=& \infty \\ \\ \infty \times r&=& \infty && 0<r \\ \\ \infty \times (-\infty)&=& -\infty \\ \\ \infty \times r&=& -\infty && r<0 \end{array}
\begin{array}{ccr} \infty / r&=& \infty && 0<r \\ \\ \infty / r&=& -\infty && r<0 \\ \\ r/\infty &=&0 &&-\infty<r <\infty \end{array}
「無限の演算規則」を考える必要が出てきます。
(集合環では無限区間を考えなくて良い)
これが本質的な違いで
\begin{array}{ccc} A^c &=& X\setminus A \end{array}
\begin{array}{cccc} X&\not\in& \mathrm{Ring} &&〇 \\ \\ X&\in& \mathrm{Ring} &&〇 \end{array}
「集合環 \mathrm{Ring} 」は
「全体 X 」を考えなくて良いので
「前測度」を「集合環」上で定義する場合
「測度が無限になる場合」を考える必要がなくなります。
集合半環での定義が最も抽象的
「集合体」より抽象的な「集合環」という集合族は
「差集合」「和集合」について閉じていますが
\begin{array}{llllll} \mathrm{Interval} &=& \left\{ [a,b) \mid -\infty<a≤b<\infty \right\} \end{array}
測度の基礎となる「基本集合」
これを定義する「区間 [a,b) 」は
\begin{array}{llllll} [a,b)∩[c,d) &\in&\mathrm{Interval} \end{array}
「交叉(共通部分)」については閉じていますが
(交叉で閉じてるやつは 乗法族 πシステム と呼ばれる)
\begin{array}{llllll} \displaystyle [0,1) ∪ [2,3) &\not\in&\mathrm{Interval} \\ \\ \displaystyle [0,3)\setminus [1,2) &\not\in&\mathrm{Interval} \end{array}
「差集合」「和集合」については閉じていません。
しかし「区間の長さ μ 」は
直感的にはかなり「前測度」なので
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
\begin{array}{llllll} 0&≤& \displaystyle μ\Bigl( [a,b) \Bigr)&<&\infty \end{array}
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ\left(\bigcup_{n=1}^{\infty}I_n\right) =\sum_{n=1}^{\infty}μ(I_n) \end{array}
これも「前測度」としたいです。
(区間の長さは完全加法的集合関数になる)
前測度かどうかの確認方法
これは基本的には
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}}&:& \mathrm{Ring} &→&[0,\infty] \end{array}
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{pre}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{pre}}(A_n) \end{array}
これらを満たすかどうかで判断されます。
「集合半環 \mathrm{semiRing} 」上であるか
「集合環 \mathrm{Ring} 」上であるか
「集合体 \mathrm{Field} 」上であるか
この辺りについては
正直あまり意識されません。
(だいたい前提で定義されているので)
ジョルダン測度は厳密には測度ではない
「測度」は「可測集合」上で定義できて
「測度空間」を形成する
\begin{array}{llllll} \displaystyle \begin{array}{cc} \displaystyle (X,σ_X) \\ \\ μ \end{array}&→&(X,σ_X,μ) \end{array}
とまあそういう形で定義されていますが
実は「完全加法族」が
「ジョルダン非可測な集合」を含むので
\begin{array}{llllll} \displaystyle S_{\mathrm{Jordan \,\, non-measurable}}&⊂&σ \end{array}
「ジョルダン測度(ジョルダン容積)」は
「可測空間」上では定義できません。
ジョルダン測度の厳密な定義
確認しておくと
「ジョルダン測度 μ_{\mathrm{Jordan}} 」は
\begin{array}{llllll}μ_{\mathrm{Jordan}}^{\mathrm{inner}}(A) &=& \displaystyle μ_{\mathrm{Jordan}}(A)&=&μ_{\mathrm{Jordan}}^{\mathrm{outer}}(A) \end{array}
「外容量・内容量」が『一致した時の値』として
(考え方は極限の右極限と左極限)
\begin{array}{llllll} \displaystyle S&=&\displaystyle \bigcup_{n=1}^{\infty}I_n \end{array}
\begin{array}{ccccl} A⊂S &&→&& \displaystyle μ_{\mathrm{Jordan}}^{\mathrm{outer}}(A)=\displaystyle\inf \left\{ μ_{\mathrm{base}}(S) \right\} \\ \\ S ⊂ A &&→&& μ_{\mathrm{Jordan}}^{\mathrm{inner}}(A)=\displaystyle\sup \left\{ μ_{\mathrm{base}}(S) \right\} \end{array}
\begin{array}{ccc} \displaystyle I&=&[a,b) \\ \\ μ_{\mathrm{base}}(I)&=&b-a \\ \\ I_X \times I_Y&=&[a_x,b_x)\times [a_y,b_y) \\ \\ μ_{\mathrm{base}}(I_X\times I_Y)&=&(b_x-a_x)(b_y-a_y) \end{array}
「基本集合」をベースに
このような形で定義されています。
(完全加法族では定義されていない)
「図形 S 」が「区間の長さ μ_{\mathrm{base}} 」で測れるのか
この点については疑問かもしれませんが
\begin{array}{llllll} \displaystyle \int_{a}^{b}f(x)\,dx &=&F(b)-F(a) \end{array}
これは「積分」を理解してれば
これが「区間 [F(a),F(b)) の長さ」と同一になるので
問題ないということは分かると思います。
基本集合と図形
「ジョルダン測度」の最小単位に来る
「基本集合」という概念は
\{ [a,b) ⊂ R \mid -\infty<a≤b<\infty \}
この「有界な区間 [a,b) 」で定義されていて
\begin{array}{llllll} \displaystyle F&=&\displaystyle \bigcup_{n=1}^{k}[a_n,b_n) \end{array}
「求めたい図形の全体 A を囲む図形」は
「区間塊 F 」で定義されています。
(平面では矩形塊などと呼ばれる)
大きさを得たい図形の定義
これがちょっと意味わかんないかもですが
\begin{array}{ccc} [0,1) &⊂& (-1,1) \\ \\ \displaystyle S_{\mathrm{bound}}&⊂&\mathrm{Ball}(0,r) \end{array}
「求めたい図形 A 」は
\begin{array}{llllll} \displaystyle \mathrm{Ball}(0,r)&=&\{ x∈R \mid |x|<r \} \\ \\ \mathrm{Ball}(0,r)&=&\{ (x,y)∈R^2 \mid \sqrt{x^2+y^2}<r \} \end{array}
こういう集合で囲うことができる
「有界集合 S_{\mathrm{bound}} 」で定義されています。
区間塊による図形の近似
「近似図形 S 」を意味する
「基本集合の集まり(区間塊)」と
\begin{array}{ccc} \displaystyle I&=&[a,b) \\ \\ μ_{\mathrm{base}}(I)&=&b-a \\ \\ I_X \times I_Y&=&[a_x,b_x)\times [a_y,b_y) \\ \\ μ_{\mathrm{base}}(I_X\times I_Y)&=&(b_x-a_x)(b_y-a_y) \end{array}
「上限・下限の存在」から
\begin{array}{llllll} \displaystyle S&=&\displaystyle\bigcup_{n=1}^{\infty}I_n \end{array}
「ジョルダン測度」は
\begin{array}{ccccc} && A&⊂&S \\ \\ && μ_{\mathrm{Jordan}}(A) &≤&\displaystyle μ_{\mathrm{base}}(S) \\ \\ S&⊂&A \\ \\ \displaystyle μ_{\mathrm{base}}(S)&≤& μ_{\mathrm{Jordan}}(A) \end{array}
このような手順を経ることで
その大きさを定義しています。
ジョルダン可測と完全加法族
「ジョルダン外測度(外容量) μ_{\mathrm{Jordan}}^{\mathrm{outer}} 」
「ジョルダン内測度(内容量) μ_{\mathrm{Jordan}}^{\mathrm{inner}} 」
\begin{array}{llllll} \displaystyle S&=&\displaystyle \bigcup_{n=1}^{\infty}I_n \end{array}
\begin{array}{ccccl} A⊂S &&→&& \displaystyle μ_{\mathrm{Jordan}}^{\mathrm{outer}}(A)=\displaystyle\inf \left\{ μ_{\mathrm{base}}(S) \right\} \\ \\ S ⊂ A &&→&& μ_{\mathrm{Jordan}}^{\mathrm{inner}}(A)=\displaystyle\sup \left\{ μ_{\mathrm{base}}(S) \right\} \end{array}
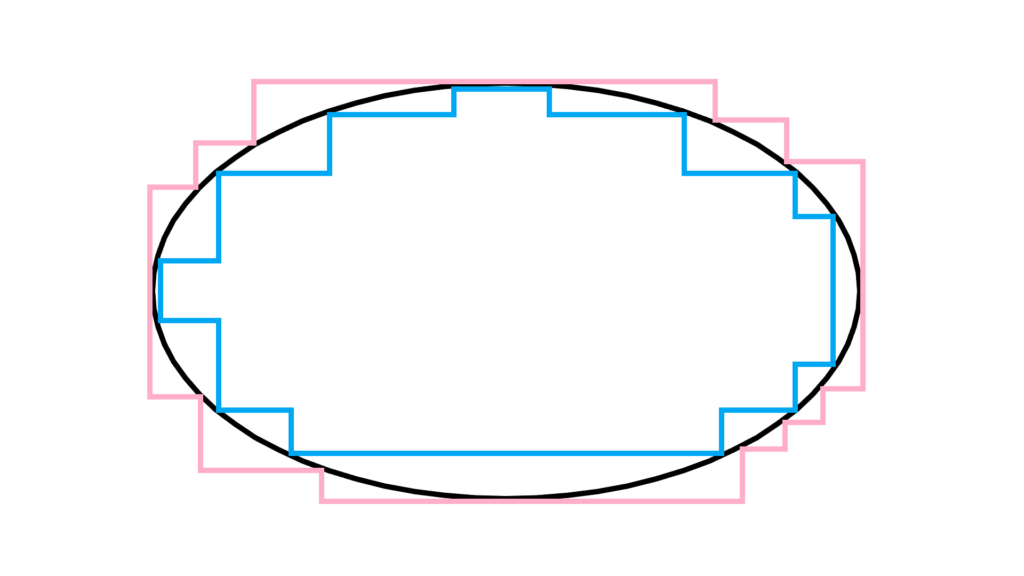
この一致により定義される
\begin{array}{llllll} μ_{\mathrm{Jordan}}^{\mathrm{inner}}(A)&=& μ_{\mathrm{Jordan}}(A) &=& μ_{\mathrm{Jordan}}^{\mathrm{outer}}(A) \end{array}
「ジョルダン可測」は
実はカバーできる範囲がわりと狭いです。
(直感的には特に問題ないくらい広い)
ジョルダン非可測な集合
例えば
「内測度が 0 になる(基本集合無し)」上に
「外測度は大きくなる」「稠密(ぎっしり)な集合」
\begin{array}{ccccc} \displaystyle \mathrm{Point}&&→&&\mathrm{Points} \\ \\ \{a\} &&→&& \displaystyle\bigcup \{a\} \end{array}
具体的には
「有理数全体 Q (点集合の無限和)」や
その「補集合 Q^c (無理数)」なんかは
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}\{q_n\} &=&Q &&∈σ \end{array}
\begin{array}{ccccc} \{\}&⊂&\{a\}&⊂&[a,a+ε) \\ \\ \displaystyle \{\}&⊂&Q&⊂&(-\infty,\infty) \\ \\ \{\}&⊂&Q∩[0,1)&⊂&[0,1) \end{array}
間違いなく
「完全加法族上で定義される集合」なのに
\begin{array}{ccc} μ_{\mathrm{Jordan}}^{\mathrm{inner}}(Q∩[0,1)) && μ_{\mathrm{Jordan}}^{\mathrm{outer}}(Q∩[0,1)) \\ \\ \displaystyle μ_{\mathrm{base}}(\{\}) &&μ_{\mathrm{base}}([0,1)) \\ \\ 0 &≠&1 \end{array}
「基本集合(区間)」が最小単位に来る以上
どうやっても不一致になるため
「ジョルダン非可測」になってしまいます。
ジョルダン非可測集合は完全加法族上に存在する
そしてこの
「完全加法族」上では
「ジョルダン可測ではない集合」が定義される
\begin{array}{llllll} \displaystyle \{q_1\},\{q_2\},...∈σ &&→&&\displaystyle\bigcup_{n=1}^{\infty}\{q_n\}∈σ \end{array}
という結果から
「ジョルダン測度」は
「完全加法族」で定義される
「可測空間」上では矛盾なく定義できない
つまり厳密には
「測度ではない」ということになります。
(「容積」「外容量」「内容量」呼びの由来はこれ)
ジョルダン測度は測度の基本操作
とはいえ
「ジョルダン測度」それ自体は非常に直感的です。
\begin{array}{llllll} \displaystyle μ_{\mathrm{Jordan}}\Bigl([a,b)\Bigr)&=&b-a \end{array}
そもそもが「測度」という概念の出発点ですし
ほとんどの場合で特に問題は発生しない上
「測度」もまた同様の操作を行っています。
なのでこれを「測度ではない」というのは
なんかちょっと違和感があるというか
考えれば考えるほど
これを「測度ではない」とするのは変な感じがします。
ジョルダン測度と前測度
ここで出てくるのが
「前測度」という概念で
\begin{array}{cccccccccc} \displaystyle σ&&→&& \mathrm{Field} &&→&&\mathrm{Ring} \\ \\ A^c \,\,\,\,\, \displaystyle\bigcup_{n=1}^{\infty}A_n &&→&& A^c \,\,\,\,\, A∪B &&→&& A\setminus B \,\,\,\,\, A∪B \end{array}
より縛りの緩い
「集合半環・集合環・集合体」上とすることで
「完全加法族」の本質的な役割を維持しながら
「点集合の無限和」を含んでしまうという
「完全加法族」の縛りを取り除き
\begin{array}{llllll} \displaystyle \{q_1\},\{q_2\},...∈σ &&→&&\displaystyle\bigcup_{n=1}^{\infty}\{q_n\}∈σ &&強制 \\ \\ \{q_1\},\{q_2\},...∈\mathrm{Ring} &&→&&\displaystyle\bigcup_{n=1}^{\infty}\{q_n\}∈\mathrm{Ring} &&任意 \end{array}
「ジョルダン非可測」な集合を
除外しても問題ないようにすることで
\begin{array}{llllll} \displaystyle μ_{\mathrm{Jordan}}(∅)&=&0 \end{array}
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &&→&&\displaystyle μ_{\mathrm{Jordan}}\left( \bigcup_{n=1}^{\infty}A_n \right)=\sum_{n=1}^{\infty}μ_{\mathrm{Jordan}}(A_n) \end{array}
「ジョルダン可測な集合」上のみで
「ジョルダン測度」を扱えるようにする
ということをこの「前測度」は実現しています。
ジョルダン測度は前測度である
順番的には
「ジョルダン測度」→「前測度の定義」なんですが
\begin{array}{cccc}&\mathrm{Generalize}& \\ \\ μ_{\mathrm{Jordan}} &\to& μ_{\mathrm{pre}} &&〇 \\ \\ \displaystyle μ_{\mathrm{Jordan}} &←& μ_{\mathrm{pre}} &&?\\ \\ &\mathrm{Proof}& \end{array}
この「ジョルダン測度」が
きちんと「前測度の定義」を満たすのか
この時点ではまだ分かっていないので
念のため、ここできちんと確認を行っておきます。
ジョルダン測度は前測度の定義を満たす
まず「前測度」ですが
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}}&:& \mathrm{Ring} &→&[0,\infty] \end{array}
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{pre}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{pre}}(A_n) \end{array}
そもそもの話
これは全ての測度の雛型です。
この条件を満たさない場合
そもそもそれは測度ではありません。
まあなので結論ははっきりしてるんですが
「前測度」の定義が正しいのか
まだ曖昧なので
\begin{array}{llllll} \displaystyle \begin{array}{cc} \displaystyle ∅≠\mathrm{Ring} \\ \\ A\setminus B \in \mathrm{Ring} \end{array} &→&∅\in\mathrm{Ring} \end{array}
とりあえず「集合環」を確認し
その上で定義される「ジョルダン測度」を見てみます。
ジョルダン測度の定義の確認
確認しておくと
\begin{array}{lll} \displaystyle I&=&[a,b) \\ \\ I_X\times I_Y &=&[a_x,b_x)\times [a_y,b_y) \end{array}
\begin{array}{llllll} \displaystyle μ_{\mathrm{base}}\Bigl( [a,b) \Bigr) &=&b-a \\ \\ μ_{\mathrm{base}}\Bigl( [a_x,b_x)\times [a_y,b_y) \Bigr)&=&(b_x -a_x)(b_y -a_y) \end{array}
基本集合と長さの定義がこれ
\begin{array}{llllll} \mathrm{Fig} &=& \displaystyle \bigcup_{n=1}^{\infty}I_n \end{array}
\mathrm{Fig} が A に限りなく近い形をした区間塊で
\begin{array}{ccccl} A⊂\mathrm{Fig} &&→&& \displaystyle μ_{\mathrm{Jordan}}^{\mathrm{outer}}(A)=\displaystyle\inf \left\{ μ_{\mathrm{base}}(\mathrm{Fig}) \right\} \\ \\ \displaystyle \mathrm{Fig} ⊂ A &&→&& μ_{\mathrm{Jordan}}^{\mathrm{inner}}(A)=\displaystyle\sup \left\{μ_{\mathrm{base}}(\mathrm{Fig}) \right\} \end{array}
「ジョルダン測度」は
基本的にこの形で定義されています。
\begin{array}{llllll} \displaystyle a<b &&→&&[a,b)≠∅ \\ \\ a\textcolor{skyblue}{≥}b &&→&&[a,b)=∅ \end{array}
また「基本集合」を定義する「区間」の定義より
これは必ずこうなるため
\begin{array}{llllll} [a,b) &&→&& \displaystyle a<b \end{array}
基本的に
この範囲以外を考える意味はありません。
(この範囲以外では測度 0 として話を進めていく)
空集合とジョルダン測度
「長さ」についての公理
(長さやその直積である面積は正の実数)
\begin{array}{llllll} 0 &≤& \displaystyle μ(A) \end{array}
「基本集合 I 」がベースになっている
この2つの事実から
\begin{array}{llllll} \displaystyle a\textcolor{skyblue}{≥}b &&→&&[a,b)=∅ \end{array}
\begin{array}{llllll} 0&≤& \displaystyle μ_{\mathrm{base}}(∅)&≤&μ_{\mathrm{base}}\Bigl( [a,a+ε) \Bigr) \end{array}
まず「空集合」については
このように「外容量」を定めれば
\begin{array}{llllll} \displaystyle \inf \left( μ_{\mathrm{base}}\Bigl( [a,a+ε) \Bigr) \right)&=&0 \end{array}
\begin{array}{llllll} \displaystyle μ_{\mathrm{base}}(∅)&=&0 \end{array}
このような自然な結論がすぐに得られます。
ジョルダン測度の定義域と終域
以上の事実を踏まえて
\begin{array}{llllll} μ_{\mathrm{base}}\Bigl([a,b)\Bigr)&=&b-a \\ \\ \displaystyle μ_{\mathrm{base}}\Bigl([a,b+ε)\Bigr) &=&b-a+ε \end{array}
「基本集合の測度」がこのようになる
ということを考えると
\begin{array}{llllll} \displaystyle μ_{\mathrm{base}}\Bigl([a,b)\Bigr)&≤&μ_{\mathrm{base}}\Bigl([a,b+ε)\Bigr) \\ \\ μ_{\mathrm{base}}\Bigl([a,b)\Bigr)&≤&μ_{\mathrm{base}}\Bigl([a,b+n)\Bigr) \end{array}
区間を適当に広くしていけば
こんな感じの区間を考えられることから
\begin{array}{llllll} \displaystyle μ_{\mathrm{base}}\Bigl( [a,b+p) \Bigr)≤μ_{\mathrm{base}}\Bigl([a,b+nq) \Bigr) &&\Bigl( 0<p,q \Bigr) \end{array}
「アルキメデスの原理」より
\begin{array}{llllll} \displaystyle \sup \left( μ_{\mathrm{base}}\Bigl( [a,b+nq) \Bigr) \right)&=&\infty \end{array}
「 b+nq 」は「非有界」となるため
「区間の大きさを好きにとれる」とするなら
「ジョルダン測度」の『像』の範囲は
\begin{array}{cccccc} \displaystyle 0&≤&μ_{\mathrm{base}}(A)&<&\infty \\ \\ && ↓ && \\ \\ 0&≤&μ_{\mathrm{Jordan}}(A)&<&\infty \end{array}
出来る限り広くとると
「非有界」の範囲にまで広げることができると言えます。
終域とジョルダン測度の像
再度確認しておくと
「前測度」の定義は
\begin{array}{llllll} \displaystyle μ_{\mathrm{pre}} &:& A &→& [0,\infty] \end{array}
こうです。
「終域」に「無限」が含まれています。
そして「終域 B 」の定義なんですが
\begin{array}{rcc} \displaystyle f(A)&⊂&B \\ \\ μ(A)&⊂&B \end{array}
これは「像 f(A) 」を
「全て内側に含んでいる」なら
なんでも「終域 B 」と言えるので
「ジョルダン測度」の「終域」は
\begin{array}{cccccc} μ_{\mathrm{Jordan}} &:& A &→& μ_{\mathrm{Jordan}}(A) \\ \\ && && ↓ && \\ \\ \displaystyle μ_{\mathrm{Jordan}} &:& A &→& [0,\infty) \\ \\ && && ↓ && \\ \\ μ_{\mathrm{Jordan}} &:& A &→& [0,\infty] \end{array}
「最大の範囲 0≤μ(A)<\infty 」が
全て内側に来る以上
このようにできると言えます。
ジョルダン測度と無限和
「 \mathrm{disjoint} の条件」から
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{pre}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{pre}}(A_n) \end{array}
この結論が得られるかどうか
これは「ジョルダンによる面積の定義」や
「区間・区間塊の長さ」の定義より
直感的には明らかなんですが
\begin{array}{llllll} A∩B=∅ &&→&& \displaystyle μ(A∪B)=μ(A)+μ(B) \end{array}
「無限和」に関してはどうなのか
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{Jordan}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{Jordan}}(A_n) \end{array}
ちょっと怪しいので
この辺り、きちんと確認しておきます。
ジョルダン測度と有限和
まず「面積の定義」について再確認しておくと
\begin{array}{llllll} A∩B=∅ &&→&& \displaystyle μ(A∪B)=μ(A)+μ(B) \end{array}
こうであり
\begin{array}{llllll} A∩B=∅ &&→&& |A∪B|=|A|+|B| \end{array}
これを満たすように定義された
「基本集合の長さ」もまたこうなります。
ということは
「非交和 \mathrm{disjoint} 」を条件とする
「加法性」については確実に満たされているので
\begin{array}{llllll} \displaystyle μ\Bigl((A∪B)∪C\Bigr)=μ(A)+μ(B)+μ(C) \end{array}
\begin{array}{llllll} \displaystyle μ\left( \bigcup_{n=1}^{k}A_n \right) &=&\displaystyle \sum_{n=1}^{k} μ(A_n) \end{array}
こうなるのは確実です。
(そもそも区間の長さは有限加法的)
念のため確認しておくと
\begin{array}{llllll} \displaystyle μ\left( \left( \bigcup_{n=1}^{k}A_n \right)∪A_{k+1} \right) &=&\displaystyle \left(\sum_{n=1}^{k} μ(A_n) \right) +μ(A_{k+1}) \\ \\ \displaystyle μ\left( \bigcup_{n=1}^{k+1}A_n \right) &=&\displaystyle \sum_{n=1}^{k+1} μ(A_n) \end{array}
確実にこうなると言えるので
「数学的帰納法」を考えると
「全ての自然数 k で成立する」と言えることから
\begin{array}{llllll} \displaystyle μ_{\mathrm{Jordan}}\left( \bigcup_{n=1}^{k}A_n \right) &=&\displaystyle \sum_{n=1}^{k} μ_{\mathrm{Jordan}}(A_n) \end{array}
「非交和 \mathrm{disjoint} 」の条件下では
必ずこうなると言えます。
ジョルダン可測な無限和
「有理数全体」のように
「全ての無限和」では
「ジョルダン可測」の条件を満たすことはできません。
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}A_n&=&X \end{array}
しかし「ジョルダン可測」な「無限和」は
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty} \left[ a-\frac{1}{n},b \right)&=&(a,b) \end{array}
こういったものが確かに存在するため
これで「無限和」に関して
「ジョルダン可測な集合の存在」が示されます。
また「 \mathrm{disjoint} の条件」を満たすものとして
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty} [n-1,n) &=&[0,\infty) \end{array}
こういった無限和も考えることができ
\begin{array}{llllll} \displaystyle \sum_{k=1}^{n} \left(\frac{1}{2} \right)^k &=& \displaystyle \frac{\frac{1}{2}-\left( \frac{1}{2} \right)^n }{1-\frac{1}{2}} \end{array}
\begin{array}{llllll}\displaystyle \left[ 0,\frac{1}{2} \right) ∪ \left[ \frac{1}{2},\frac{1}{2}+\frac{1}{4} \right) ∪ \left[ \frac{1}{2}+\frac{1}{4},\frac{1}{2}+\frac{1}{4}+\frac{1}{8} \right)∪ \cdots &=& [0,1) \\ \\ \displaystyle \bigcup_{n=1}^{\infty} \left[ -\left(\frac{1}{2}\right)^n + \sum_{k=1}^{n} \left(\frac{1}{2} \right)^k , \sum_{k=1}^{n} \left(\frac{1}{2} \right)^k \right) &=&[0,1) \end{array}
「有界集合」の範囲では
こういったものも考えることができるため
\begin{array}{llllll} \displaystyle μ_{\mathrm{Jordan}}\left(\bigcup_{n=1}^{\infty}A_n \right)&∈&R_+ \end{array}
「ジョルダン可測な無限和」は
確実に存在すると言えます。
ジョルダン測度と集合環と無限和
以上のことから
「完全加法族」上では
↓ は必ず成立するとは言えませんが
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{Jordan}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{Jordan}}(A_n) \end{array}
「無限和」を
強制ではなく任意に含む「集合環」上では
(区間塊は集合環であることを前提に話を進めてます)
\begin{array}{llllll}\displaystyle \left[ 0,\frac{1}{2} \right) ∪ \left[ \frac{1}{2},\frac{1}{2}+\frac{1}{4} \right) ∪ \left[ \frac{1}{2}+\frac{1}{4},\frac{1}{2}+\frac{1}{4}+\frac{1}{8} \right)∪ \cdots &=& [0,1) \end{array}
「ジョルダン可測な無限和が存在する」ことから
成立し得ると言えるので
\begin{array}{llllll} \displaystyle \mathrm{disjoint}&→&\displaystyle μ_{\mathrm{Jordan}}\left(\bigcup_{n=1}^{\infty}A_n\right) =\sum_{n=1}^{\infty}μ_{\mathrm{Jordan}}(A_n) \end{array}
「基本集合の長さが完全加法的である」ことより
「集合環」上でこれは成立すると言えます。
(非可測なものは考えなくて良い)
以上
「集合環」上で以下が成り立つので
\begin{array}{llllll} \displaystyle μ_{\mathrm{Jordan}} &:& A &→& [0,\infty] \end{array}
\begin{array}{llllll} \mathrm{disjoint} &&→&& \displaystyle μ_{\mathrm{Jordan}}\left( \bigcup_{n=1}^{\infty}A_n \right) =\displaystyle \sum_{n=1}^{\infty} μ_{\mathrm{Jordan}}(A_n) \end{array}
「ジョルダン測度」は
「前測度」の定義を満たすと言えます。
