|| 次元を増やす感じの操作
「線」から「面」「立体」を作る時のやつ
本質的には「組」を考えるためのものです。
スポンサーリンク
目次
測度「長さとか面積とか体積のこと」
直積測度「次元を増やす感覚を形式化したもの」
直積測度空間「直積測度を定義するちょっと面倒なやつ」
直積集合「デカルト積を使うとできる集合のこと」
長方形「線×線 の直積によって定義される」
可測長方形「可測空間上の長方形のこと」
積分「厳密には直積測度によって定義される」
コルモゴロフの拡張定理「直積は無限回してOK」
直積測度 Product Measure
|| 測度の掛け算的な操作の話
以下の条件を満たす μ_{X\times Y} が「直積測度」です
\begin{array}{llllll} μ_{X\times Y}&=&μ_X\times μ_Y \\ \\ μ_{X\times Y}&=&μ_X\otimes μ_Y \end{array}
\begin{array}{llllll} \displaystyle I_X&∈&σ_X \\ \\ I_Y&∈&σ_Y \end{array}
\begin{array}{llllll} \displaystyle μ_{X\times Y}(I_X\times I_Y)&=&μ_X(I_X)μ_Y(I_Y) \end{array}
「測度空間」の「次元を増やす」感覚として
\begin{array}{ccccc} 長さ&→&面積 \\ \\ μ(I) &→&μ(I_X)μ(I_Y) \end{array}
これはこのように定義されています。
(測度空間 (X,σ_X,μ_X) \,\, (Y,σ_Y,μ_Y) 上の話)
直積測度空間 Space
|| 直積測度を定義する上でのあれこれ
「直積」操作の具体的な中身の話
\begin{array}{ccccc} \begin{array}{l} (X,σ_X,μ_X) \\ \\ (X,σ_Y,μ_Y) \end{array} &&→&&\displaystyle \Bigl( X\times Y, σ_X \otimes σ_Y, μ_X \times μ_Y \Bigr) \end{array}
よく分からん記号で定義されてますが
これについては
\begin{array}{ccc} \mathrm{Borel}(X)&=& σ\Bigl( O(X) \Bigr) \\ \\ \mathrm{Borel}(R)&=& σ\Bigl( O(R) \Bigr) \end{array}
\begin{array}{lcl} R&→&\displaystyle \left( R,σ\Bigl( O(R) \Bigr),μ \right) \\ \\ R^2 &→&\displaystyle \left( R\times R,σ\Bigl( O(R) \Bigr)\otimes σ\Bigl( O(R) \Bigr),μ \times μ \right) \end{array}
直感的に理解して大丈夫です。
( \mathrm{Borel}(R) はボレル集合族)
デカルト積 Direct Product
「ペア(対・組)を作る」操作のことで
\begin{array}{llllll} X\times Y &=&\{ (x,y) \mid x∈X ∧ y∈Y \} \\ \\ \displaystyle \prod_{k=1}^{n}X_n &=& \{ (x_1,x_2,...,x_n) \mid x_1∈X_1 ∧ \cdots ∧ x_n∈X_n \} \end{array}
\begin{array}{ccl} \displaystyle \prod_{k=1}^{n}X_n &=&X_1\times X_2\times \cdots \times X_n \\ \\ X^n &=&X\times X \times \cdots \times X \end{array}
分かりやすく「次元を増やす」感覚を表現します。
(プログラムで使う配列のあれ)
具体的には ↓ みたいな感じ。
\begin{array}{ccl} A&=&\{a_1,a_2\} \\ \\ B&=&\{b_1,b_2,b_3\} \end{array}
\begin{array}{llllll} A\times B &=&\displaystyle \left\{ \begin{array}{ccc} (a_1,b_1)&(a_1,b_2)&(a_1,b_3) \\ \\ (a_2,b_1)&(a_2,b_2)&(a_2,b_3) \end{array} \right\} \end{array}
これが「連続」となると
\begin{array}{llllll} R\times R &=&\{ (x,y) \mid x∈R ∧ y∈R \} \end{array}
例えばこれは
「平面内の全ての座標」を意味します。
(実際には解像度の範囲の座標を扱うことが多い)
他にも
\begin{array}{ccl} \mathrm{Suit}&=&\{\clubsuit,\diamondsuit,\heartsuit,\spadesuit\} \\ \\ \mathrm{Rank}&=&\{A,2,3,4,5,6,7,8,9,10,J,Q,K\} \end{array}
\begin{array}{llllll} \mathrm{Suit}\times \mathrm{Rank} &=&\displaystyle \left\{ \begin{array}{ccccc} (\clubsuit,A)&(\clubsuit,2)&\cdots&(\clubsuit,Q)&(\clubsuit,K) \\ \\ (\diamondsuit,A)&(\diamondsuit,2)&\cdots&(\diamondsuit,Q)&(\diamondsuit,K) \\ \\ (\heartsuit,A)&(\heartsuit,2)&\cdots&(\heartsuit,Q)&(\heartsuit,K) \\ \\ (\spadesuit,A)&(\spadesuit,2)&\cdots&(\spadesuit,Q)&(\spadesuit,K) \end{array} \right\} \end{array}
単純にこういった「ペア」を考える時
集合同士の「直積」はこんな感じになります。
テンソル積 Tensor Product
「テンソル」に定義される「積」のこと
\begin{array}{ccc} \displaystyle\left(\begin{array}{l} a_1 \\ \\ a_2 \\ \\ a_3 \end{array} \right) \otimes \left(\begin{array}{ccc} b_1&b_2&b_3 \end{array} \right) &=& \displaystyle \left( \begin{array}{ccc} a_1b_1 & a_1b_2 & a_1b_3 \\ \\ a_2b_1 & a_2b_2 & a_2b_3 \\ \\ a_3b_1 & a_3b_2 & a_3b_3 \end{array} \right) \end{array}
これはこんな感じになるんですが
(ここでは全ての区間でこれをやる感じ)
「完全加法族の積 σ_X\otimes σ_Y 」の中身は
\begin{array}{ccc} [a_x,b_x)\times [a_y,b_y) &\in&σ_X\otimes σ_Y \end{array}
こんな感じになる。
\begin{array}{ccc} [0,1)&→&\begin{array}{c} [0,1)\times [0,1) \\ \\ [0,1)\times [0,2) \\ \\ [0,1)\times [0,3) \\ \\ \vdots \end{array} \end{array}
この記事ではこれだけ分かっていれば十分です。
(簡単に説明できないので詳細はテンソルの記事で)
直積測度空間の具体例
これは「統計」で「サンプル」を扱う場合など
本当にいろいろあるんですが
「連続」となると
\begin{array}{ccccc} R\times R &→&[0,1)\times [0,1) \\ \\ && [0,1)\times [0,1) &→& \{(0,0),(0,1),\cdots\} \end{array}
だいたいこれしか使われず
他のを見ることはほとんどありません。
直積集合 Product Set
|| デカルト積で定義された組の集合
「直積」操作でできる集合のこと
\begin{array}{llllll} X\times Y &=&\{ (x,y) \mid x∈X ∧ y∈Y \} \\ \\ \displaystyle \prod_{k=1}^{n}X_n &=& \{ (x_1,x_2,...,x_n) \mid x_1∈X_1 ∧ \cdots ∧ x_n∈X_n \} \end{array}
「組・対」を要素に持っていて
例えば「対(2つの組)」は
\begin{array}{ccc} (a,b)&=&\displaystyle \Bigl\{ \{a\} , \{a,b\} \Bigr\} \\ \\ (a,b)&=&\displaystyle \Bigl\{ \{0,a\} , \{1,b\} \Bigr\} \end{array}
このような形で定義されています。
(こうすると順序対になっていろいろ便利)
\begin{array}{cclcl} 0\text{-}\mathrm{tuple} && ∅ \\ \\ 2\text{-}\mathrm{tuple} && (a_1,a_2)&=&\displaystyle \Bigl\{ \{a_1\} , \{a_1,a_2\} \Bigr\} \\ \\ n\text{-}\mathrm{tuple} && (a_1,a_2,...,a_n)&=&\displaystyle \Bigl\{ \{(a_1,...,a_{n-1})\} , \{ (a_1,...,a_{n-1}),a_{n}\} \Bigr\} \end{array}
ちなみに「 n-組」はこんな感じです。
空集合と直積集合
これについては
\begin{array}{ccccc} X\times ∅ &=&\{ (x,y) \mid x∈X ∧ y∈∅ \} \\ \\ &=&∅ \\ \\ \\ ∅\times Y &=&\{ (x,y) \mid x∈∅ ∧ y∈Y \} \\ \\ &=&∅ \end{array}
「直積集合」の定義から
\begin{array}{ccc} \displaystyle X \times ∅&=& ∅ \times Y \end{array}
このようになることが分かります。
またこの結果から
\begin{array}{llllll} \displaystyle μ_X\times μ_Y(X \times ∅)&=&μ_X(X) μ_Y(∅) \\ \\ μ_X\times μ_Y(∅ \times Y)&=&μ_X(∅) μ_Y(Y) \end{array}
「直積測度」で「空集合」を測る場合
\begin{array}{ccc} μ_X\times μ_Y(∅)&=&0 \end{array}
必ずこのようになることも分かります。
直積集合と演算
「あらゆる集合」は
\begin{array}{llllll} A&&→&&\{n\}∪[a,b)∪\cdots \\ \\ A\times B &&→&& \{(a,b)\}∪[a_1,b_1)\times [a_2,b_2)∪\cdots \end{array}
「シンプルな集合」に分解できる
(点・直線・平面など)
この事実を前提に
「直積」という操作について考えると
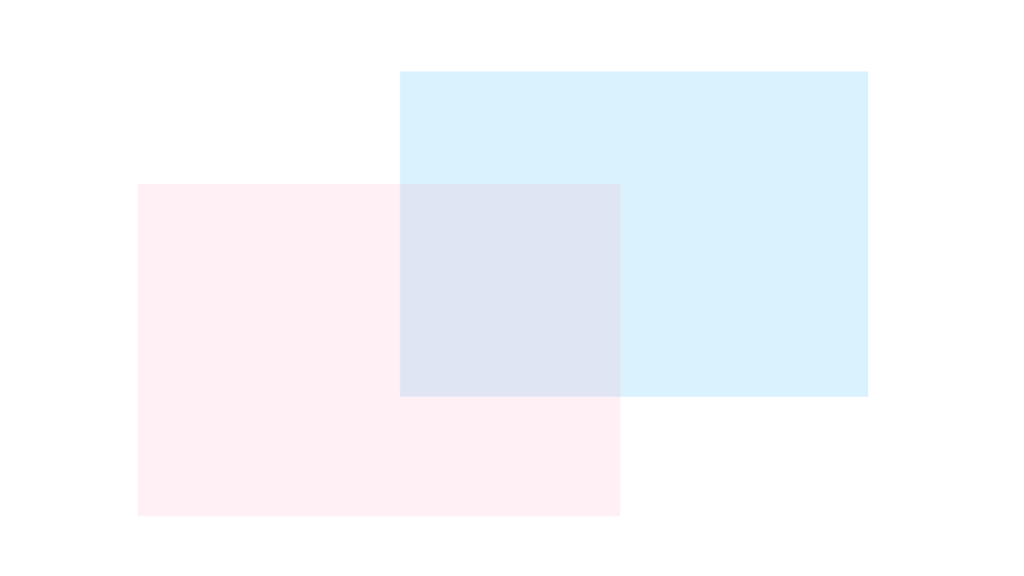
画像から分かる通り
\begin{array}{ccc} (\textcolor{pink}{X_1\times Y_1})∩(\textcolor{skyblue}{X_2\times Y_2}) &=&(X_1∩X_2)\times (Y_1∩Y_2) \\ \\ (\textcolor{pink}{X_1\times Y_1})∪(\textcolor{skyblue}{X_2\times Y_2}) &⊂&(X_1∪X_2)\times (Y_1∪Y_2) \end{array}
こういった性質がある
ということが分かります。

\begin{array}{ccc} (\textcolor{pink}{X_1\times Y_1})∩(\textcolor{skyblue}{X_2\times Y_2}) &=&(X_1∩X_2)\times (Y_1∩Y_2) && 〇 \\ \\ (\textcolor{pink}{X_1\times Y_1})∪(\textcolor{skyblue}{X_2\times Y_2}) &\textcolor{yellow}{=}&(X_1∪X_2)\times (Y_1∪Y_2) && × \end{array}
ただ、これらの性質は
視覚的には分かりやすいですが

\begin{array}{llllll} (\textcolor{steelblue}{X^c \times Y^c}) &⊂& (X\times Y)^c \\ \\ (\textcolor{steelblue}{X^c \times Y^c})∪(\textcolor{yellowgreen}{X \times Y^c})∪(\textcolor{green}{X^c \times Y}) &=& (X\times Y)^c \end{array}
数式を見るだけでは
\begin{array}{ccc} (X\times Y)^c \setminus (\textcolor{steelblue}{X^c \times Y^c})&=&(\textcolor{yellowgreen}{X \times Y^c})∪(\textcolor{green}{X^c \times Y}) \end{array}
「隙間の集合」が実感し辛いので
直感的には扱い辛いです。
特に「和集合」については

\begin{array}{ccc} (\textcolor{pink}{X_1\times Y_1})∪(\textcolor{skyblue}{X_2\times Y_2}) &⊂&(X_1∪X_2)\times (Y_1∪Y_2) \end{array}
隙間となる「2つの白い長方形」が
\begin{array}{llllll} (X_2\setminus X_1)\times (Y_1\setminus Y_2) \\ \\ (X_1\setminus X_2)\times (Y_2\setminus Y_1) \end{array}
こうなるので
数式からではよく分かりません。
点と直積集合の演算
↑ は「長方形(枠)」で考えましたが
これは「点」で考えても同様の結果になります。
\begin{array}{ccc} \{0,1\}\times \{0,1\} &=& \{ (0,0),(0,1),(1,0),(1,1) \} \end{array}
確認のために
例えばこれを使って「補集合」を考えると
\begin{array}{ccc} \Bigl( \{(0,0)\} \Bigr)^c &=&\{ (0,1),(1,0),(1,1) \} \\ \\ \Bigl( \{0\}\times \{0\} \Bigr)^c &=&\Bigl( \{0\}^c\times \{0\}^c \Bigr)∪\Bigl( \{0\}\times \{0\}^c \Bigr)∪\Bigl( \{0\}^c\times \{0\} \Bigr) \end{array}
考えてみれば当然ではありますが
\begin{array}{ccc} (\textcolor{steelblue}{X^c \times Y^c})∪(\textcolor{yellowgreen}{X \times Y^c})∪(\textcolor{green}{X^c \times Y}) &=& (X\times Y)^c \end{array}

結果は同じです。
(他の操作も同じ)
演算の証明手順
少し納得いかない部分があると思うので
ここで「分配法則」の証明を紹介しておきます。
\begin{array}{ccl} X \times (Y_1∪Y_2) &=& \{ (x,y) \mid x \in X ∧ y \in Y_1∪Y_2 \} \\ \\ &=&\{ (x,y) \mid x \in X ∧ (y \in Y_1∨ y \in Y_2) \} \\ \\ \\ (X\times Y_1)∪(X\times Y_2) &=&\{ (x,y) \mid x \in X ∧ y \in Y_1 \} ∪ \{ (x,y) \mid x \in X ∧ y \in Y_2 \} \\ \\ &=& \{ (x,y) \mid (x \in X ∧ y \in Y_1)∨(x \in X ∧ y \in Y_2) \} \end{array}
\begin{array}{ccc} A ∧ (B∨C) &=& (A ∧ B)∨( A∧C ) \\ \\ x \in X ∧ (y \in Y_1∨ y \in Y_2) &=& (x \in X ∧ y \in Y_1)∨(x \in X ∧ y \in Y_2) \end{array}
見て分かると思いますが
これは基本的に「集合」の話です。
\begin{array}{ccc} (\textcolor{steelblue}{X^c \times Y^c})∪(\textcolor{yellowgreen}{X \times Y^c})∪(\textcolor{green}{X^c \times Y}) &=& (X\times Y)^c \end{array}
なのでこれらを示す場合も
証明は ↑ みたいな感じになります。
長方形 Rectangle
|| 面積を定義する最小単位
「図形」「集合」「区間」「面積の定義」から
\begin{array}{llllll} \displaystyle \mathrm{Rect}&⊂&X\times Y \end{array}
「長方形 \mathrm{Rect} 」は
\begin{array}{llllll} \displaystyle I_X&⊂&X \\ \\ I_Y&⊂&Y \end{array}
「区間 I_X,I_Y 」の「直積」として
\begin{array}{llllll} \displaystyle \mathrm{Rect}&=&I_X \times I_Y \\ \\ &=& \{ (x,y) \mid x∈I_X ∧ y∈I_Y \} \end{array}
「測度論」的には
このような形で定義されています。
(点を意味する座標 (x,y) の集合)
可測長方形 Measurable Rectangle
|| そのまま可測な長方形(集合)のこと
「面積を求めることができる長方形」のこと
「長さ」を定める「区間」に相当するものになります。
\begin{array}{cccc} 長方形の面積&=&底辺×高さ \\ \\ \displaystyle |\mathrm{Rect}| &=& μ_X(I_X)μ_Y(I_Y) \end{array}
「可測である」という条件が付いただけで
\begin{array}{llllll} \displaystyle I_X&∈&σ_X \\ \\ I_Y&∈&σ_Y \end{array}
基本的には「長方形」の定義と同様です。
可測長方形と直積集合
「直積測度」を考える時
「直積集合」の雛型となるのが
\begin{array}{ccc} \mathrm{Rect}&=&I_X\times I_Y \end{array}
この「可測長方形 \mathrm{Rect} 」で
\begin{array}{ccc} μ_{X\times Y}(\mathrm{Rect})&=&μ_X(I_X)μ_Y(I_Y) \end{array}
こいつは非常にシンプルですから
\begin{array}{llllll} μ_{X\times Y}(\mathrm{Rect}_1∪\mathrm{Rect}_2)&≤&μ_{X\times Y}(\mathrm{Rect}_1)+μ_{X\times Y}(\mathrm{Rect}_2) \end{array}
「直積測度」の性質について
分かりやすいイメージの根拠になってくれます。
積分 Integral
|| 測度の一種として定義できる
「連続」版の「面積」を求める操作
\begin{array}{lcc} \displaystyle \int_{a}^{b} f(x) \, dx&=&F(b)-F(a) \\ \\ \displaystyle \int_{[a,b)} f(x) \, dx&=&F(b)-F(a) \end{array}
「定義関数」の「積分」を使って
( X は実数全体などの全体を意味する集合)
\begin{array}{ccc} 1_D(x) &=&\displaystyle \left\{ \begin{array}{ccl} 1 &&x\in D \\ \\ 0 &&x\not\in D \end{array} \right. \\ \\ \displaystyle \int_{X} 1_D(x) \,dx &=&μ(D) \end{array}
以下のように考えると
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle φ_n(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
\begin{array}{ccccl} φ_n(x) &≤& f(x) &=& \displaystyle \lim_{n\to\infty} φ_n(x) \\ \\ && &=&\displaystyle \lim_{n\to\infty} \sum_{k=1}^{n}a_k1_{D_k}(x) \end{array}
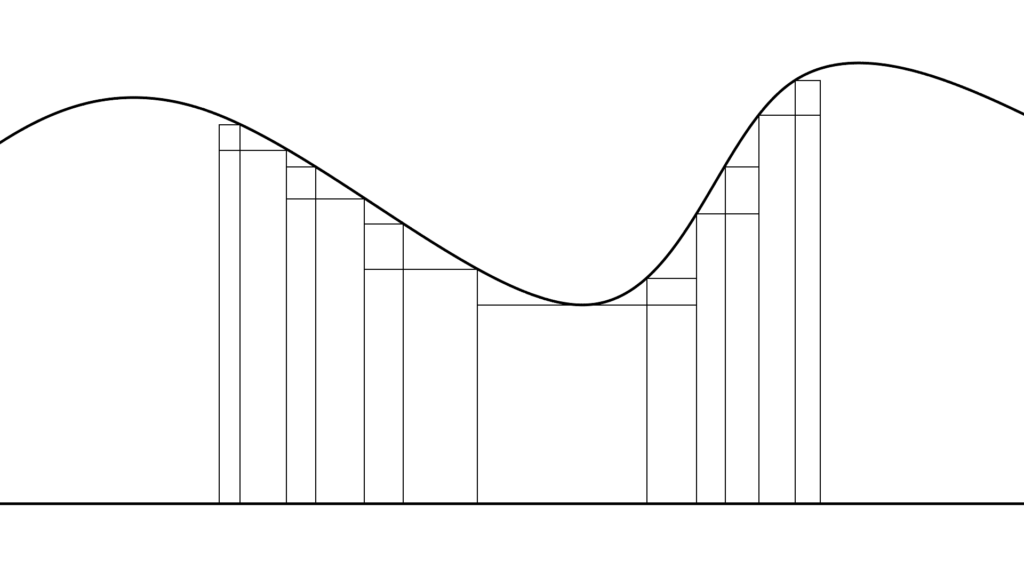
\begin{array}{ccc} D&=&\displaystyle \bigcup_{k=1}^{n} D_k \\ \\ \displaystyle \sum_{k=1}^{n}φ_n(x)μ(dx)&=&\displaystyle \sum_{k=1}^{n}a_k1_{D_k}(x) μ(D_k) \\ \\ \\ μ(dx) &=& μ(D_k) \end{array}
これもまた
\begin{array}{ccl} \displaystyle\int_D f(x) \,dx &=&\displaystyle\lim_{n\to\infty} \left\{ \int_{D}φ_n(x)μ(dx) \right\} \\ \\ \displaystyle\int_D f(x) \,dx &=&\displaystyle\lim_{n\to\infty} \left\{ \sum_{k=1}^{n}a_k1_{D_k}(x) μ(D_k) \right\} \end{array}
「測度である」ことが分かると思います。
(これの詳細はルベーグ積分の記事を参照)
また「積分」が「測度」である以上
\begin{array}{ccc} \displaystyle \int\int_{I_X\times I_Y} f(x,y) \, dxdy \end{array}
「多重積分」なんかも「測度」だと言えます。
ルベーグ積分と微小変化
「リーマン積分」的な感じで分かりやすいように
\begin{array}{ccc} \displaystyle\int_D f(x) \,dx &=&\displaystyle\lim_{n\to\infty} \left\{ \sum_{k=1}^{n}a_k1_{D_k}(x) μ(D_k) \right\} \end{array}
↑ ではこのように表記していますが
\begin{array}{ccr} x&\in&Q \\ \\ x&\in&R\setminus Q \end{array}
「有理数」「無理数」のような
「離散」的なデータを扱う場合
「連続」ではない以上
「微小変化 dx 」をうまく定義できない
\begin{array}{ccc} dx&=&\displaystyle\lim_{h\to 0}(x+h)-x \end{array}
そういう可能性があるので
\begin{array}{lcc} \displaystyle\int_D f(x) \,dμ &=&\displaystyle\lim_{n\to\infty} \left\{ \sum_{k=1}^{n}a_k1_{D_k}(x) μ(D_k) \right\} \\ \\ \displaystyle\int_D f(x) \,dμ(x) &=&\displaystyle\lim_{n\to\infty} \left\{ \sum_{k=1}^{n}a_k1_{D_k}(x) μ(D_k) \right\} \end{array}
より正確に「ルベーグ積分」を記述するために
\begin{array}{ccc} μ(dx)&→& dμ \end{array}
「 D の分割である底辺 dx 」の「測度」については
このように書かれることがあります。
直積測度と多重積分
「積分」を「直積」で考える時
\begin{array}{llllll} X\times Y &=&\{ (x,y) \mid x∈X ∧ y∈Y \} \end{array}
\begin{array}{lcl} D_X &=& \{ x\in X \mid (x,y)∈X\times Y \} \\ \\ D_Y &=& \{ y\in Y \mid (x,y)∈X\times Y \} \end{array}
「直積集合」をこのように定めると
\begin{array}{ccc} μ_X \times μ_Y (D)&=&μ_X(D_X) μ_Y (D_Y) \end{array}
\begin{array}{ccl} μ_X(D_X)&=&\displaystyle \int_{X} 1_{D_X}(x) \, dμ_X(x) \\ \\ &=&\displaystyle \int_{D_X} 1 \, dμ_X(x) \end{array}
\begin{array}{llllll} μ_X \times μ_Y (D)&=& \displaystyle \int_{D_Y} μ_X(D_X) \, dμ_Y(y) \\ \\ μ_X \times μ_Y (D)&=& \displaystyle \int_{D_X} μ_Y(D_Y) \, dμ_X(x) \end{array}
「多重積分」は
このような形になると考えられて
\begin{array}{ccc} \displaystyle \int\int_{I_X\times I_Y} f(x,y) \, dxdy &=&\displaystyle \int_{I_Y} \left( \int_{I_X} f(x,y) \, dx \right) dy \\ \\ \displaystyle \int\int_{I_X\times I_Y} f(x,y) \, dxdy &=&\displaystyle \int_{I_X} \left( \int_{I_Y} f(x,y) \, dy \right) dx \end{array}
ここから
可測長方形の面積
「可測長方形 A 」の「面積 |A| 」は
\begin{array}{ccc} I_X \times I_Y & ⊂ & X\times Y \end{array}
\begin{array}{ccc} A & = & I_X \times I_Y \\ \\ |A| & = & μ_X(I_X)μ_Y(I_Y) \end{array}
「直積測度」の定義を見てわかる通り
こんな感じに定義出来て
\begin{array}{ccc} |∅|&=&0 \end{array}
\begin{array}{ccc} \begin{array}{ccc} i≠j \\ ↓ \\ A_i∩A_j=∅ \end{array} &→& \displaystyle |A|=\sum_{n=1}^{\infty}|A_n| \end{array}
直感的に分かる通り
これは「測度」の要件を満たします。
(定義段階だとこれはまだ分からない)
空集合
「可測長方形」の定義より
\begin{array}{ccc} |A| & = & μ_X(I_X)μ_Y(I_Y) \end{array}
「面積(直積測度)」の定義には
「区間の長さ μ 」が使われてるので
\begin{array}{ccccc} X\times ∅ &=&\{ (x,y) \mid x∈X ∧ y∈∅ \} \\ \\ &=&∅ \\ \\ \\ ∅\times Y &=&\{ (x,y) \mid x∈∅ ∧ y∈Y \} \\ \\ &=&∅ \end{array}
「直積集合の空集合」はこうなることから
\begin{array}{ccc} |∅| & = &0 \end{array}
この結論はすぐに導かれます。
完全加法性
問題はこっち
これを示すのはちょっと大変で
\begin{array}{ccc} \begin{array}{ccc} i≠j \\ ↓ \\ A_i∩A_j=∅ \end{array} &→& \displaystyle |A|=\sum_{n=1}^{\infty}|A_n| \end{array}
この結論を得るためには
\begin{array}{lcc} A&⊂&X\times Y \\ \\ A_n&⊂&X\times Y \end{array}
\begin{array}{ccc} A&=&\displaystyle\bigcup_{n=1}^{\infty}A_n \end{array}
まず前提を満たすために
「非交和な集合 A_n 」を考える必要があって
(これを作る方法は拡張定理の話で出てくる)
その上で
\begin{array}{ccc} \displaystyle |A|&=&\displaystyle\sum_{n=1}^{\infty}|A_n| \end{array}
こうなることを示す必要があります。
直積測度の定義から考える
というわけで
\begin{array}{ccc} \displaystyle |A|&=&\displaystyle\sum_{n=1}^{\infty}|A_n| \end{array}
これを示すために
\begin{array}{ccc} A&=& I_X\times I_Y \\ \\ |A|&=&μ_X(I_X)μ_Y(I_Y) \end{array}
とりあえず「直積測度」の定義を考えてみると
\begin{array}{ccc} |A|&→&|A_n| \end{array}
この式から
どうにかして A_n に繋げる必要がある
そんな漠然とした方針が定まるので
\begin{array}{ccc} μ(I)&→&μ(I_n) \end{array}
この式をどうにか良い感じに分解できないか、とか
そんな疑問を解決していく形で話を進めていきます。
測度の積
そもそもの話
\begin{array}{ccc} μ(I)&→&μ(I_n) \end{array}
この μ は「区間の長さ(前測度)」ですから
\begin{array}{ccc} μ(I)&=&\displaystyle\sum_{n=1}^{\infty}μ(I_n) \end{array}
「完全加法性」を満たします。
(本題から逸れるので詳細は別記事)
ということは
「非交和」を仮定すると
「測度の積(直積測度)」は以下のようになり
\begin{array}{ccc} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle\sum_{n=1}^{\infty}μ(I_{Xn})\sum_{m=1}^{\infty}μ(I_{Ym}) \end{array}
総和の性質を考えると
\begin{array}{ccc} (a_1+a_2)(b_1+b_2)&=&\begin{array}{lcc} a_1(b_1+b_2) \\ \\ a_2(b_1+b_2) \end{array} \end{array}
\begin{array}{ccc} \displaystyle\sum_{i=1}^{n}a_i \sum_{j=1}^{m} b_j &=& \displaystyle\sum_{i=1}^{n} \sum_{j=1}^{m} a_ib_j \end{array}
前提より
「総和」は「区間の長さ」であるため
「収束する」のは明らかであることから
\begin{array}{ccc} \displaystyle\sum_{n=1}^{\infty}a_n \sum_{m=1}^{\infty} b_m &=& \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} a_nb_m \end{array}
結果的に
これは ↓ のように書き換えることができます。
\begin{array}{ccl} μ_X\times μ_Y(I_{X}\times I_{Y}) &=& μ_X(I_X)μ_Y(I_Y) \\ \\ &=&\displaystyle\sum_{n=1}^{\infty}μ(I_{Xn})\sum_{m=1}^{\infty}μ(I_{Ym}) \\ \\ &=& \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{\infty}μ(I_{Xn})μ(I_{Ym})\end{array}
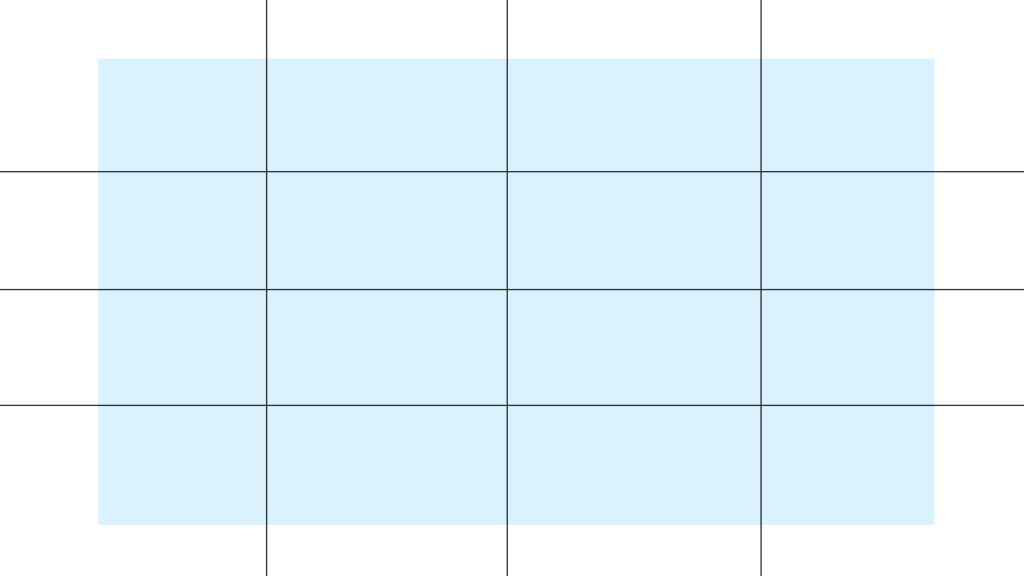
ちょっと複雑ですが
イメージはマス目です。
\begin{array}{ccc} A_{nm}&=& I_{Xn} \times I_{Ym} \\ \\ 長方形 && 区間 \times 区間 \end{array}
これが「長方形」だと実感できれば
わりとすんなり理解できると思います。
完全加法性っぽけど
以上より
\begin{array}{ccc} μ_X(I_X)μ_Y(I_Y) &=& \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} μ(I_{Xn})μ(I_{Ym}) \end{array}
直感的には
「完全加法性っぽい」ものが求められたわけですが
\begin{array}{ccc} \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} μ(I_{Xn})μ(I_{Ym}) \end{array}
「二重に無限が使われてる」点で
これはなんかちょっと怪しく見えます。
なのでその怪しさを解消するために
\begin{array}{ccc} \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} &&→&& \displaystyle\sum_{n_*=1}^{\infty} \end{array}
どうにかこの二重の状態を解消したいです。
シンプルなようで複雑な話
「二重級数」の問題に対しては
実は「コーシー積」という解答があるんですが
\begin{array}{ccc} \displaystyle\sum_{n=1}^{\infty} μ(I_{Xn}) &=&\displaystyle μ(I_{X}) \\ \\ \displaystyle \sum_{m=1}^{\infty}μ(I_{Ym})&=& \displaystyle μ(I_{Y}) \end{array}
これはちょっと複雑なので
この記事ではざっと解説します。
というわけで
ここでは結論だけ書いておくと
まず「区間の長さ」が「収束する」のは定義
そして「測度が正の値である」ことも定義ですから
「コーシー積」に必要な前提は満たされているので
\begin{array}{ccc} \displaystyle\sum_{n=1}^{\infty}μ(I_{X_n}) \sum_{m=1}^{\infty} μ(I_{Y_m}) &=& \displaystyle\sum_{n=1}^{\infty} \sum_{m=1}^{n} μ(I_{X_m})μ(I_{Y_{n-m+1}}) \end{array}
その結果として
このような形で無限を1つにまとめることができる。
(縦横じゃなく斜めで番号付けする感じ)
そして ↑ の結果から
\begin{array}{ccccccc} n & m & n-m+1 &&→&&n_* \\ \\ 1 & 1 & 1 &&→&& 1 \\ \\ 2 & 1 & 2 &&→&& 2 \\ \\ 2 & 2 & 1 &&→&& 3 \\ \\ 3& 1 &3 &&→&& 4 \\ \\ 3& 2&2 &&→&& 5 \\ \\ & & &&\vdots \end{array}
「添え字」の対応付けを変更する形で
改めてこのような添え字 n_* を定義すると
\begin{array}{ccc} μ_X(I_X)μ_Y(I_Y) &=& \displaystyle\sum_{n_*=1}^{\infty} μ(I_{X_{n_*}})μ(I_{Y_{n_*}}) \end{array}
「完全加法性」を意味する
怪しくないこの形を得ることができます。
(規則的に分割している場合に限定された話)
いろんな分割に対応したい
↑ の話によって
「一部で完全加法性が成立する」のは分かりました。
\begin{array}{ccc} μ_X(I_X)μ_Y(I_Y) &=& \displaystyle\sum_{n_*=1}^{\infty} μ(I_{X_{n_*}})μ(I_{Y_{n_*}}) \end{array}

具体的には
このような無限分割ならいけるんですが
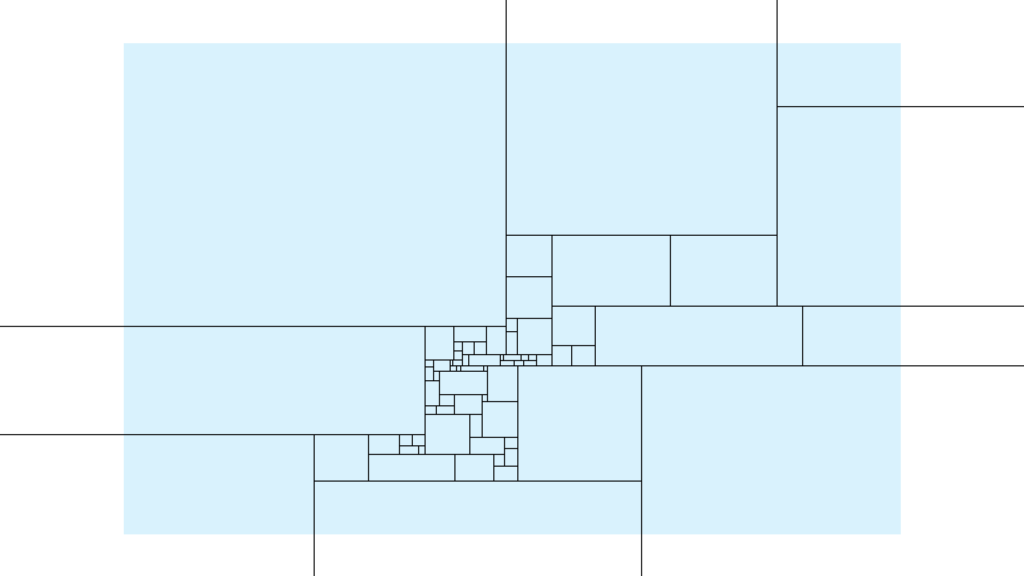
分割の方法自体は無数に考えられるので
↑ だけでは全てのパターンをカバーできていません。
図形と定義関数
↑ の問題を解消するために
\begin{array}{ccc} 1_D(x) &=&\displaystyle \left\{ \begin{array}{ccl} 1 &&x\in D \\ \\ 0 &&x\not\in D \end{array} \right. \\ \\ \displaystyle \int_{X} 1_D(x) \,dx &=&μ(D) \end{array}
分かりやすく
「ルベーグ測度」を参考にするなら
図形を1つずつ確認できる
「定義関数」を使えば
\begin{array}{ccc} 1_{X\times Y} \Bigl( (x,y) \Bigr) &=&\displaystyle \left\{ \begin{array}{ccl} 1 && (x,y) \in X\times Y \\ \\ 0 && (x,y) \not\in X\times Y \end{array} \right. \\ \\ \displaystyle \int_{X\times Y} 1_{X\times Y} \Bigl( (x,y) \Bigr) \,dμ &=& μ(X\times Y) \end{array}
まだこの時点だとなんとなくですが
良い感じに定義できそうな気がします。
定義関数と測度
I が「区間」であるとして
\begin{array}{lcl} [x]_a^b &=&\displaystyle\int_I 1 \,dμ(x) \\ \\ μ(I)&=&\displaystyle\int_{X}1_I(x) \,dμ(x) \\ \\ μ(I_n)&=&\displaystyle\int_{X}1_{I_n}(x) \,dμ(x) \end{array}
「積分」すると「長さ」になる
こんな感じの「定義関数」を考えると
( I は可測集合まで拡張できる)
「定義関数」は
「 0 か 1 を返す関数」ですから
\begin{array}{ccc} \begin{array}{ccc} x\in I_X \\ \\ y\in I_Y \end{array} &→& (x,y)\in I_X\times I_Y \end{array}
「直積集合 I_X\times I_Y の要素 (x,y) 」と
「集合 I_X , I_Y の要素 x,y 」を繋げる形で
\begin{array}{ccc} A&=& I_X\times I_Y \\ \\ 1_{A}\Bigl( (x,y) \Bigr)&=&1_{I_X}(x)1_{I_Y}(y) \end{array}
「直積測度」と同様
このような「定義関数」を定めることができるので
\begin{array}{lcl} 1_{A_1}\Bigl( (x,y) \Bigr)&=&1_{I_{X1}}(x)1_{I_{Y1}}(y) \\ \\ 1_{A_2}\Bigl( (x,y) \Bigr)&=&1_{I_{X2}}(x)1_{I_{Y2}}(y) \\ \\ &\vdots \\ \\ 1_{A_n}\Bigl( (x,y) \Bigr)&=&1_{I_{Xn}}(x)1_{I_{Yn}}(y) \\ \\ &\vdots \end{array}
「可測長方形の分割 A_n 」については
このような形で定義できると言えます。
(分割方法に関係なく)
図形と定義関数の足し算
定義関数による定義を軸に
\begin{array}{ccc} 1_{A_n}\Bigl( (x,y) \Bigr)&=&\displaystyle \left\{ \begin{array}{ccl} 1 &&(x,y)\in A_n \\ \\ 0 &&(x,y)\not\in A_n \end{array} \right. \end{array}
そもそもの着地である「完全加法性」
これを説明する「図形 A_n の足し算」を考えると
\begin{array}{ccc} μ(A_1)+μ(A_2) \end{array}
今度はこれに問題が無いか
きちんと確認したくなります。
具体的には
\begin{array}{ccc} 1_{P}(x)+1_{Q}(x)&=&\displaystyle \left\{ \begin{array}{ccl} 2 && x\in P∧ x\in Q \\ \\ 1 &&x\in P ∧ x\not\in Q \\ \\ 1 &&x\in Q ∧ x\not\in P \\ \\ 0 &&x\not\in P∪Q \end{array} \right. \\ \\ \\ &=&\displaystyle \left\{ \begin{array}{ccl} 1 \,\, \mathrm{or} \,\, 2 &&x\in P ∪ Q \\ \\ 0 &&x\not\in P∪Q \end{array} \right. \end{array}
こうなることを確認したいわけですが
\begin{array}{ccc} x \in P ∨ x\in Q &&⇔&& 1_{P}(x)+1_{Q}(x)≥1 \end{array}
これはほぼ集合の定義なので
これ以上は特に語ることがありません。
(有限個で完全加法性が成立するのは明らか)
ただ
「非交和 \mathrm{disjoint} 」を前提とする場合
\begin{array}{ccl} A&=&\displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ A&=&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \end{array}
「無限個の図形」の足し算が ↓ のようになる
\begin{array}{lcl} 1_{A}\Bigl( (x,y) \Bigr)&=&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
これは明らかではないので
こうなるかどうかきちんと確認する必要があります。
(集合と定義関数の定義が分かれば明らか)
怪しい部分と定義
↑ は直感的には明らかですが
\begin{array}{ccc} 1_{A}\Bigl( (x,y) \Bigr)&=&1_{I_X}(x)1_{I_Y}(y) \end{array}
「無限」が絡む以上
↓ はちょっと怪しいので
\begin{array}{lcl} 1_{A}\Bigl( (x,y) \Bigr)&=&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
これらが成立するかどうかについて
きちんと定義から確認を行っておきます。
集合と定義関数
まず ↓ についてですが
\begin{array}{ccc} 1_{A}\Bigl( (x,y) \Bigr)&=&1_{I_X}(x)1_{I_Y}(y) \end{array}
これは「定義関数」と
\begin{array}{ccc} 1_D(x) &=&\displaystyle \left\{ \begin{array}{ccl} 1 &&x\in D \\ \\ 0 &&x\not\in D \end{array} \right. \end{array}
「直積集合」の定義から
\begin{array}{ccc} (x,y)\in A &⇔& x\in I_X ∧ y\in I_Y \end{array}
特に難しいことをするでもなく
(ここでは非交和を前提とします)
\begin{array}{ccc} (x,y)\in A &⇔& 1_{A}\Bigl( (x,y) \Bigr)=1 \\ \\ x\in I_X ∧ y\in I_Y&⇔& \Bigl( 1_{I_X}(x)=1 \Bigr) ∧ \Bigl( 1_{I_Y}(y)=1 \Bigr) \\ \\ \\ (x,y) \not\in A &⇔& 1_{A}\Bigl( (x,y) \Bigr)=0 \\ \\ x\not\in I_X ∨ y\not\in I_Y &⇔& \Bigl( 1_{I_X}(x)=0 \Bigr) ∨ \Bigl( 1_{I_Y}(y)=0 \Bigr) \end{array}
そのまま正しくなることを確認できます。
(四則演算の積と論理積の関係)
定義関数と無限和
↓ については
\begin{array}{lcl} 1_{A}\Bigl( (x,y) \Bigr)&=&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
ちょっと大変ですが
\begin{array}{lcc} i≠j→ A_i∩A_j=∅ &&⇒&& A=\displaystyle\bigcup_{n=1}^{\infty} A_n \end{array}
\begin{array}{ccc} A_n&=&I_{X_n} \times I_{Y_n} \\ \\ (x,y) \in A_n &⇔& x\in I_{X_n} ∧ y\in I_{Y_n} \\ \\ \end{array}
「完全加法性」を考えるために
これを前提とすると
\begin{array}{lclcc} (x,y)\in A &⇔&(x,y)\in \displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ &⇔&\exists n\in N \,\, (x,y)\in A_n \\ \\ &⇔&\exists n\in N \,\, (x,y)\in I_{X_n} \times I_{Y_n} \\ \\ &⇔&\exists n\in N \,\, x\in I_{X_n}∧y\in I_{Y_n} \end{array}
この論理式が得られるので
後は「定義関数」の定義を考えれば
\begin{array}{ccc} (x,y)\in A &⇔&1_{A}\Bigl( (x,y) \Bigr)=1 \\ \\ \exists n\in N \,\, (x,y)\in A_n &⇔& \displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr)=1 \end{array}
こっちはこのようになり
( A_n が互いに素でないなら総和は 1 以上)
\begin{array}{ccc} x\in I_X∧y\in I_Y &⇔& 1_{I_X}(x)1_{I_Y}(y)=1 \\ \\ \exists n\in N \,\, x\in I_{X_n}∧y\in I_{Y_n}&⇔&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y)=1 \end{array}
こっちはこんな感じになります。
(こっちも互いに素でないなら総和は 1 以上)
互いに素な無限分割は本当にできるのか
念のため確認しておくと
\begin{array}{ccl} A&=&\displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ I_{X}\times I_{Y}&=&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \end{array}
これは「可測長方形」の話
つまり「区間」同士の「直積集合」の話なので
\begin{array}{ccc} i≠j &→& I_i∩I_j=∅ \end{array}
\begin{array}{ccc} I&=&\displaystyle\bigcup_{n=1}^{\infty} I_n \end{array}
「区間」はこのように無限分割できることから
(これの詳細は基本集合の記事で語っています)
\begin{array}{ccc} x \in I_{X} &⇔& \exists n\in N \,\, x \in I_{X_n} \\ \\ y \in I_{Y} &⇔& \exists n\in N \,\, y \in I_{Y_n} \end{array}

マス目をイメージの基盤として
「直積集合(可測長方形)」を考えると
「可測長方形」は ↓ のようになるので
\begin{array}{ccc} (x,y) \in I_{X}\times I_{Y} &⇔& \displaystyle (x,y) \in \bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \\ \\ &⇔& \exists n \in N \,\, (x,y) \in I_{Xn}\times I_{Yn} \\ \\ &⇔& \exists n \in N \,\, x \in I_{Xn} ∧ y \in I_{Yn} \end{array}
「可測長方形」もまた
「互いに素」な集合に無限分割できると言えます。
(直積集合と区間と無限和集合の定義の確認)
定義関数を使って式変形してみる
以上の結果を使って
着地を目指してみると
\begin{array}{ccc} |A|&=&μ_X(I_X)μ_Y(I_Y) \end{array}
この式は
\begin{array}{lcl} μ_X(I_{X})&=&\displaystyle\int_{X}1_{I_{X}}(x) \,dμ(x) \\ \\ μ_Y(I_{Y})&=&\displaystyle\int_{Y}1_{I_{Y}}(y) \,dμ(y) \end{array}
「測度」が変形できることから
\begin{array}{ccl} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle\left( \int_X 1_{I_X}(x) \,dμ(x) \right) μ_Y(I_Y) \end{array}
このように変形出来て
\begin{array}{ccc}\displaystyle a\int f(x)\,dx&=&\displaystyle\int af(x)\,dx \end{array}
積分の基本的な性質を考えると
\begin{array}{ccl} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle\left( \int_X 1_{I_X}(x) \,dμ(x) \right) μ_Y(I_Y) \\ \\ &=&\displaystyle \int_X μ_Y(I_Y)1_{I_X}(x) \,dμ(x) \end{array}
更にこのように変形でき
( μ_X は I_Y の影響を受けない)
「定義関数」の性質を利用して
同様の変形を行うと
\begin{array}{ccl} μ_Y(I_Y)1_{I_X}(x)&=&\displaystyle 1_{I_X}(x)\left( \int_Y 1_{I_Y}(y) \,dμ(y) \right) \\ \\ &=&\displaystyle \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y) \end{array}
この部分もまたこのように変形できます。
定義関数から測度へ
以上の変形により
\begin{array}{ccc} A&=& I_X\times I_Y \\ \\ 1_{A}\Bigl( (x,y) \Bigr)&=&1_{I_X}(x)1_{I_Y}(y) \end{array}
\begin{array}{ccc} 1_{P}(x)+1_{Q}(x) &=&\displaystyle \left\{ \begin{array}{ccl} 1 &&x\in P ∪ Q \\ \\ 0 &&x\not\in P∪Q \end{array} \right. \end{array}
定義関数を式に入れることができたので
\begin{array}{ccl} 1_{A}\Bigl( (x,y) \Bigr)&=&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
これらの関係が使えるようになるため
(非交和でないなら右が大きくなる)
後は「積分の和」を考えれば
\begin{array}{ccc}\displaystyle \int \Bigl( f(x)+g(x) \Bigr) \, dx &=&\displaystyle \int f(x) \, dx+\displaystyle \int g(x) \, dx \\ \\ \displaystyle\int \left(\sum_{n=1}^{k}f_n(x) \right) \,dx&=&\displaystyle \sum_{n=1}^{k} \int f_n(x) \,dx \end{array}
さらに ↑ の式を変形する形で
\begin{array}{ccl}\displaystyle \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y)&=&\displaystyle \int_Y \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \,dμ(y)\\ \\ &=&\displaystyle \sum_{n=1}^{\infty} \int_Y 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \,dμ(y) \\ \\ &=&\displaystyle \sum_{n=1}^{\infty} \left( 1_{I_{Xn}}(x) \int_Y 1_{I_{Yn}}(y) \,dμ(y) \right) \\ \\ &=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \end{array}
このような式が得られます。
求めたい形
そしてここまで来れば
\begin{array}{ccl} μ_Y(I_Y)1_{I_X}(x)&=&\displaystyle 1_{I_X}(x)\left( \int_Y 1_{I_Y}(y) \,dμ(y) \right) \\ \\ &=&\displaystyle \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y) \\ \\ &=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \end{array}
このようになることから
\begin{array}{ccl} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle\left( \int_X 1_{I_X}(x) \,dμ(x) \right) μ_Y(I_Y) \\ \\ &=&\displaystyle \int_X μ_Y(I_Y)1_{I_X}(x) \,dμ(x) \\ \\ \\ &=&\displaystyle \int_X \left( \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y) \right) \,dμ(x) \\ \\ &=&\displaystyle \int_X \left( \sum_{n=1}^{\infty} 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \right) \,dμ(x)\end{array}
これはこうなるので
\begin{array}{ccl} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle \int_X \left( \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y) \right) \,dμ(x) \\ \\ &=&\displaystyle \int_X \left( \sum_{n=1}^{\infty} 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \right) \,dμ(x) \\ \\ \\ &=&\displaystyle \sum_{n=1}^{\infty}\left(\int_X 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \,dμ(x) \right) \\ \\ &=&\displaystyle \sum_{n=1}^{\infty}\left(μ_Y (I_{Yn}) \int_X 1_{I_{Xn}}(x) \,dμ(x) \right) \\ \\ \\ &=&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \end{array}
結果、この形が得られます。
まとめ
整理すると
\begin{array}{ccl} 1_{A}\Bigl( (x,y) \Bigr)&=&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&=&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
この「定義関数」の関係から
\begin{array}{ccl} |A|&=&\displaystyle\sum_{n=1}^{\infty}|I_{Xn}\times I_{Yn}| \\ \\ μ_X(I_X)μ_Y(I_Y)&=&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \end{array}
この結論が得られました。
(これにより任意の図形 A_n に分割できると言える)
劣加法性
「非交和 \mathrm{disjoint} 」を条件に入れない
\begin{array}{ccl} A&⊂&\displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ I_X \times I_Y&⊂&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \end{array}
「完全加法性」の一般化として
\begin{array}{ccl} |A|&≤&\displaystyle\sum_{n=1}^{\infty}|I_{Xn}\times I_{Yn}| \\ \\ μ_X(I_X)μ_Y(I_Y)&≤&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \end{array}
この「劣加法性」は
「完全加法性」と同様の流れで証明できます。
劣加法性と定義関数
「互いに素 \mathrm{disjoint} 」を仮定しない場合
\begin{array}{ccc} A&=& I_X\times I_Y \\ \\ 1_{A}\Bigl( (x,y) \Bigr)&=&1_{I_X}(x)1_{I_Y}(y) \end{array}
「定義関数」の性質と
\begin{array}{ccc} 1_{P}(x)+1_{Q}(x) &=&\displaystyle \left\{ \begin{array}{ccl} 1 \,\, \mathrm{or} \,\, 2 &&x\in P ∪ Q \\ \\ 0 &&x\not\in P∪Q \end{array} \right. \end{array}
定義された集合の関係を考慮すると
\begin{array}{ccl} A&⊂&\displaystyle\bigcup_{n=1}^{\infty} A_n \\ \\ I_X \times I_Y&⊂&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \end{array}
以下の関係は
\begin{array}{ccl} 1_{A}\Bigl( (x,y) \Bigr)&≤&\displaystyle \sum_{n=1}^{\infty} 1_{A_n}\Bigl( (x,y) \Bigr) \\ \\ 1_{I_X}(x)1_{I_Y}(y)&≤&\displaystyle \sum_{n=1}^{\infty} 1_{I_{Xn}}(x)1_{I_{Yn}}(y) \end{array}
「 A にはない A_n の点 (x,y) 」や
「 A_i を全部持つ A_j 」などが考えられるので
「同じ = 」ではなくこのようになります。
定義関数と式変形
以上が「完全加法性」との違いで
\begin{array}{ccl} μ_X(I_X)μ_Y(I_Y)&=&\displaystyle \int_X \left( \int_Y 1_{I_X}(x)1_{I_Y}(y) \,dμ(y) \right) \,dμ(x) \\ \\ μ_X(I_X)μ_Y(I_Y)&\textcolor{pink}{≤}&\displaystyle \int_X \left( \int_Y \left(\sum_{n=1}^{\infty} 1_{I_{Xn}}(x) 1_{Yn}(y) \right) \,dμ(y) \right) \,dμ(x) \end{array}
「分割」の段階で大小関係は変化しますが
「定義関数」の等式はそのまま
\begin{array}{ccl}&& \displaystyle \int_X \left( \int_Y \left(\sum_{n=1}^{\infty} 1_{I_{Xn}}(x) 1_{Yn}(y) \right) \,dμ(y) \right) \,dμ(x) \\ \\ &=& \displaystyle \int_X \left( \sum_{n=1}^{\infty} 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \right) \,dμ(x) \\ \\ \\ &=&\displaystyle \sum_{n=1}^{\infty}\left(\int_X 1_{I_{Xn}}(x) μ_Y (I_{Yn}) \,dμ(x) \right) \\ \\ &=&\displaystyle \sum_{n=1}^{\infty}\left(μ_Y (I_{Yn}) \int_X 1_{I_{Xn}}(x) \,dμ(x) \right) \\ \\ \\ &=&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \end{array}
同様の流れで
式変形はこのようになり
結果として
\begin{array}{ccl} I_X \times I_Y&⊂&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \\ \\ μ_X(I_X)μ_Y(I_Y)&≤&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \\ \\ |A|&≤&\displaystyle\sum_{n=1}^{\infty}|I_{Xn}\times I_{Yn}| \end{array}
この関係が導かれます。
直積集合の外測度
以上の話から
\begin{array}{ccc} |I_X\times I_Y|&=& μ_X(I_X)μ_Y(I_Y) \end{array}
この「可測長方形の面積(直積測度)」は
「前測度・測度である」と言えるので
\begin{array}{ccc} A &⊂&\displaystyle \bigcup_{i=1}^{\infty} A_n \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
「ルベーグ外測度」と同様の流れで
\begin{array}{ccl} μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \,\, \middle| \,\, A ⊂ \bigcup_{i=1}^{\infty} A_n \right\} \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} μ(A_n) \,\, \middle| \,\, A ⊂ \bigcup_{i=1}^{\infty} A_n \right\} \end{array}
「直積空間」における「外測度」として
このような「外測度」を考えることができます。
外測度上可測な直積集合は完全加法族
これは「直積集合の面積 |\cdot | 」が
「測度である」と分かっていることから
\begin{array}{ccl} |A|&=&\displaystyle\sum_{n=1}^{\infty}|I_{Xn}\times I_{Yn}| \\ \\ μ_X(I_X)μ_Y(I_Y)&=&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \end{array}
「カラテオドリの基本定理」より
「外測度」と同様の理屈で示すことができて
\begin{array}{rcr} && ∅ \in L_{μ_{X\times Y}} \\ \\ A \in L_{μ_{X\times Y}}&→& A^c \in L_{μ_{X\times Y}} \\ \\ A_1,A_2,A_3,... \in L_{μ_{X\times Y}} &→& \displaystyle\bigcup_{n=1}^{\infty} A_n \in L_{μ_{X\times Y}} \end{array}
結果として
「外測度 μ_{X\times Y} 」上で「可測な集合全体 L_{μ_{X\times Y}} 」は
\begin{array}{ccc} μ_{X\times Y}(S)&≥&μ_{X\times Y}(S∩A)+μ_{X\times Y}(S∩A^c) \end{array}
「完全加法族」になります。
(長くなるので詳細は別の記事で)
直積測度空間と測度空間
結論を先に言っておくと
\begin{array}{ccccc} \begin{array}{l} (X,σ_X,μ_X) \\ \\ (X,σ_Y,μ_Y) \end{array} &&→&&\displaystyle \Bigl( X\times Y, σ_X \otimes σ_Y, μ_X \times μ_Y \Bigr) \end{array}
「測度空間」の「直積」で得られた
「直積測度空間 \Bigl( X\times Y, σ_X \otimes σ_Y, μ_X \times μ_Y \Bigr) 」は
「測度空間 (U,σ_U,μ) 」になります。
これは「可測長方形の面積 |\cdot | 」が
「測度である」と分かっていれば
\begin{array}{ccc} I_X \times I_Y&⊂&\displaystyle\bigcup_{n=1}^{\infty} I_{Xn}\times I_{Yn} \\ \\ μ_X(I_X)μ_Y(I_Y)&≤&\displaystyle \sum_{n=1}^{\infty} μ_X (I_{Xn})μ_Y (I_{Yn}) \\ \\ |A|&≤&\displaystyle\sum_{n=1}^{\infty}|I_{Xn}\times I_{Yn}| \end{array}
直感的には明らかなので
特に疑問の余地はありません。
しかし
「直積集合の外測度 μ_{X\times Y} 」を考えた時
\begin{array}{ccc} A &⊂&\displaystyle \bigcup_{i=1}^{\infty} A_n \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
まだ自明であるとは言えないので
ちゃんと「測度になるのか」
厳密に確認する必要があります。
直積集合の外測度とホップの拡張定理
これは簡単には
\begin{array}{ccc} A &⊂&\displaystyle \bigcup_{n=1}^{\infty} A_n \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
「直積集合の外測度 μ_{X\times Y} 」を
「測度 |\cdot | 」の「拡張」と見做せば
\begin{array}{ccc} X\times Y & σ_X \otimes σ_Y & |\cdot | \\ \\ & ↓ & ↓ \\ \\ X\times Y & σ_X \otimes σ_Y & μ_{X\times Y} \end{array}
「ホップの拡張定理」が使えるので
この定理を飲み込めるなら
\begin{array}{ccc} \forall A \in σ_X \otimes σ_Y & |A|=μ_{X\times Y}(A) \end{array}
「測度 |\cdot | の拡張 μ_{X\times Y} 」として
その「存在」「一意性」は直ちに証明されます。
直積集合の測度と外測度
↑ の結果は更に抽象化できて
\begin{array}{ccc} A &⊂&\displaystyle \bigcup_{i=1}^{\infty} A_n \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
記号はそのまま
「可測長方形の面積 |\cdot | 」の存在から
\begin{array}{ccc} |A|&=&μ_X(I_X)μ_Y(I_Y) \end{array}
「拡張定理」の手順に倣い
\begin{array}{ccc} |∅| &=& 0 \end{array}
\begin{array}{ccc} \mathrm{disjoint} &→& |A|=\displaystyle\sum_{n=1}^{\infty}|A_n| \end{array}
以上の性質を満たす
「直積集合の測度」として記号を再定義すると
(長方形の面積や要素の個数などを一般化した測度)
\begin{array}{ccc} \forall A\in σ_X\otimes σ_Y & |A|=μ_{X\times Y}(A) \end{array}
また「ホップの拡張定理」が適用できるので
\begin{array}{ccc} μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
この「存在」と「一意性」もまた導かれます。
外測度であることの確認
ただこれだけ書かれてもって感じだと思うので
この「直積測度 μ_{X\times Y} 」が
\begin{array}{ccc} μ_{X\times Y}(∅)=0 \\ \\ 0≤μ_{X\times Y}(A)≤\infty \end{array}
\begin{array}{ccc} A⊂B &&→&& μ_{X\times Y}(A)≤μ_{X\times Y}(B) \end{array}
\begin{array}{llllll} \displaystyle μ_{X\times Y}\left( \bigcup_{n=1}^{\infty} A_n \right) &≤&\displaystyle \sum_{n=1}^{\infty}μ_{X\times Y}(A_n) \end{array}
以上の性質を持つ
「外測度である」か
念のため軽く示してみます。
空集合
これについては
\begin{array}{ccc} X\times ∅ &=&\{ (x,y) \mid x∈X ∧ y∈∅ \} &=&∅ \\ \\ ∅\times Y &=&\{ (x,y) \mid x∈∅ ∧ y∈Y \} &=&∅ \end{array}
「直積集合」の定義より
\begin{array}{ccc} \displaystyle X \times ∅&=& ∅ \times Y \\ \\ &=& ∅ \end{array}
「空集合の直積」が
必ず「空集合」になることから
以下の等式が成立すると言えるので
\begin{array}{ccc} |X \times ∅|&=&μ_X(X) μ_Y(∅) \\ \\ |∅ \times Y| &=&μ_X(∅) μ_Y(Y) \end{array}
「測度空間 (X,σ_X,μ_X) \,\, (Y,σ_Y,μ_Y) の定義」と
「直積測度」の定義から
\begin{array}{ccc} μ_{X\times Y}(∅) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |∅| \right\} \end{array}
「直積測度の外測度」の最小値が 0 であるため
\begin{array}{llllll} \displaystyle μ_{X\times Y}(∅)&=&0 \end{array}
この値は 0 になると言えます。
定義域と終域
これについては直感的に分かる通り
\begin{array}{ccccc} \begin{array}{ccccc} 0≤ μ_X(A) ≤\infty \\ \\ 0≤ μ_Y(B) ≤\infty \end{array} &&→&&0≤ |A\times B| ≤\infty \end{array}
↓
\begin{array}{ccccc} 0&≤& μ_{X\times Y}(A\times B) &≤&\infty \end{array}
特に語ることはありません。
単調性
これもそのままで
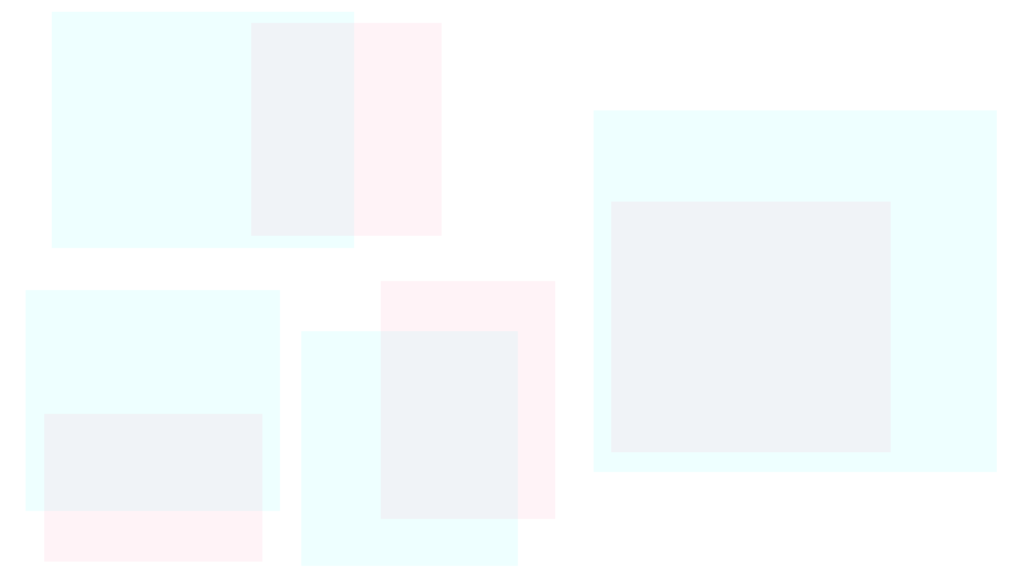
\begin{array}{llllll} A_X\times A_Y ⊂ B_X\times B_Y &&→&& \begin{array}{c} A_X⊂B_X \\ \\ A_Y⊂B_Y \end{array} \end{array}
これは「直積集合」の定義より
必ずこうなることから
\begin{array}{ccccc} \begin{array}{c} A_X⊂B_X \\ \\ A_Y⊂B_Y \end{array} &&→&& A_X\times A_Y ⊂ B_X\times B_Y \\ \\ \\ \begin{array}{c} μ_X(A_X)≤μ_X(B_X) \\ \\ μ_Y(A_Y)≤μ_Y(B_Y) \end{array} &&→&& μ_X(A_X)μ_Y( A_Y) ≤ μ_X(B_X) μ_Y(B_Y) \end{array}
「測度」の「単調性」を考えれば
\begin{array}{ccc} \begin{array}{ccc} |A|≤μ_{X\times Y}(A) ≤ |A| \\ \\ |B| ≤ μ_{X\times Y}(B) ≤ |B| \end{array} &&→&& μ_{X\times Y}(A)≤μ_{X\times Y}(B) \end{array}
特に何を考えるまでもなくこうなります。
(上下から抑えることが可能)
劣加法性
これについては
\begin{array}{ccc} A &⊂&\displaystyle \bigcup_{i=1}^{\infty} A_n \\ \\ μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
「直積集合の測度 | \cdot | 」の性質から
\begin{array}{ccr} μ_{X\times Y}(A) &=& \displaystyle \inf\left\{ \sum_{n=1}^{\infty} |A_n| \right\} \\ \\ μ_{X\times Y}(A) &≤& \displaystyle \left\{ \sum_{n=1}^{\infty} |A_n| \right\} \end{array}
「下限」の存在より
以下のような ε>0 の存在が考えられるので
\begin{array}{ccc} \displaystyle \sum_{n=1}^{\infty} |A_n| &<&μ_{X\times Y}(A)+ε \end{array}
そのまま「拡張定理」の手順をなぞるだけで
\begin{array}{rcr} \displaystyle A_m&⊂&\displaystyle\bigcup_{n=1}^{\infty}I_{mn} \\ \\ \displaystyle \bigcup_{m=1}^{\infty}A_m&⊂&\displaystyle \bigcup_{m=1}^{\infty}\bigcup_{n=1}^{\infty}I_{mn} \end{array}
\begin{array}{llllll} \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}A_m \right) &≤&\displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}\bigcup_{n=1}^{\infty}I_{mn} \right) \end{array}
\begin{array}{rcr} \displaystyle μ_{X\times Y} \left( \bigcup_{n=1}^{\infty}I_{mn} \right)&≤&\displaystyle \sum_{n=1}^{\infty}|I_{mn}| \\ \\ \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}\bigcup_{n=1}^{\infty}I_{mn} \right)&≤&\displaystyle \sum_{m=1}^{\infty}\sum_{n=1}^{\infty}|I_{mn}| \end{array}
\begin{array}{rcr} \displaystyle \sum_{n=1}^{\infty} |I_{mn}|&<& μ_{X\times Y}(A_m) + ε \\ \\ \displaystyle \sum_{m=1}^{\infty}\sum_{n=1}^{\infty} |I_{mn}|&<&\displaystyle \sum_{m=1}^{\infty}\Bigl( μ_{X\times Y}(A_m) + ε \Bigr) \end{array}
ちょっと複雑ですが
\begin{array}{lclcc} \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}A_m \right) &≤&\displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}\bigcup_{n=1}^{\infty}I_{mn} \right) \\ \\ &&\displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}\bigcup_{n=1}^{\infty}I_{mn} \right)&≤&\displaystyle \sum_{m=1}^{\infty}\sum_{n=1}^{\infty} |I_{mn}| \end{array}
\begin{array}{lcl} \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}A_m \right) &<&\displaystyle \sum_{m=1}^{\infty}\Bigl( μ_{X\times Y}(A_m) + ε \Bigr) \\ \\ \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}A_m \right) &<&\displaystyle \sum_{m=1}^{\infty}\Bigl( μ_{X\times Y}(A_m) + \frac{ε}{2^n} \Bigr) \\ \\ \displaystyle μ_{X\times Y} \left( \bigcup_{m=1}^{\infty}A_m \right) &<&\displaystyle \sum_{m=1}^{\infty}\Bigl( μ_{X\times Y}(A_m) \Bigr) + ε \end{array}
雑に示すことができます。
(詳細はカラテオドリ外測度の記事で)
コルモゴロフの拡張定理 Kolmogorov
|| 直積は無限回しても測度空間になる
「測度である」が崩れない条件の1つ
\begin{array}{lcc} μ_X\times μ_Y &&〇 \\ \\ μ_X\times μ_Y \times μ_Z &&〇 \\ \\ μ_{X_1} \times μ_{X_2} \times μ_{X_3} \times \cdots \times μ_{X_n} &&〇 \\ \\ μ_{X_1} \times μ_{X_2} \times μ_{X_3} \times \cdots \times μ_{X_n} \times \cdots &&\textcolor{pink}{〇} \end{array}
↑ の話を考えると
「直積」を「有限回」行っても
「測度空間」は「測度空間」のままですが
\begin{array}{ccc} μ_{X_1} \times μ_{X_2} \times μ_{X_3} \times \cdots \times μ_{X_n} \times \cdots \end{array}
「無限回」行ってもそのままかは
この時点では分かっていません。
まあ結論から言えば
「無限直積測度空間」は
ある条件の元で「測度空間」になるんですが
\begin{array}{ccc} \displaystyle \left( \prod_{n=1}^{\infty}X_n , \bigotimes_{n=1}^{\infty}σ_{X_{n}} , \prod_{n=1}^{\infty}μ_{X_n} \right) \\ \\ (X^{\infty} , σ_X^{\infty} , μ^{\infty} ) \\ \\ (R^{\infty} , \mathrm{Borel}(R^{\infty}) , μ^{\infty} ) \end{array}
これについては
長くなるので詳しくは別の記事でやります。
