|| ある範囲内に変化量が 0 の点が1個はある
平均値の定理の証明に必要になるやつ
スポンサーリンク
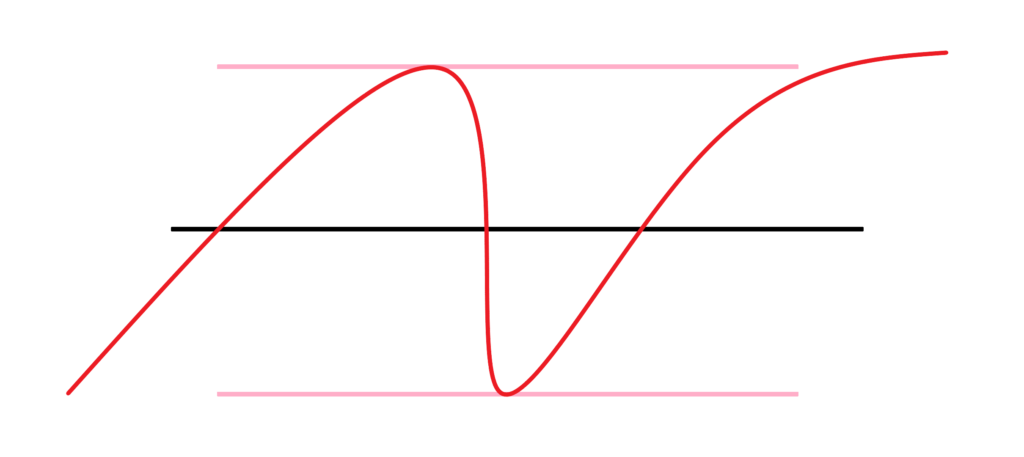
赤線 f(x) と黒線 y=k の交点 f(a)=f(b)=k
この a≤x≤b の間にピンクの線があるよ。
これがこの定理の主張になります。
厳密な言い回し
区間 [a,b] で連続
(a,b) で微分可能な関数 f(x) について
\begin{array}{llllll} \displaystyle f(a)&=&f(b) \end{array}
\begin{array}{llllll} \displaystyle a&<&c&<&b \end{array}
\begin{array}{llllll} \displaystyle f^{\prime}(c) &=& 0 \end{array}
区間 [a,b] 内にこういう c が存在する。
証明
線 f(x) は区間 [a,b] 内で連続な関数で
f(a_0)=f(b_0)=k であるとします。
\begin{array}{llllll} \displaystyle f(x)-f(a_0) \\ \\ f(b_0)-f(a_0)&=&0 \end{array}
ここで計算・イメージの簡略化のため
図形を f(a_0) だけ y 軸を平行移動させることで
f(a)=f(b)=0 である、ともしておきます。
\begin{array}{llllll} \displaystyle \mathrm{Case}2 && ∃x_+ &f(x_+)&>&0 \\ \\ \mathrm{Case}1 &&∀x &f(x)&=&0 \\ \\ \mathrm{Case}3 && ∃x_-&f(x_-)&<&0 \end{array}
その上で証明するにあたり
線の「形」によって話が変わるので
この3つのパターンに場合分けして考えます。
\begin{array}{llllll} \displaystyle ∃x_+ &f(x_+)&>&0 \end{array}
ちなみにこの「 ∃x \,\, A 」という記号は
「条件 A を満たす x が存在する」って意味です。
\begin{array}{llllll} \displaystyle \mathrm{Case}2 && ∃x_+ &f(x_+)&>&k \\ \\ \mathrm{Case}1 &&∀x &f(x)&=&k \\ \\ \mathrm{Case}3 && ∃x_-&f(x_-)&<&k \end{array}
ちなみに f(a_0)=f(b_0)=k で考える場合
パターンの場合分けはこうなります。
Case1. f(x)=0
語るまでもないパターンではありますが
f(x)=0 である以上
\begin{array}{llllll} \displaystyle f^{\prime}(x) &=&\displaystyle\frac{d}{dx}f(x) \\ \\ &=&\displaystyle\frac{d}{dx} 0 \\ \\ &=&0 \end{array}
当然「区間 [a,b] 」内の点はこう
つまり「全ての点は f^{\prime}(x)=0 を満たす」ので
\begin{array}{cccccccccc} \displaystyle a&<&c&<&b \\ \\ f(a)&=&f(c)&=&f(b)&=&0 \end{array}
\begin{array}{llllll} \displaystyle f^{\prime}(x) &=&0 \\ \\ &=&f^{\prime}(c) \end{array}
区間 [a,b] 内にこういった点 c は確実に存在します。
Case2. 区間 [a,b] 内で ∃x_+ \, f(x_+)>0
これは「 f(x)=0 ではない線」という
大まかな範囲を考えるための話です。
\begin{array}{llllll} \displaystyle \mathrm{Case}2 && ∃x_+ &f(x_+)&>&0 \\ \\ \mathrm{Case}3 && ∃x_-&f(x_-)&<&0 \end{array}
線 f(x) が 0 より上の点 x_+ を持つ場合
以下の広い範囲をカバーすることができます。
\begin{array}{llllll} \displaystyle f(x)&>&0 &&〇 \\ \\ f(x)&≥&0 &&〇 \\ \\ f(x_+)&>&0 && 〇 \\ \\ f(x_-)&<&0 && △ \\ \\ f(x)&≤&0 &&× \\ \\ f(x)&<&0 &&× \end{array}
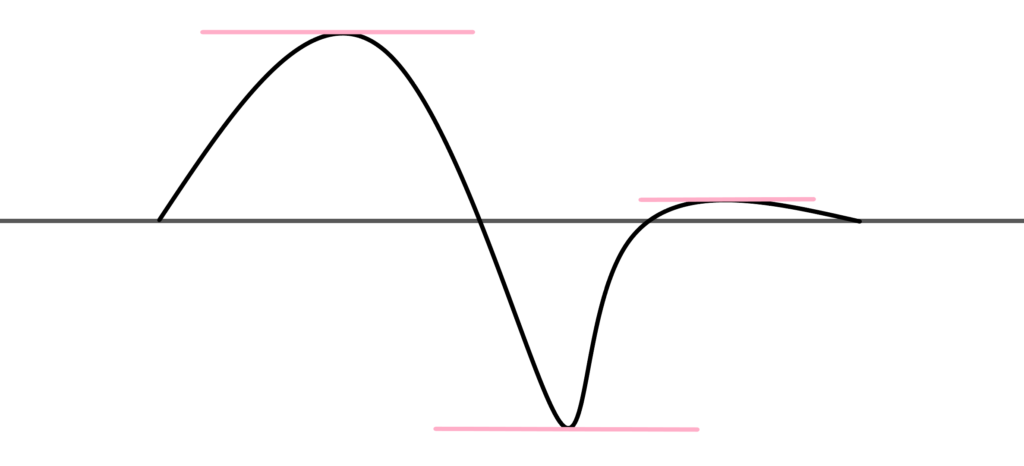
ただ f(x_-)<0 となる点 x_- を持つ f(x)
この範囲はカバーできないので
また別に考える必要はありますが
\begin{array}{llllll} \displaystyle a&≤&x_+&≤&b \end{array}
とりあえず計算しやすいので f(x_+)>0 から考えていきます。
まず「最大値最小値の定理(詳細は後で)」から
f(x) は「区間 [a,b] 内で連続な関数」であるため
\begin{array}{llllll} \displaystyle f(x)&≤&f(c) &&a≤c≤b \end{array}
最大値 f(c) は存在し
その点 c もまた存在する、と言えます。
\begin{array}{llllll} \displaystyle 0&<&f(x_+)&<&f(c) \end{array}
そして f(x_+)>0 となる x_+ が存在する以上
これもまた確実なこととして導かれます。
\begin{array}{llllll} \displaystyle f(a)&=&f(b)&=&0&<&f(c) \end{array}
\begin{array}{llllll} \displaystyle c&≠&a \\ \\ c&≠&b \end{array}
ということは確実にこうなるため
\begin{array}{llllll} \displaystyle a&<&c&<&b \end{array}
確実にこうなることが分かります。
f^{\prime}(c)=0 であることを示す
定理の内容自体は明らか
つまりゴールは見えているので
\begin{array}{llllll} \displaystyle f(x)-f(c)&≤&0 \end{array}
「 f(c) が最大値」である点
そして x<c の範囲と c<x の範囲から
f^{\prime}(c)=0 を導いてみます。
\begin{array}{llllll} 0&≤&\displaystyle \lim_{x\to c-0}\frac{f(x)-f(c)}{x-c} && && (x<c) \\ \\ &&\displaystyle \lim_{x\to c+0}\frac{f(x)-f(c)}{x-c} &≤&0 && (c<x) \end{array}
右極限と左極限をとってみればこれは明らか。
\begin{array}{llllll} \displaystyle 0&≤&\displaystyle \lim_{x\to c}\frac{f(x)-f(c)}{x-c} &≤&0 \end{array}
つまりこうなるので
\begin{array}{llllll} \displaystyle f^{\prime}(c)&=&\displaystyle \lim_{h\to 0}\frac{f(c+h)-f(c)}{(c+h)-c} \\ \\ &=&\displaystyle \lim_{x-c\to 0}\frac{f(c+x-c)-f(c)}{(c+x-c)-c} \\ \\ &=&\displaystyle \lim_{x-c\to 0}\frac{f(x)-f(c)}{x-c} \\ \\ &=&\displaystyle \lim_{x\to c}\frac{f(x)-f(c)}{x-c} \end{array}
微分の定義を整理しておくとこうですから
\begin{array}{llllll} \displaystyle f^{\prime}(c)&=&\displaystyle \lim_{x\to c}\frac{f(x)-f(c)}{x-c} \\ \\ &=&0 \end{array}
確実にこのようになると言えます。
Case3. 区間 [a,b] 内で ∃x_- \, f(x_-)<0
f(x_+)>0 のパターンとほぼ同様の内容になるので
このパターンは式だけ書いておきます。
\begin{array}{llllll} \displaystyle f(c)&≤&f(x) &&a≤c≤b \end{array}
\begin{array}{llllll} \displaystyle f(c)&<&f(x_-)&<&0 \end{array}
\begin{array}{llllll} \displaystyle f(c)&<&0&=&f(a)&=&f(b) \end{array}
\begin{array}{llllll} \displaystyle c&≠&a \\ \\ c&≠&b \end{array}
\begin{array}{llllll} \displaystyle a&<&c&<&b \end{array}
微分についても符号が変わるだけ
\begin{array}{llllll} \displaystyle 0&≤&f(x)-f(c) \end{array}
\begin{array}{llllll} &&\displaystyle \lim_{x\to -c}\frac{f(x)-f(c)}{x-c} &≤&0 && (x<c) \\ \\ 0&≤&\displaystyle \lim_{x\to +c}\frac{f(x)-f(c)}{x-c} && && (c<x) \end{array}
以上、このパターンはこんな感じです。
まとめ
線 f(x) は区間 [a,b] 内で連続な関数で
f(a_0)=f(b_0)=0 であるとする
\begin{array}{llllll} \displaystyle f^{\prime}(c)=0 && a<c<b \end{array}
すると以下の全パターンで ↑ になるような
そういう点 c が存在する。
\begin{array}{llllll} \displaystyle \mathrm{Case}2 && ∃x_+ &f(x_+)&>&0 &&〇 \\ \\ \mathrm{Case}1 &&∀x &f(x)&=&0 && 〇\\ \\ \mathrm{Case}3 && ∃x_-&f(x_-)&<&0 && 〇 \end{array}
以上、証明終わり
