|| ルベーグ積分の基礎になる主張
単関数で積分ができる感じ
スポンサーリンク
この定理の厳密な主張は以下の通りです。
\begin{array}{llllll} \displaystyle |f_n(x)|&≤&|f_{n+1}(x)|&≤&|f(x)| \end{array}
この条件を満たす
「単関数列 f_1(x),f_2(x),...,f_n(x),... 」が存在する
目次
可測関数「要するに普通の関数のこと」
単関数「互いに素な定義関数の和」
定義関数「それかそれ以外か」
近似定理の感覚「ずっと増えて限界がある → 限界に到達」
近似定理の証明「都合の良い操作を考える」
都合の良い関数「ある関数に寄る単関数列」
可測関数 Measurable Function
|| 全ての普通の関数のこと
「ルベーグ可測」な関数のことで
\begin{array}{llllll} \displaystyle (X,σ_X)&→&(Y,σ_Y) \end{array}
\begin{array}{llllll} \displaystyle f&:&X&\to&Y \\ \\ f^{-1}&:&X&←&Y \end{array}
\begin{array}{cclllllll} \displaystyle D&∈&σ_Y &&\to&& f^{-1}(D)&∈&σ_X \end{array}
ほぼ全ての関数はこれに含まれます。
含まれないやつはかなり特殊です。
具体的には
定義関数 Indicator Function
|| リーマン積分不可の関数を簡単に作れる
かなり実用性のある関数で
\begin{array}{rcl} \displaystyle 1_D(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈D \\ \\ 0 &&x∉D \end{array} \right. \\ \\ \\ \displaystyle χ_P(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&P(x)\,\,\mathrm{is} \,\, \mathrm{True} \\ \\ 0 &&P(x) \,\,\mathrm{is} \,\, \mathrm{False} \end{array} \right. \end{array}
条件を狭める時とか
他にもいろんな場面でよく使います。
補足しておくと
\begin{array}{cccllllll} \displaystyle \int_{-\infty}^{\infty}1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} \,dx \\ \\ \displaystyle \int_{-\infty}^{\infty}f(x)1_{[0,1]}(x)\,dx &=&\displaystyle \int_{0}^{1} f(x) \,dx \end{array}
定義関数はこういう性質を持っています。
単関数 Simple Function
|| 定義関数の性質から導かれるやつ
関数を足し算の集まりに変換できる
\begin{array}{llllll} \displaystyle φ(x)&=&\displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \end{array}
以下の性質から導かれます。
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle φ(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
\begin{array}{cllllll} \displaystyle a_1 1_{D_1}(x) \\ \\ a_2 1_{D_2}(x) \\ \\ \vdots \\ \\ a_n 1_{D_n}(x) \end{array}
\begin{array}{llllll} \displaystyle μ \left( \displaystyle\sum_{k=1}^{n}a_k 1_{D_k}(x) \right)&=&\displaystyle μ\Bigl( a_1 1_{D_1}(x)\Bigr) +\cdots + μ\Bigl( a_n 1_{D_n}(x)\Bigr) \end{array}
記号がややこしいですが
よく見ると当たり前の話しかしてません。
単関数の積分
これはその雛型とも言えるもので
\begin{array}{llllll} \displaystyle \left( \begin{array}{cccllllll} \displaystyle i≠j \\ \\ ↓ \\ \\ D_i∩D_j=∅ \end{array} \right)&&→&&\displaystyle φ(x)&=&\displaystyle \left\{ \begin{array}{lcl} \displaystyle a_1&&x∈D_1 \\ \\ a_2 &&x∈D_2 \\ \\ &\vdots \\ \\ a_n &&x∈D_n \\ \\ 0&&\mathrm{Otherwise} \end{array} \right. \end{array}
この前提のもと
\begin{array}{llllll} \displaystyle D &=&\displaystyle \bigcup_{k=1}^{n}D_k \\ \\ &=&\displaystyle D_1∪D_2∪ \cdots ∪D_n \end{array}
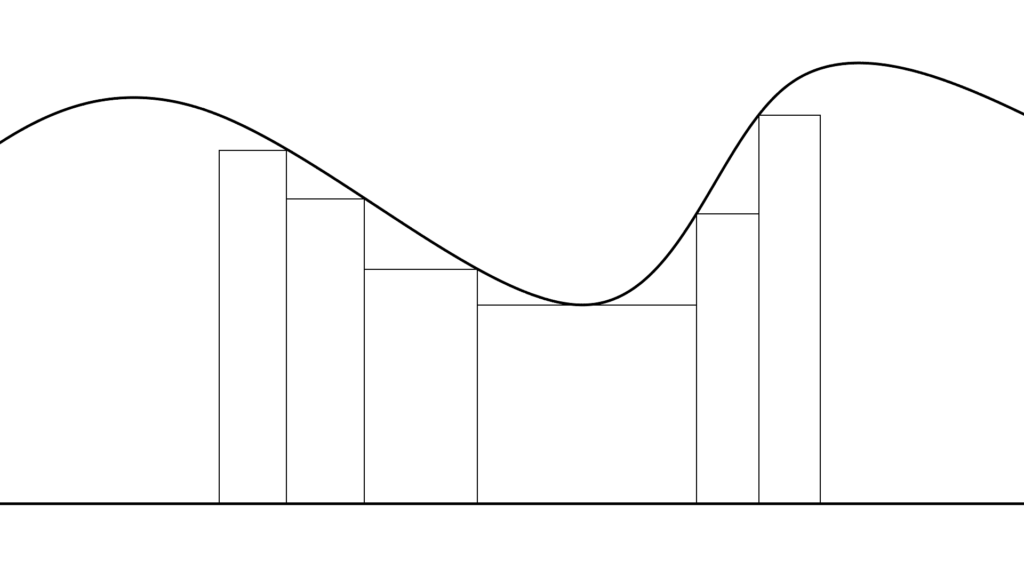
\begin{array}{llllll} \displaystyle \int_{D} φ(x) \, μ(dx) &=&\displaystyle\sum_{k=1}^{n}a_k \, μ(D_k) \end{array}
\begin{array}{llllll} \displaystyle μ(dx)&=&μ(D_k) \\ \\ μ(dx)&=&μ([x_{k-1},x_k]) \\ \\ &=&x_k-x_{k-1} \end{array}
「単関数の積分」は
このような形で定義されていて
\begin{array}{llllll} \displaystyle \int_{D}f(x) \,dx \end{array}
これが『積分値の近似』で使われる
「内測度」「外測度」の具体的な中身になります。
単関数近似定理の感覚
直感的な話をするために
f(x) は「非負値可測関数」
φ_n(x) は「 n が増えると単調増加」する「単関数」
このように定めると
この定理の主張は
「リーマン積分」的な感覚で理解することができます。

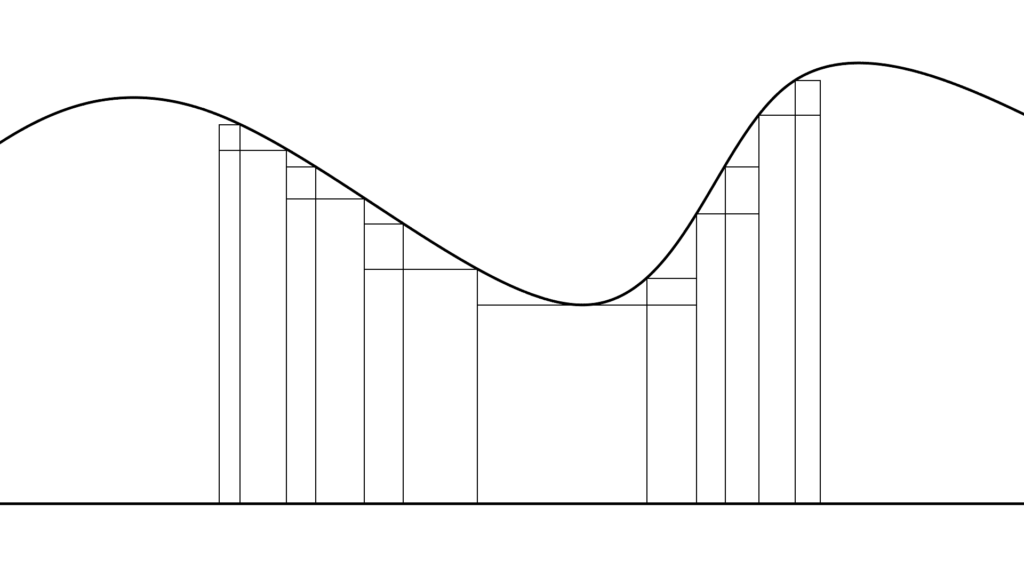
ちなみに「単調増加する単関数」ってのは
具体的にはこんな感じです。
\begin{array}{llllll} \displaystyle φ_n(x)&≤&f(x) \end{array}
この前提のもと
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} φ_n(x)&=&\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}a_k 1_{D_k}(x) \end{array}
このようにすると
「単調増加する」以上
\begin{array}{llllll} \displaystyle φ_n(x)&≤&φ_{n+1}(x)&≤&f(x) \end{array}
n を増やせば
最後には必ず「上限 f(x) 」に到達するので
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}a_k 1_{D_k}(x)&=&f(x) \end{array}
これが f(x) に近似するというのは
わりと直感的に分かると思います。
近似定理の証明
この近似定理の最大の問題点
それは
\begin{array}{llllll} \displaystyle 0&≤&|f_n(x)|&≤&|f(x)| \end{array}
単関数 f_n(x) 列の上限に f(x) が来ること
\begin{array}{llllll} \displaystyle |f_n(x)|&≤&|f_{n+1}(x)| \end{array}
単関数が単調増加すること
これらの条件を満たすような
そんな都合の良い関数は本当に存在するのか
存在したとして
一意に定めることができるのか
そういった点で、
この定理の証明の内容は
だいたいその辺りの話がメインになります。
具体例から逆算してみる
↑ で話したように
「非負値可測関数」「単調増加」
\begin{array}{llllll} \displaystyle 0&≤&f_n(x)&≤&f_{n+1}(x)&≤&f(x) \end{array}
この条件で近似していくのは
直感的に明らかです。
どう考えても寄っていきます。

なのでとりあえず
まずはこの条件から
具体的な関数の形を考えていくことにします。
均等に分割していく
まずは短絡的に
f(x) に近似していく単関数を
均等に分けて考えてみます。
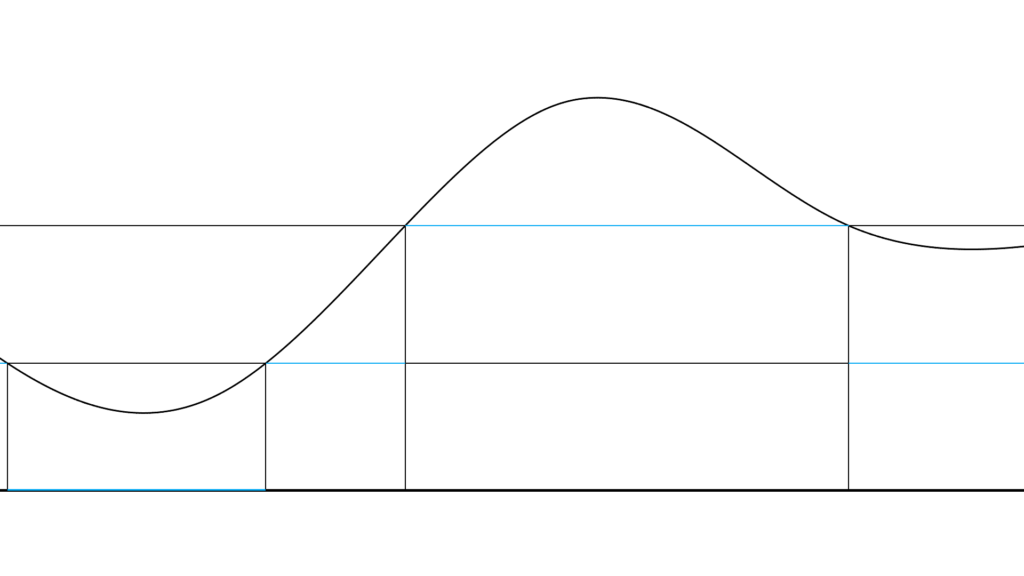
\begin{array}{llllll} \displaystyle f_1(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle 0 &&\displaystyle 0≤f(x)<\frac{1}{2} \\ \\ \displaystyle \frac{1}{2} &&\displaystyle \frac{1}{2}≤f(x)<1 \\ \\ 1 &&\displaystyle 1≤f(x) \end{array} \right. \end{array}
するとこんな感じに分けられて
(半分じゃなくても良い)
\begin{array}{llllll} \displaystyle f_2(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle 0 &&\displaystyle 0≤f(x)<\frac{1}{4} \\ \\ \displaystyle \frac{1}{4} &&\displaystyle \frac{1}{4}≤f(x)<\frac{2}{4} \\ \\ \displaystyle \frac{2}{4} &&\displaystyle \frac{2}{4}≤f(x)<\frac{3}{4} \\ \\ \displaystyle \frac{3}{4} &&\displaystyle \frac{3}{4}≤f(x)<\frac{4}{4} \\ \\ 1 &&\displaystyle 1≤f(x) \end{array} \right. \end{array}
以下、同様の操作が行えます。
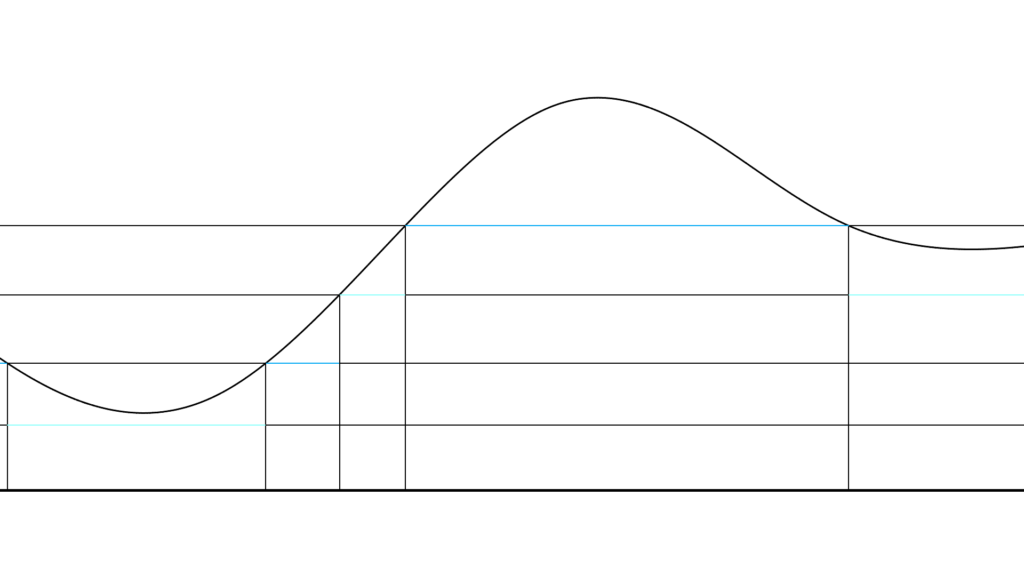
半々にしていけばどこまでも細かくできるので
こうすれば f(x)≤1 だったら近似できます。
(この時点で単調増加なのは直感的には明らか)
しかし 1<f(x) の場合では
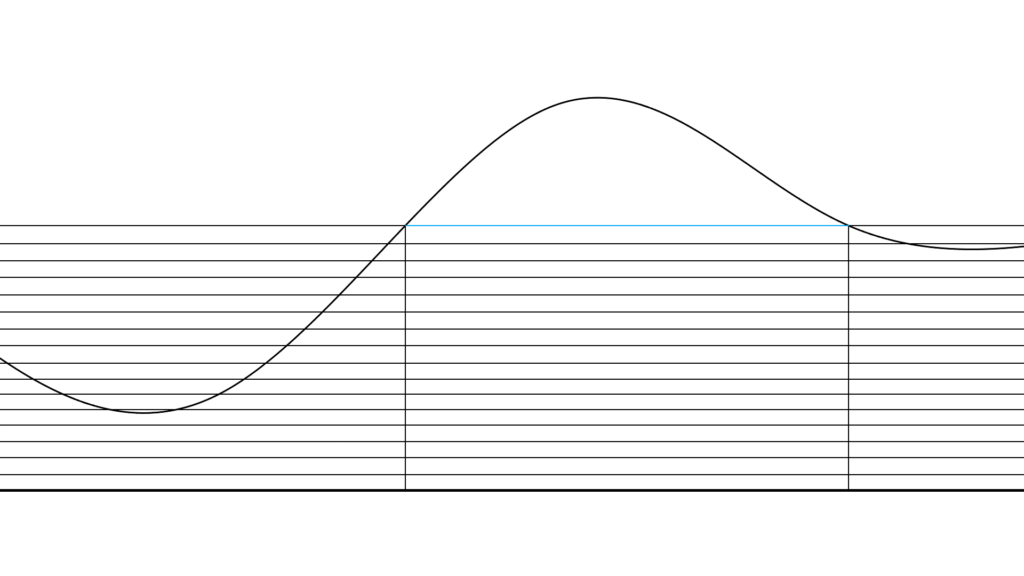
0≤f(x)≤1 の範囲しか細かくできないので
どうしても近似できない部分ができてしまいます。
単純に分割するだけじゃ足りない
0≤f(x)≤1 の範囲だけではなく
\begin{array}{llllll} \displaystyle f_2(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle 0 &&\displaystyle 0≤f(x)<\frac{1}{4} \\ \\ \displaystyle \frac{1}{4} &&\displaystyle \frac{1}{4}≤f(x)<\frac{2}{4} \\ \\ \displaystyle \frac{2}{4} &&\displaystyle \frac{2}{4}≤f(x)<\frac{3}{4} \\ \\ \displaystyle \frac{3}{4} &&\displaystyle \frac{3}{4}≤f(x)<\frac{4}{4} \\ \\ 1 &&\displaystyle 1≤f(x) \end{array} \right. \end{array}
1<f(x) の方向にも拡張する
\begin{array}{llllll} \displaystyle f_2(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle 0 &&\displaystyle 0≤f(x)<\frac{1}{4} \\ \\ \displaystyle \frac{1}{4} &&\displaystyle \frac{1}{4}≤f(x)<\frac{2}{4} \\ \\ \displaystyle \frac{2}{4} &&\displaystyle \frac{2}{4}≤f(x)<\frac{3}{4} \\ \\ \displaystyle \frac{3}{4} &&\displaystyle \frac{3}{4}≤f(x)<\frac{4}{4} \\ \\ \displaystyle \frac{4}{4} &&\displaystyle \frac{4}{4}≤f(x)<\frac{5}{4} \\ \\ \displaystyle \frac{5}{4} &&\displaystyle \frac{5}{4}≤f(x)<\frac{6}{4} \\ \\ \displaystyle \frac{6}{4} &&\displaystyle \frac{6}{4}≤f(x)<\frac{7}{4} \\ \\ \displaystyle \frac{7}{4} &&\displaystyle \frac{7}{4}≤f(x)<\frac{8}{4} \\ \\ 2 &&\displaystyle 2≤f(x) \end{array} \right. \end{array}
そうしなければ近似できない可能性があるので
とりあえずこのようにしてみます。
( f(x)<n_+ の部分で該当する x は無し)
すると
\begin{array}{llllll} \displaystyle f_n(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle 0 &&\displaystyle 0≤f(x)<\frac{1}{2^n} \\ \\ \displaystyle \frac{1}{2^n} &&\displaystyle \frac{1}{2^n}≤f(x)<\frac{2}{2^n} \\ \\ \displaystyle \frac{2}{2^n} &&\displaystyle \frac{2}{2^n}≤f(x)<\frac{3}{2^n} \\ \\ \displaystyle \frac{3}{2^n} &&\displaystyle \frac{3}{2^n}≤f(x)<\frac{4}{2^n} \\ \\ &\vdots \\ \\ \displaystyle n-\frac{1}{2^n} &&\displaystyle n-\frac{1}{2^n}≤f(x)<\frac{n2^n}{2^n} \\ \\ n &&\displaystyle n≤f(x) \end{array} \right. \end{array}
この操作はこんな感じに一般化できるので
この時点で
なんか都合の良さそうな関数が出来上がります。
都合の良さそうな関数
良い感じの関数が導けたので
「単調増加する」かどうか
\begin{array}{llllll} \displaystyle k&∈&\{0,1,2,3,4,5,...,n2^n-1\} \end{array}
\begin{array}{llllll} \displaystyle f_n(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle \frac{k}{2^n} &&\displaystyle \frac{k}{2^n}≤f(x)<\frac{k+1}{2^n} \\ \\ n &&\displaystyle n≤f(x) \end{array} \right. \end{array}
そして「 f(x) に収束する」かどうか
この辺りを改めて確認していきます。
f_n は単調増加する
これは直感的に明らかですが
念のため、きちんと確認しておきます。
\begin{array}{llllll} f_n(x)&=&\displaystyle \frac{k}{2^n} \end{array}
\begin{array}{llllll} 0&≤&\displaystyle f_{n+1}(x)-f_n(x) \end{array}
着地はここで
\begin{array}{llllll} \displaystyle \frac{k}{2^n}&≤&f(x)&<&\displaystyle\frac{k+1}{2^n} \end{array}
↓
\begin{array}{llllll} \displaystyle \frac{k}{2^n}&≤&f(x)&<&\displaystyle\frac{k+\frac{1}{2}}{2^n} &&\displaystyle \frac{k+\frac{1}{2}}{2^n}&≤&f(x)&<&\displaystyle\frac{k+1}{2^n} \end{array}
n+1 では範囲が分割され
それに伴って分割する数 k も増えていることから
\begin{array}{llllll} \displaystyle \frac{k}{2^n}≤f(x)<\displaystyle\frac{k+\frac{1}{2}}{2^n} &&\displaystyle \frac{k+\frac{1}{2}}{2^n}≤f(x)<\displaystyle\frac{k+1}{2^n} \end{array}
\begin{array}{llllll} \displaystyle \times \frac{2}{2} \end{array}
\begin{array}{llllll} \displaystyle \frac{2k}{2^{n+1}}≤f(x)<\displaystyle\frac{2k+1}{2^{n+1}} &&\displaystyle \frac{2k+1}{2^{n+1}}≤f(x)<\displaystyle\frac{2(k+1)}{2^{n+1}} \end{array}
同じ範囲を比較するとこうですから
\begin{array}{llllll} \displaystyle \frac{k}{2^n}&≤&f(x)&<&\displaystyle\frac{k+\frac{1}{2}}{2^n} \end{array}
↓
\begin{array}{llllll} \displaystyle f_{n+1}(x)-f_n(x)&=&\displaystyle \frac{2k}{2^{n+1}}-\frac{k}{2^n} \\ \\ &=&\displaystyle \frac{2k}{2^{n+1}}-\frac{2k}{2^{n+1}} \\ \\ &=&0 \end{array}
この範囲だと当然こうなり
\begin{array}{llllll} \displaystyle \frac{k}{2^n}&≤&\displaystyle \frac{k+\frac{1}{2}}{2^n}&≤&f(x)&<&\displaystyle\frac{k+1}{2^n} \end{array}
↓
\begin{array}{llllll} \displaystyle f_{n+1}(x)-f_n(x)&=&\displaystyle \frac{2k+1}{2^{n+1}}-\frac{k}{2^n} \end{array}
前の結果より
\begin{array}{llllll} \displaystyle \frac{2k}{2^{n+1}}&≤&\displaystyle \frac{2k+1}{2^{n+1}} \end{array}
これが明らかですから
\begin{array}{llllll} 0&≤&\displaystyle f_{n+1}(x)-f_n(x) \end{array}
結果、こうなるので
間違いなく f_n(x) は単調増加すると言えます。
f(x) に収束するかどうか
こっちも直感的には明らかですが
f(x) が \infty になる場合とか
そういうのがあるのでちゃんと確認しておきます。
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}f_n(x)&=&f(x) \end{array}
というわけで
まず f(x)=\infty になる場合を確認しておくと
\begin{array}{llllll} \displaystyle n&≤&f(x)&=&\infty \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}f_n(x)&=&\displaystyle \lim_{n\to\infty}n &&n≤f(x) \\ \\ &=&\infty \end{array}
まあ当然ですがこうなって
f(x)<\infty の場合では
\begin{array}{llllll} \displaystyle f(x)-f_1(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle f(x)-0 &&\displaystyle 0≤f(x)<\frac{1}{2} \\ \\ \displaystyle f(x)-\frac{1}{2} &&\displaystyle \frac{1}{2}≤f(x)<1 \\ \\ f(x)-1 &&\displaystyle 1≤f(x) \end{array} \right. \end{array}
\begin{array}{llllll} \displaystyle f(x)-f_1(x)&≤&\displaystyle\frac{1}{2} &&f(x)<1 \end{array}
f(x) と f_n(x) の差は以下のようになるので
\begin{array}{llllll} \displaystyle f(x)-f_n(x)&≤&\displaystyle\frac{1}{2^n} &&f(x)<n \end{array}
n がどこまでも大きくなる
つまり『いずれ f(x) より大きくなる』以上
\infty 以外の点でも
\begin{array}{llllll} \displaystyle |f(x)-f_n(x)|&≤&\displaystyle\frac{1}{2^n} \end{array}
f_n(x) は f(x) に収束すると言えます。
非負値関数の単関数収束定理の証明
以上のことから
\begin{array}{llllll} \displaystyle k&∈&\{0,1,2,3,4,5,...,n2^n-1\} \end{array}
\begin{array}{llllll} \displaystyle f_n(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle \frac{k}{2^n} &&\displaystyle \frac{k}{2^n}≤f(x)<\frac{k+1}{2^n} \\ \\ n &&\displaystyle n≤f(x) \end{array} \right. \end{array}
このような単関数を定めると
これは「単調増加」であり
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} f_n(x)&=&f(x) \end{array}
f(x) に各点で収束するので
『 f(x) が非負の可測関数である』時
『関数 f に収束する単調増加列 \{f_n\} が存在する』
\begin{array}{llllll} \displaystyle f_n(x)&=&\displaystyle \left\{ \begin{array}{cccclll} \displaystyle \frac{k}{2^n} &&\displaystyle \frac{k}{2^n}≤f(x)<\frac{k+1}{2^n} \\ \\ n &&\displaystyle n≤f(x) \end{array} \right. \end{array}
結果として
この主張の正しさが示されました。
非負でない関数でも成立する
マイナスの値をとる場合でも
マイナス部分をプラスに加工すれば
\begin{array}{llllll} f(x)&→& \displaystyle |f(x)| \end{array}
非負可測関数の収束定理の話になるので
\begin{array}{llllll} \displaystyle f^+(x)&=&\displaystyle\left\{ \begin{array}{clllll} \displaystyle f(x) &&0<f(x) \\ \\ 0 && f(x)≤0 \end{array} \right. \\ \\ &=&\max\{ f(x),0 \} \\ \\ \\ \displaystyle f^-(x)&=&\displaystyle\left\{ \begin{array}{clllll} \displaystyle -f(x) &&f(x)<0 \\ \\ 0 && 0≤f(x) \end{array} \right. \\ \\ &=&\max\{ -f(x),0 \} \\ \\ &=&-\min\{ f(x),0 \} \end{array}
「正成分 f^+ 」「負成分 f^- 」
というものを考えて
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} f^+_n(x) &=& \displaystyle f^+(x) \\ \\ \displaystyle \lim_{n\to\infty} f^-_n(x) &=& \displaystyle f^-(x) \end{array}
その単関数を定義すれば
\begin{array}{llllll} f(x)&=& \displaystyle f^+(x)-f^-(x) \\ \\ f_n(x)&=& \displaystyle f^+_n(x)-f^-_n(x) \end{array}
f(x) に収束する単関数 f_n(x) を
このような形で定義できます。
(この操作を行っても可測関数)
